今天我们来讲下最近比较博眼球的联邦学习。应该很多人听过但是始终都没懂啥是联邦学习?百度一下发现大篇文章都说可以用来解决数据孤岛,那它又是如何来解决数据孤岛问题的?对于联邦学习,大部分文章还都处于其学术分享会的报道阶段,并未详细介绍联邦学习的实现方法,难以理解其真容,本篇文章将从技术角度介绍联邦学习。
1、联邦学习的背景介绍
近年来人工智能可谓风风火火,掀起一波又一波浪潮,从人脸识别、活体检验发现刑事案件报警到阿尔法狗大战人类围棋手李世石、再到无人驾驶、以及已被普遍应用的精准营销,AI逐步进入人们生活的方方面面。当然也不免出现部分过度吹捧,导致对AI的误解--AI无所不能,既然这么好用,为啥我不能拿来用一下?在追逐AI的同时却忽略了一点,AI是靠数据来喂的,而且是大量优质数据。
现实生活中,除了少数巨头公司能够满足,绝大多数企业都存在数据量少,数据质量差的问题,不足以支撑人工智能技术的实现;同时国内外监管环境也在逐步加强数据保护,陆续出台相关政策,如欧盟最近引入 的新法案《通用数据保护条例》(GDPR),我国国家互联网信息办公室起草的《数据安全管理办法(征求意见稿)》,因此数据在安全合规的前提下自由流动,成了大势所趋;在用户和企业角度下,商业公司所拥有的数据往往都有巨大的潜在价值。两个公司甚至公司间的部门都要考虑利益的交换,往往这些机构不会提供各自数据与其他公司做与单的聚合,导致即使在同一个公司内,数据也往往以孤岛形式出现。
基于以上不足以支撑实现、不允许粗暴交换、不愿意贡献价值三点,导致了现在大量存在的数据孤岛,以及隐私保护问题,联邦学习应运而生。
2、联邦学习的概念
本质:联邦学习本质上是一种分布式机器学习技术,或机器学习框架。
目标:联邦学习的目标是在保证数据隐私安全及合法合规的基础上,实现共同建模,提升AI模型的效果。
前身:联邦学习最早在 2016 年由谷歌提出,原本用于解决安卓手机终端用户在本地更新模型的问题;
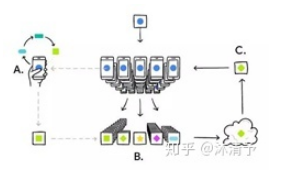
3、联邦学习的分类
我们把每个参与共同建模的企业称为参与方,根据多参与方之间数据分布的不同,把联邦学习分为三类:横向联邦学习、纵向联邦学习和联邦迁移学习。
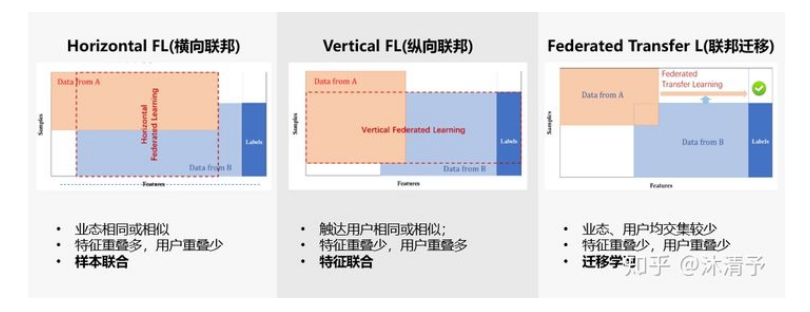

3.1 横向联邦学习
适用场景:
横向联邦学习的本质是样本的联合,适用于参与者间业态相同但触达客户不同,即特征重叠多,用户重叠少时的场景,比如不同地区的银行间,他们的业务相似(特征相似),但用户不同(样本不同)
学习过程:
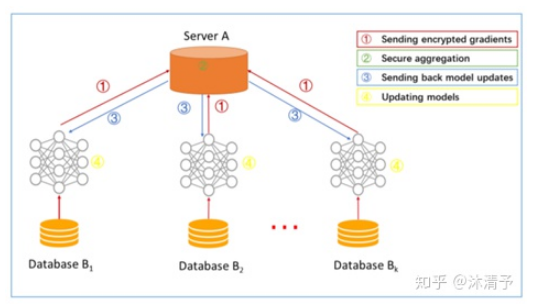
step1:参与方各自从服务器A下载最新模型;
step2:每个参与方利用本地数据训练模型,加密梯度上传给服务器A,服务器A聚合各用户的梯度更新模型参数;
step3:服务器A返回更新后的模型给各参与方;
step4:各参与方更新各自模型。
步骤解读:在传统的机器学习建模中,通常是把模型训练需要的数据集合到一个数据中心然后再训练模型,之后预测。在横向联邦学习中,可以看作是基于样本的分布式模型训练,分发全部数据到不同的机器,每台机器从服务器下载模型,然后利用本地数据训练模型,之后返回给服务器需要更新的参数;服务器聚合各机器上的返回的参数,更新模型,再把最新的模型反馈到每台机器。
在这个过程中,每台机器下都是相同且完整的模型,且机器之间不交流不依赖,在预测时每台机器也可以独立预测,可以把这个过程看作成基于样本的分布式模型训练。谷歌最初就是采用横向联邦的方式解决安卓手机终端用户在本地更新模型的问题的。
3.2 纵向联邦学习
适用场景:
纵向联邦学习的本质是特征的联合,适用于用户重叠多,特征重叠少的场景,比如同一地区的商超和银行,他们触达的用户都为该地区的居民(样本相同),但业务不同(特征不同)。
学习过程:
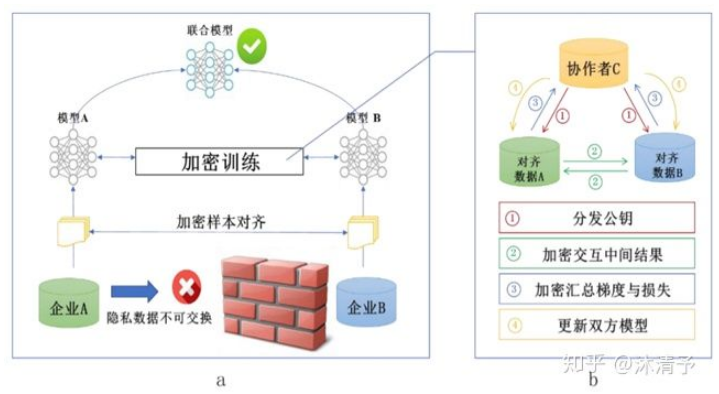
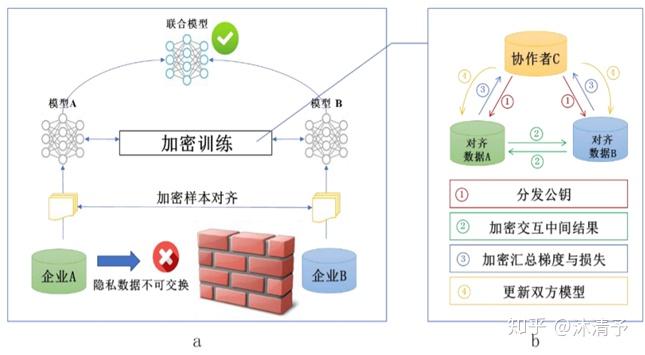 纵向联邦学习的本质是交叉用户在不同业态下的特征联合,比如商超A和银行B,在传统的机器学习建模过程中,需要将两部分数据集中到一个数据中心,然后再将每个用户的特征join成一条数据用来训练模型,所以就需要双方有用户交集(基于join结果建模),并有一方存在label。其学习步骤如上图所示,分为两大步:
纵向联邦学习的本质是交叉用户在不同业态下的特征联合,比如商超A和银行B,在传统的机器学习建模过程中,需要将两部分数据集中到一个数据中心,然后再将每个用户的特征join成一条数据用来训练模型,所以就需要双方有用户交集(基于join结果建模),并有一方存在label。其学习步骤如上图所示,分为两大步:第一步:加密样本对齐。是在系统级做这件事,因此在企业感知层面不会暴露非交叉用户。
第二步:对齐样本进行模型加密训练:
step1:由第三方C向A和B发送公钥,用来加密需要传输的数据;
step2:A和B分别计算和自己相关的特征中间结果,并加密交互,用来求得各自梯度和损失;
step3:A和B分别计算各自加密后的梯度并添加掩码发送给C,同时B计算加密后的损失发送给C;
step4:C解密梯度和损失后回传给A和B,A、B去除掩码并更新模型。
步骤解读:我们以线性回归为例具体说明其训练过程。
存在数据集
,A和B分别初始化模型参数
其目标函数为:
令: ,且对原目标函数同态加密后可表示为:
,
表示同态加密,
,
,
,
因此有 ,同理令
,
梯度可表示如下:
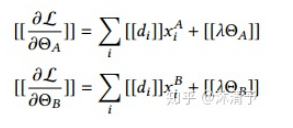
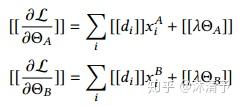
具体训练步骤如下:
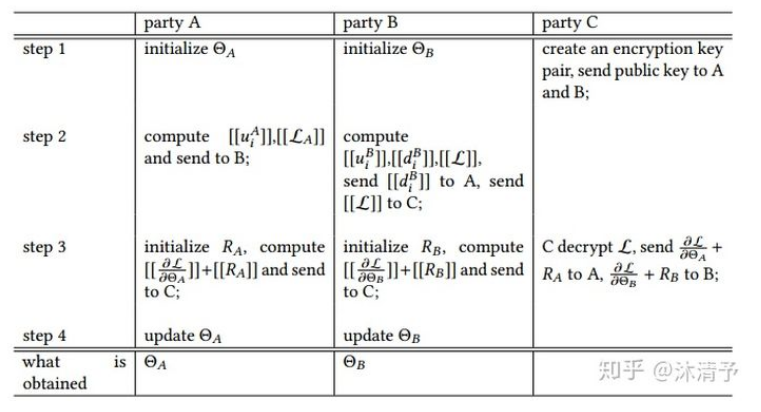
 在整个过程中参与方都不知道另一方的数据和特征,且训练结束后参与方只得到自己侧的模型参数,即半模型。
在整个过程中参与方都不知道另一方的数据和特征,且训练结束后参与方只得到自己侧的模型参数,即半模型。预测过程:
由于各参与方只能得到与自己相关的模型参数,预测时需要双方协作完成,如下图所示:
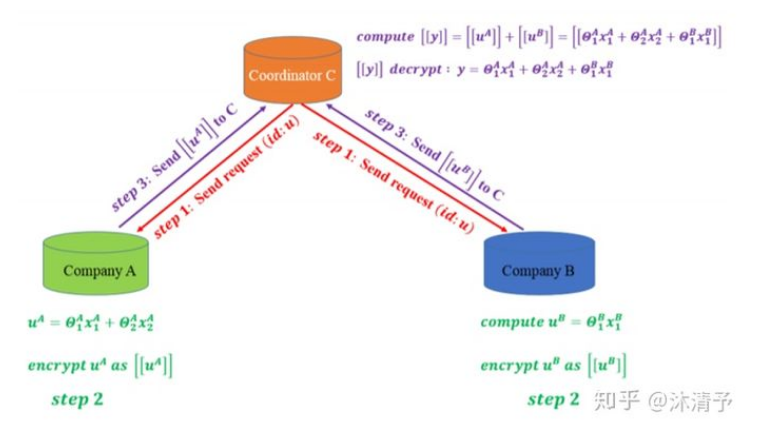

共同建模的结果:
- 双方均获得数据保护
- 共同提升模型效果
- 模型无损失
3.3 联邦迁移学习
适用场景:
当参与者间特征和样本重叠都很少时可以考虑使用联邦迁移学习,如不同地区的银行和商超间的联合。主要适用于以深度神经网络为基模型的场景。
迁移学习介绍:
迁移学习,是指利用数据、任务、或模型之间的相似性,将在源领域学习过的模型,应用于 目标领域的一种学习过程。
其实我们人类对于迁移学习这种能力,是与生俱来的。比如,我们如果已经会打乒乓球,就可以类比着学习打网球。再比如,我们如果已经会下中国象棋,就可以类比着下国际象棋。因为这些活动之间,往往有着极高的相似性。生活中常用的“举一反三”、“照猫画虎”就很好地体现了迁移学习的思想。

 迁移学习的核心是,找到源领域和目标领域之间的相似性,举一个杨强教授经常举的例子来说明:我们都知道在中国大陆开车时,驾驶员坐在左边,靠马路右侧行驶。这是基本的规则。然而,如果在英国、香港等地区开车,驾驶员是坐在右边,需要靠马路左侧行驶。那么,如果我们从中国大陆到了香港,应该如何快速地适应 他们的开车方式呢?诀窍就是找到这里的不变量:不论在哪个地区,驾驶员都是紧靠马路中间。这就是我们这个开车问题中的不变量。 找到相似性 (不变量),是进行迁移学习的核心。
迁移学习的核心是,找到源领域和目标领域之间的相似性,举一个杨强教授经常举的例子来说明:我们都知道在中国大陆开车时,驾驶员坐在左边,靠马路右侧行驶。这是基本的规则。然而,如果在英国、香港等地区开车,驾驶员是坐在右边,需要靠马路左侧行驶。那么,如果我们从中国大陆到了香港,应该如何快速地适应 他们的开车方式呢?诀窍就是找到这里的不变量:不论在哪个地区,驾驶员都是紧靠马路中间。这就是我们这个开车问题中的不变量。 找到相似性 (不变量),是进行迁移学习的核心。学习过程:
联邦迁移学习的步骤与纵向联邦学习相似,只是中间传递结果不同(实际上每个模型的中间传递结果都不同)。这里重点讲一下联邦迁移的思想:
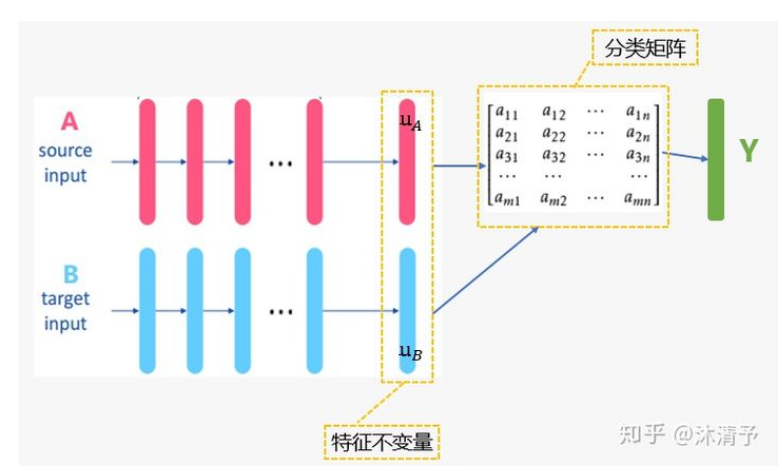
 源域:
源域: 目标函数:
整体目标函数为:
使用BP算法,根据目标函数 分别对
求梯度,双方交互计算梯度和损失需要用到的中间结果,重复迭代直至收敛。整个学习过程是利用A、B之间共同样本来学习两者间各自的特征不变量表示
,同时利用A的所有样本label
和A的不变量特征
学习分类器。在这个阶段中,[联邦] 体现在A,B可以通过安全交互中间结果共同学习一个模型,[迁移] 体现在B迁移了A的分类能力。在预测时,
依赖于 由
组成的分类器,因此和纵向联邦相同需要两者协作来完成。本节参考文章:Secure Federated Transfer Learning
最后,附上联邦学习开源github:https://github.com/webankfintech/fate
欢迎大家一起讨论!
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢