在之前的介绍中，我们对自监督学习（SSL）中的对比学习（CL）进行了简单介绍，然后针对对比学习中的采样方式进行详细的分析。由于对比学习的核心思想是在向量表征空间中将正样本（positive example）与锚点样本（anchor example）之间的距离拉近，将负样本（negative example）与锚点样本（anchor example）之间的距离拉远，因此，所选取的正负样本的质量直接决定了整个方法的效果。为此，有很多研究工作集中在对比学习的采样方法中，本文针对这些方法继续进行深挖，希望能够让大家对对比学习有更深入的认识，为大家带来一些微小的启发。

在接下来的介绍中，本文首先介绍了一个在自然语言中更巧妙使用数据增强的方法，避免了在 NLP 使用数据增强面临的数据质量的问题。接下来针对对比学习中的采样方式，分别从效率，假负样本更充分的利用，以及负样本难度的选择是如何影响模型效果的这几个方面进行简单介绍。

 

更好的自然语言处理样本生成（ConSERT ）[1]
在具体介绍针对正样本或者负样本的采样之前，首先介绍一个在自然语言处理中进行更好的数据增强的工作。该工作通过选择更合适的自然语言数据增强方法坍缩了 BERT 原生句子表示在表征空间存在的“坍缩”现象，同时也是一个标准的将对比学习应用在自然语言语义表征中的框架。
1.1 亮点

  1. 通过分析指出原生的 BERT 模型在句子语义表征中存在“坍缩”现象，即倾向于编码到一个较小的空间区域内，使大多数的句子对都具有较高的相似度分数，影响表征结果在具体下游任务中的表现

  2. 基于 BERT 模型提出了一种更好的对比学习方法，用于句子语义的表征

  3. 在监督实验，无监督实验，小样本实验中进行了充分的模型验证

1.2 方法

整体的模型框架图如下，相对于 BERT 模型而言思路非常简单，就是在输入到 encoder 的时候加了一个数据增强层。但作者进行了非常全面的考虑，例如为了避免直接从文本层面进行数据增强导致的语义变化问题，以及效率问题。作者提出直接在 embedding 层隐式生成数据增强样本，从而一方面避免以上问题，另一方面能够生成高质量的数据增强样本。

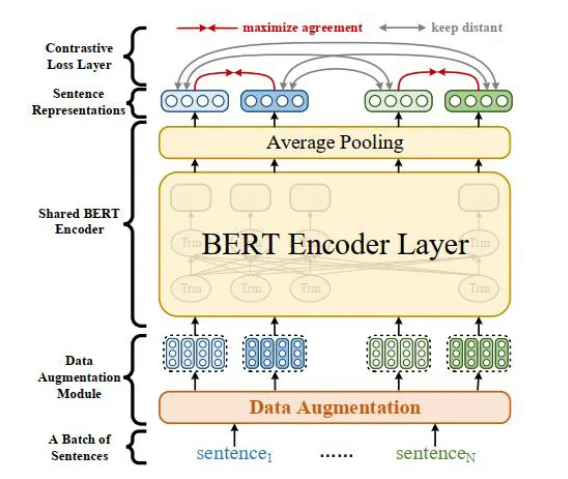
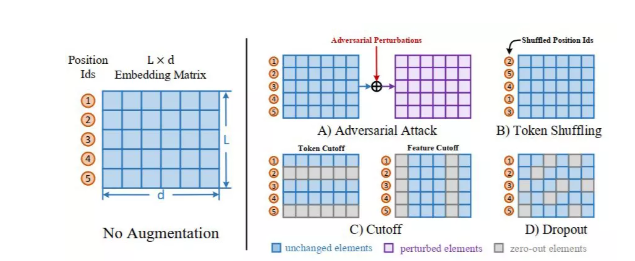
而在数据增强上，由于是在 embedding 层直接进行数据增强的，因此在这里作者选择了以下四种增强方式：

  1. 对抗攻击：通过梯度回传生成对抗扰动，将该扰动加到原本的 embedding 矩阵上

  2. 词序打乱：这个非常有意思，由于在 BERT 中是通过 position embedding 的方式显式指定位置的，因此直接将 position id 进行 shuffle 即可

  3. 裁剪：这部分分为两个粒度：a. 对某个 token 进行裁剪，直接将对应的 embedding 置为 0 即可，b. 对某些特征进行裁剪，即将 embedding 矩阵中对应列置为 0

  4. dropout：这个就是非常简单有效的方法了，直接利用 BERT 的结构进行 dropout 操作即可

     

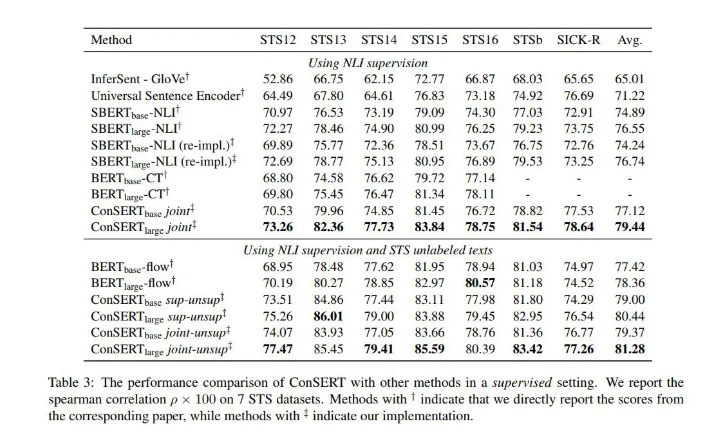
由于这些方法是直接面向 embedding 矩阵的，因此相对于显示生成增强文本的方法更为高效。针对本文的具体技术细节可以参考作者自己的解读。
1.3 实验

本文的实验也是非常充分的，作者处理利用对比学习框架进行无监督训练之外，还考虑了融合监督信号进行的增强训练，并提出了联合训练：有监督损失和无监督损失进行加权联合训练；现有监督在无监督：先用有监督损失训练模型，在利用无监督方法进行表示迁移；联合训练再无监督：先用联合损失训练模型，在无监督迁移。

以下展示了部分实验结果，从实验结果中可以看出模型的效果还是非常好的


个人认为本文最大的亮点就是对数据增强方法的利用，相对于 CV 领域的增强方法，NLP 领域的数据增强一直存在高质量的数据增强与原始语义的保证之间的矛盾。
本文通过直接在 embedding 矩阵上进行处理，一方面能够缓解以上矛盾，另一方面能够以一种更高效的方法进行，从而实现了 NLP 中更好的对比学习。这部分还可以参考 Mixup 这个工作，能够为这种方法提供更好的数据增强操作。

 

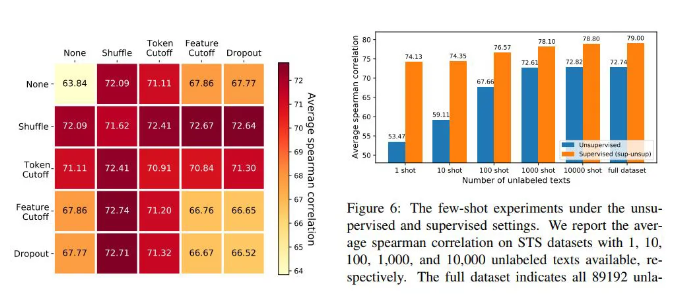
对比学习效率问题（Inefficiency of Self-supervised Representation Learning）[2]

在传统对比学习中，我们主要是通过以下方式进行对比，输入样本为锚点样本，数据增强样本为正样本，同一个 batch 中的其他样本默认为负样本。这种方法的好处是能够简单实现 1 个正样本 v.s. 多个负样本的学习，但问题也同样存在，这种方法本质上是一种实例级别的对比学习（Contrastive instance discrimination，或者 Instance-level contrastive learning），即每个样本都单独的一类。

本文通过实验发现，目前的这些方法效率比较低，比如需要 10 倍的 epoches 才能和监督学习有相似的效果。为了解决这种低效率的问题，作者开展了这个工作。

2.1 亮点

  1. 作者通过实验证明现有的对比学习方法效率低的原因有两个，under-clustering 和 over-clustering，前者是说在负样本数量不充足的时候很难学习到类别之间的不相似性；后者是说在实例级别的对比学习很难实现同一类样本的类内特征学习。

  2. 为了解决这种问题，作者提出了一种新的损失函数，将 infoNCE 替换为 triplet loss，以实现更多的负样本学习以及类内公共特征学习

2.2 方法

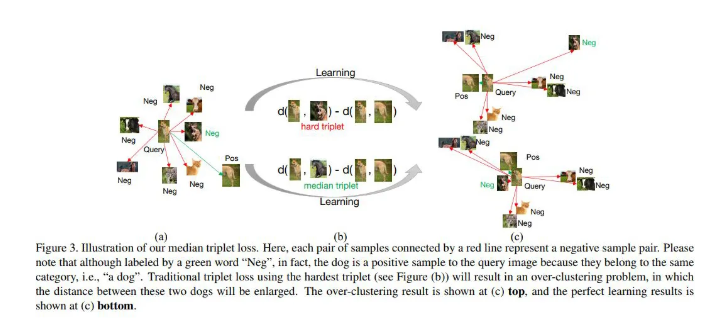
最主要的，作者提出了一种 Median Triplet Loss，在 triplet loss 的基础上进行了修正，以提升对比学习的效率和性能。以下是 median triplet loss 的一个直观图示：

首先普通的 triplet loss 可以表示为如下形式：

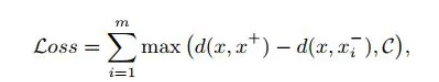
而为了提升 triplet loss 的效果，在实际应用中，一般会借鉴 SVM 的思想，直接选择最难的样本作为负样本进行损失计算，也即可以用如下形式表示：

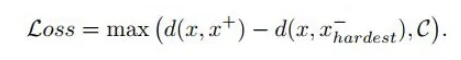
也就是说将 InfoNCE 损失替换为 triplet loss，并使用最难的样本进行计算的话，就可以解决 under-clustering 问题，因为最难的负样本都已经满足这个条件了，那其他所有的负样本也都会满足这个条件。

但这又会引出另一个问题，over-clustering 问题并没有得到解决，因为最难的样本是和锚点样本具有最大的语义相似度（负样本中），那么就有可能是假负样本，而这个假负样本性又是因为现在做的是实例级别的对比造成的。为了解决这个问题，作者想出来一个非常简单的方法，相对于对最难的样本做一个退化。

具体而言，既然最难的样本会造成 over-clustering 问题，但又想尽可能大的是使用决策边界，那是否可以降低一下难度呢？作者没有去解决假负样本的问题，而是说通过计算所有的负样本的难度，然后进行排序，选择中间的作为 triplet loss 的计算目标，这样一方面尽可能提升了负样本的难度（增大决策边界），另一方面缓解了 over-clustering 问题，因为使用的不是最难的负样本，这样，损失函数就变成了如下形式：

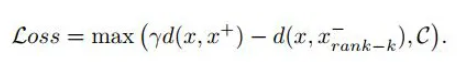
在计算难度的时候，作者选择了比较简单的余弦相似度去直接计算语义相似性。这部分作者并没有进行充分的研究分析。
2.3 实验

同样的，该方法也是一种通用的对比学习方法，为了验证其效果，作者在多个对比学习框架上进行了效果的验证，同时还对模型的效率进行了对比实验，从而验证模型提出的方法的有效性。部分实验结果如下图所示：

这篇文章最有意思的地方在于又使用回了 triplet loss，而且为了解决假负样本的问题，选择了一种非常简单的退化方法。思路非常简单，但实验结果证明了它非常有效。非常值得学习。

 

增量式负样本学习（Incremental False Negative）[3]
基于对比学习的基本思想，传统的对比学习大多是实例级别的对比，即每一个样本都是一类。这种方法在前一个工作中已经证明了效率非常低，在本文中，作者通过实验证明，这种方式忽略了不同样本之间的语义关系，而且采到的负样本对整个模型的影响还是很大的，为此。作者提出了一种增量式的假负样本检测识别方法。
3.1 亮点
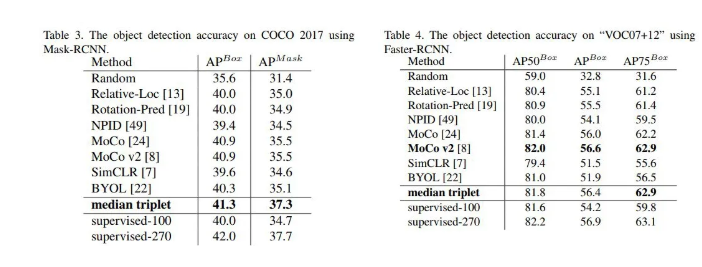
  1. 作者通过实验分析证明假负样本对整个对比学习的影响还是很大的，尤其是在大规模数据集上（数据量大，标签数量多）

  2. 本文提出了一种增量式的假负样本检测方法，按照置信度从高到低逐步移出假负样本，缓解假负样本对整个对比学习模型的影响。

3.2 方法

下图是整个模型的算法框架图，作者通过以一种增量学习的方式识别负样本采样中的假负样本，首先删除简单的假负样本，然后随着模型性能的提升，逐步删除难的假负样本，从而实现模型效果的提升

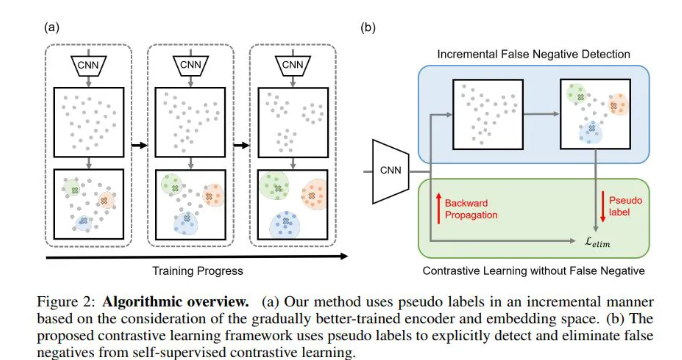
首先回顾一下传统对比学习的损失函数：

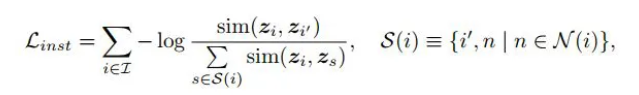
其中最主要的就是如何得到正确的正样本和负样本。在这里，作者主要关注于假负样本的检测。之前的方法，例如 DeepCluster，PCL 等大多是通过一次性的聚类得到伪标签，而这种方式是有些粗糙的。因为在刚开始的时候模型的建模能力是比较弱的，得到的输入表征的可信度也没有那么高。如果将这点考虑进来，就能够实现更好的假负样本检测。

为此，作者认为样本的标签应该满足一下条件：将样本赋予某一类别应该满足对应的表征不仅与对应的类别中心点近，而且应该和其他类别的中心点远。为此，作者提出了如下的置信度计算方法用于确定输入数据的伪标签：

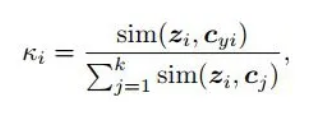
利用该计算公式，就能够为每一个负样本的伪标签添加上置信度，这样就可以设定接受阈值，当大于阈值时才会认为是真负样本，而且该置信度是利用学习到的表征进行计算的，因此它是和模型的性能直接相关的。因此能够动态的进行选择。

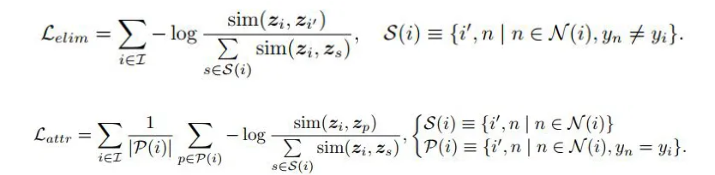
有了识别真负样本和假负样本的方法，作者针对损失函数进行了相对应的调整。一种是比较简单，直接将对应的假负样本删除即可，另一种是充分利用假负样本，既然是假负样本，那么它就是真正样本。将其加入到模型中进行对比学习，从而进一步提升对比学习的性能。两种损失函数的计算方法如下：

3.3 实验

由于作者提出的方法是一种通用的采样和对比学习方法， 作者在多个方法上进行了模型效果的验证，同时还验证了假负样本对整个模型的影响，相关实验结果如下：

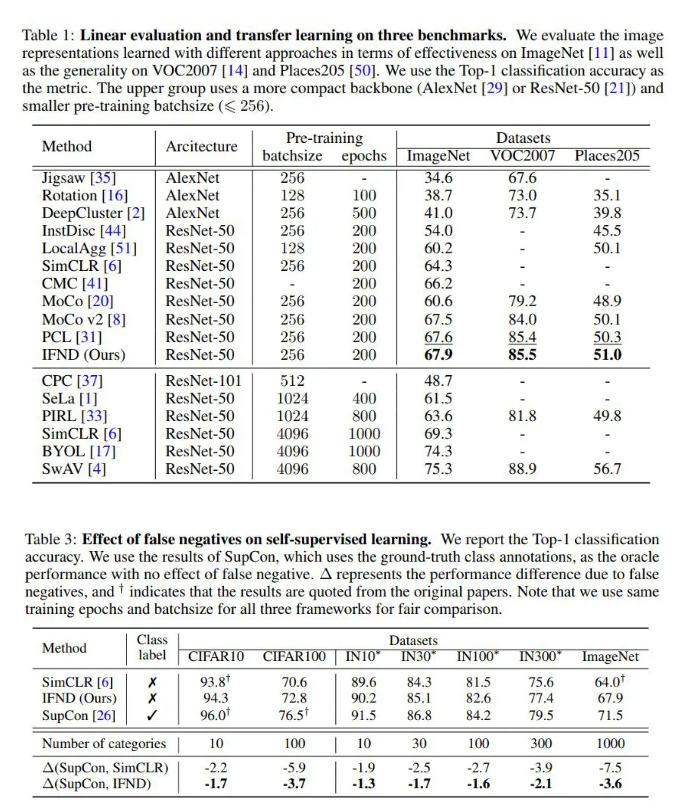
除此之外，作者还进行了不同删除策略的效果对比，进一步说明作者所提出的方法的有效性。

这个工作最吸引人的地方在于作者不再是通过一次聚类直接找到伪标签，然后进行假负样本的删除，而是设计了一个置信度计算方法，通过置信度逐步合理的删除假负样本，保证假负样本删除的正确性。同时作者巧妙的将置信度计算和模型的性能结合起来，有点课程学习的感觉。还是很有意思的。

负样本质量分析（are all negative equal）[4]

在之前的工作中，都是集中于选择更好的正样本或者更好的负样本，但是否简单的负样本就没有用？负样本的难度是否越难越好？为了回答这个问题，Facebook进行了关于负样本质量分析的工作，对整个对比学习中的样本选择工作进行了总结，同时也给了我们一些未来研究的启发。
4.1 亮点
本文针对负样本的质量对整个模型的影响进行了定量分析。

4.2 方法

由于这是一个定量分析的工作，本文作者并没有提出具体的方法，而是直接以 Moco v2 为基准模型，然后分析在不同难度的条件下模型的表现，最后总结出相关的结论。

作者首先定义了负样本难度的计算方式：锚点样本和负样本在隐式对比空间中的表征向量的点积。在此基础上，作者对负样本进行排序，然后在相同条件下进行 Moco v2 的训练。并通过删除模型中特定难度范围的样本来分析这些样本对整个模型性能的影响。最后作者发现了一些有意思的结论。首先，作者将整个结果总结成了一个图：

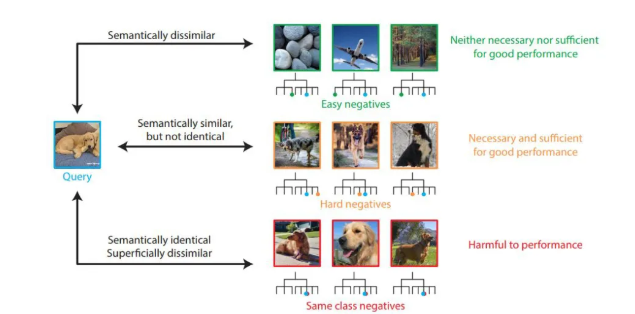
从图中可以得到以下结论：

  1. 最简单的 95% 的负样本是不必须的，对整个模型的影响非常小。最难的5%的负样本对整个模型的影响是巨大的，因此这些样本是必须的，而且这样的负样本数量也是足够的。仅在这些样本上进行训练就能够提升非常高。

  2. 最难的 0.1% 的负样本是不必要的，有时候甚至会对模型造成损害
  3. 通过对负样本的分析，难的负样本在类别上和锚点样本之间更相似（和简单样本相比），因此，在抽象语义上拥有更多的相似度对模型的影响更大一些。

作者还展示了一些具体的实验结果，如下图：

同时，作者也在未来工作中指出通过课程学习，逐步增加负样本的难度，有助于更好的对比学习。当然，本文的基础是基于图像分类的，也就是说所得到的负样本和正样本的质量是有保证的。那在更难的自然语言处理中，会不会有更有意思的发现呢？这个也是一个值得研究的地方。

 

总结

本文对对比学习中的采样策略进行了进一步的介绍，不再是如何选择更难的样本。而是考虑更全面的内容，如何解决 NLP 中的增强数据质量问题，如何提升对比学习的效率，如何在合适的时机选择恰当难度的样本提升对比学习的性能以及针对样本难度对模型性能整体定量分析。

从这些工作中可以看出，在对比学习中更好的采样不仅仅是指采集到更高质量的样本，同时还可以考虑在什么地方使用，在什么时候使用，以及如何使用。最后一个工作也指出了既然需要考虑样本难度，那么是否能将对比学习和课程学习有机结合起来，以更合理的方式实现对采集样本的利用，进一步提升模型的性能。这些都是非常有意思，有价值的研究方向。

参考文献

[1] Yan Y, Li R, Wang S, et al. ConSERT: A Contrastive Framework for Self-Supervised Sentence Representation Transfer[J]. arXiv preprint arXiv:2105.11741, 2021. 

[2] Wang G, Wang K, Wang G, et al. Towards Solving Inefficiency of Self-supervised Representation Learning[J]. arXiv preprint arXiv:2104.08760, 2021. 

[3] Chen T S, Hung W C, Tseng H Y, et al. Incremental False Negative Detection for Contrastive Learning[J]. arXiv preprint arXiv:2106.03719, 2021.. 

[4] Cai T T, Frankle J, Schwab D J, et al. Are all negatives created equal in contrastive instance discrimination?[J]. arXiv preprint arXiv:2010.06682, 2020.

·