OpenAI 在博客中介绍其最新研究解决Math Word Problems，并发表相关文章《Training Verifiers to Solve Math Word Problems》。文中训练了一个系统，它解决小学数学问题的精确度几乎是经过微调的GPT-3模型的两倍。它解决的问题大约是真实孩子的90%:一小部分9-12岁的孩子在我们数据集的测试中得分为60%，而本文的系统在同样的问题上得分为55%。这一点很重要，因为现在的人工智能在常识性的多步骤推理方面仍然很薄弱，即使是小学生也很容易做到。作者通过训练他们的模型来识别其自身的错误最终获得这些结果，这样它就可以反复尝试，直到找到一个可行的解决方案。

论文链接：https://arxiv.org/abs/2110.14168

数据集：https://github.com/openai/grade-school-math

引言

像GPT-3这样的大型语言模型有许多令人印象深刻的技能，包括它们模仿多种写作风格的能力，以及它们广泛的事实知识。然而，他们很难完成需要精确的多步骤推理的任务，比如解决小学数学应用题。尽管该模型可以模拟正确解决方案的节奏，但它经常在逻辑上产生严重错误。

为了匹配人类在复杂逻辑领域中的表现，我们的模型必须学会识别它们的错误，并仔细选择它们的步骤。为此，我们训练verifiers来评估所提出的解决方案是否正确。为了解决一个新问题，我们使用验证器从许多提出的解决方案中选择最好的。我们收集了新的GSM8K数据集来评估我们的方法，该数据集已经发布来促进研究。

在博客中通过10个例子展示了由我们的新方法、验证和基线方法、微调生成的解决方案。

GSM8K数据集

GSM8K由8.5K高质量的小学数学应用题组成。每个问题都需要2到8个步骤来解决，解决方案主要包括使用基本算术运算(+ − × ÷)进行一系列的基本计算，以得到最终答案。经过微调的最先进的语言模型在这个数据集上表现很差，这主要是由于问题的高度多样性。同时，GSM8K解决方案只依赖于基本的概念，因此实现高测试性能是一个容易实现的目标。

GSM8K中的解决方案被写为自然语言而不是纯粹的数学表达式。通过坚持自然语言，人类更容易解释模型产生的解决方案，我们的方法仍然是较为不可知的。

训练verifiers:从错误中学习的模型

数学推理的一个重大挑战是对单个错误的高度敏感性。自回归模型一个令牌一个令牌地生成每个解决方案，它没有纠正自己错误的机制。快速偏离的解决方案将变得不可恢复，这可以从所提供的示例中看到。

我们通过训练verifiers来评估模型生成的解决方案的正确性来解决这个问题。verifiers会得到许多可能的解决方案，这些解决方案都是由模型本身编写的，并且它们被训练以判断哪些方案是正确的。

为了在测试时解决一个新问题，我们生成100个候选解决方案，然后选择verifiers排名最高的解决方案。verifiers受益于这种固有的可选性，以及验证通常比生成更简单的任务这一事实。

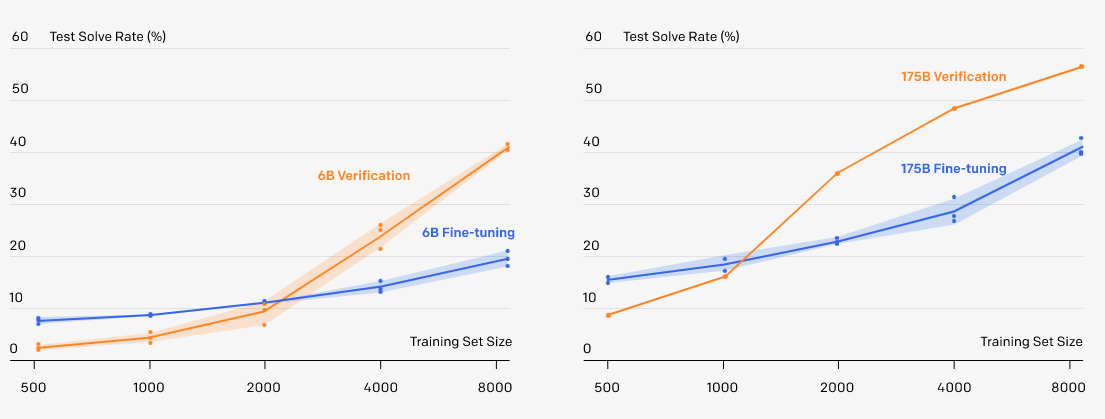
我们发现，只要数据集足够大，验证就能极大地提高性能。在数据集太小的情况下，我们认为验证者通过记忆训练集中的最终答案而过拟合，而不是学习任何更有用的数学推理属性。

在完整的训练集上，6B参数验证的性能略优于经过微调的175B参数模型，提供了大约相当于模型大小增加30倍的性能提升。此外，如果我们根据目前的结果进行外推，那么使用额外的数据进行验证似乎更有效。

结论

产生正确的论据并识别错误的论据是开发更普遍的人工智能的关键挑战。小学数学是测试这些能力的理想平台。GSM8K中的问题在概念上很简单，但一个细微的错误就足以破坏整个解决方案。识别和避免这些错误是我们模型发展的关键技能。通过训练verifiers，我们教我们的模型区分好的解决方案和不太可行的解决方案。当我们试图将我们的模型应用到逻辑上更复杂的领域时，我们期望这些技能变得越来越相关。

内容中包含的图片若涉及版权问题，请及时与我们联系删除