把神经网络的限制视为无限多个残差层的组合,这种观点提供了一种将其输出隐式定义为常微分方程 ODE 的解的方法。连续深度参数化将模型的规范与其计算分离。虽然范式的复杂性增加了,但这种方法有几个好处:(1)通过指定自适应计算的容错,可以以细粒度的方式用计算成本换取精度;(2)通过及时运行动态 backward 来重建反向传播所需中间状态的激活函数,可以使训练的内存成本显著降低。
另一方面,对神经网络的贝叶斯处理改动了典型的训练 pipeline,不再执行点估计,而是推断参数的分布。虽然这种方法增加了复杂性,但它会自动考虑模型的不确定性——可以通过模型平均来对抗过拟合和改进模型校准,尤其是对于分布外数据。
近日,来自多伦多大学和斯坦福大学的一项研究表明贝叶斯连续深度神经网络的替代构造具有一些额外的好处,开发了一种在连续深度贝叶斯神经网络中进行近似推理的实用方法。该论文的一作是多伦多大学 Vector Institute 的本科学生 Winnie Xu,二作是 NeurIPS 2018 最佳论文的一作陈天琦,他们的导师 David Duvenaud 也是论文作者之一。

具体来说,该研究考虑了无限深度贝叶斯神经网络每层分别具有未知权重的限制,提出一类称为 SDE-BNN(SDE- Bayesian neural network )的模型。该研究表明,使用 Li 等人(2020)描述的基于可扩展梯度的变分推理方案可以有效地进行近似推理。
在这种方法中,输出层的状态由黑盒自适应随机微分方程(SDE 求解器计算,并训练模型以最大化变分下界。下图将这种神经 SDE 参数化与标准神经 ODE 方法进行了对比。这种方法保持了训练贝叶斯神经 ODE 的自适应计算和恒定内存成本。
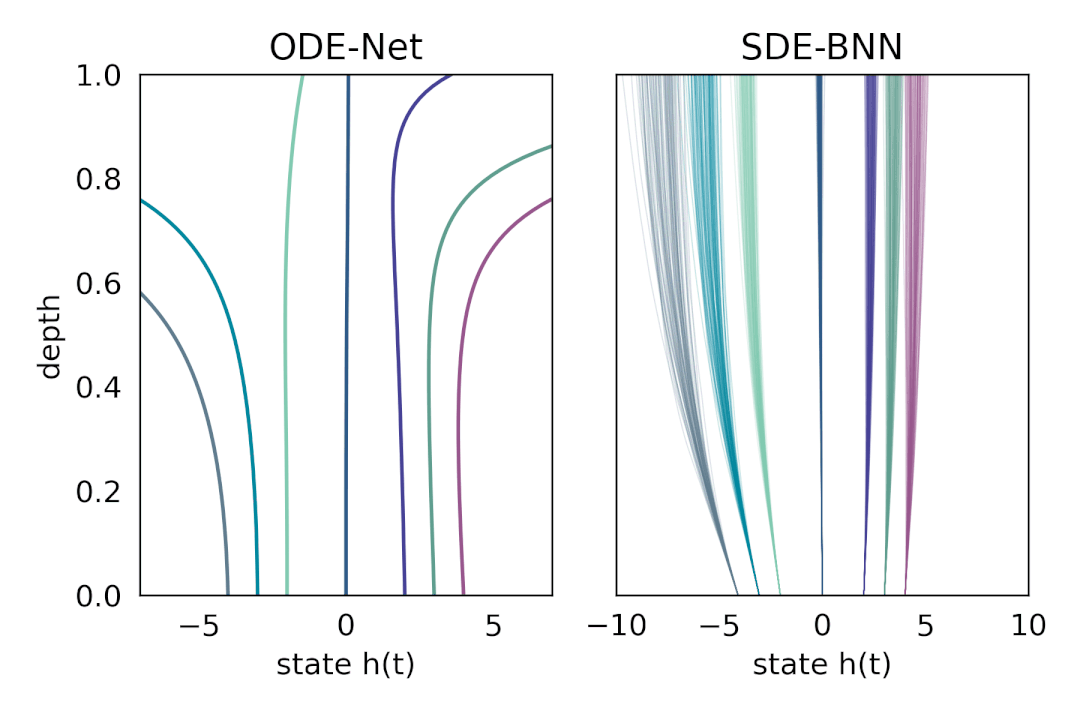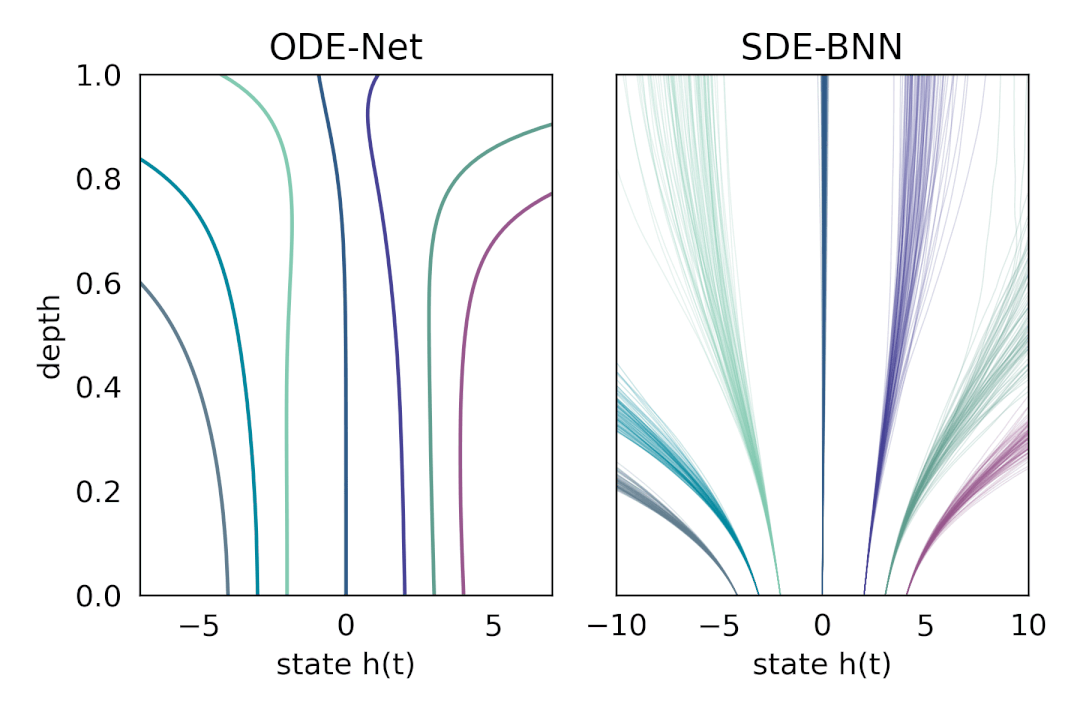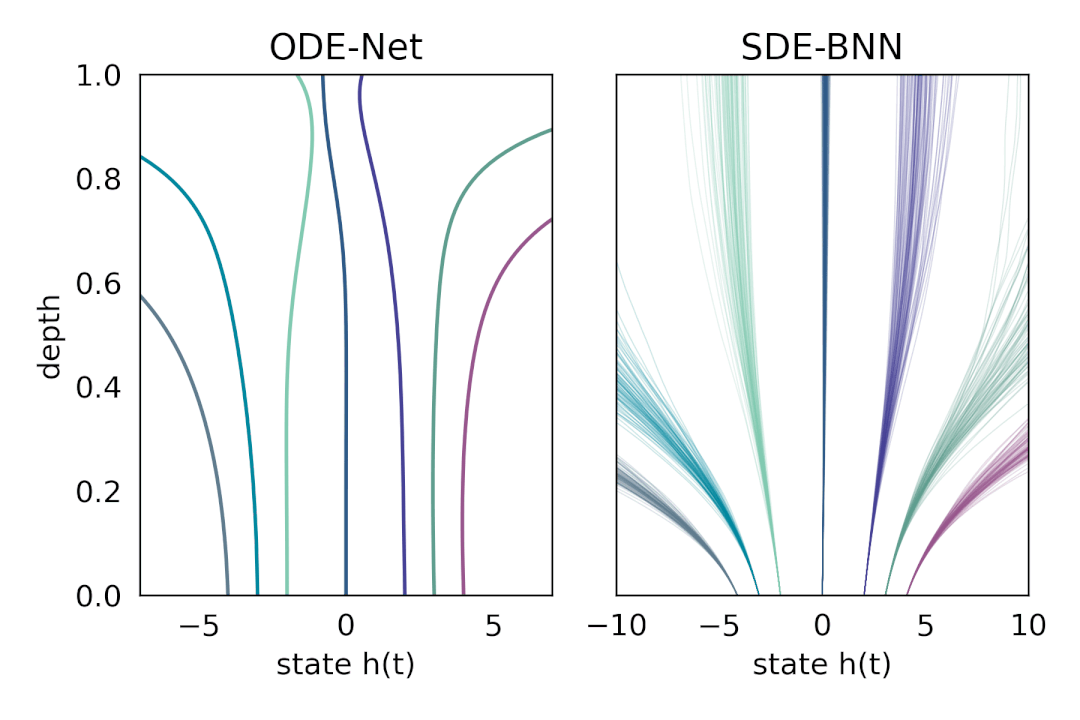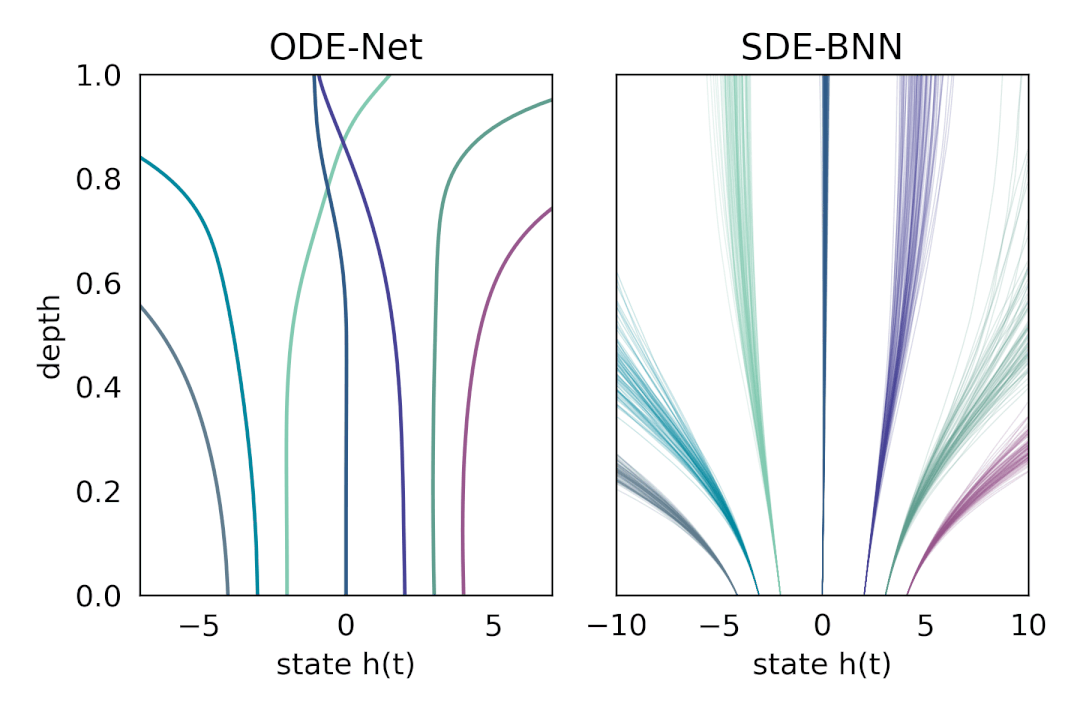
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢