1 前言
图神经网络(Graph Neural Networks, GNN)在诸多图任务上的巨大潜力已经有目共睹。众多学者也从不同的视角开始对GNN背后的机制开展探索,诸如[1]指出了GNN的低通滤波特性,[2]证明了GNN等价于1-WL test,[3]揭示了统一优化目标下的GNN传播机制。其中GNN的低通滤波特性引起了业界广泛关注,因为这意味着GNN可以有效过滤数据中的噪声,平滑邻居节点的表示,达到邻近节点具有相似表征的目的。故而,这使得GNN非常适用于同配图(Assortative Graph / Homophily Graph),即网络中有相同标签的节点倾向于互相连接。以广泛使用的三个数据集,Cora, citeseer和pubmed为例,这三个数据集都属于学术网络,其特点是网络有极强的同配性。由于GCN的消息传递方式是利用均值聚合所有邻居的信息,所以可以很好地学习到学术网络的归纳偏置(Inductive bias)。
但是,我们不禁要问,现实世界中的网络是否都具有同配性这一特点呢?其实早在2003年,密歇根大学的物理学教授Mark Newman就已经在论文《Mixing patterns in networks》[4]中对现实世界里的各种网络的同配性做了分析,如下图所示:
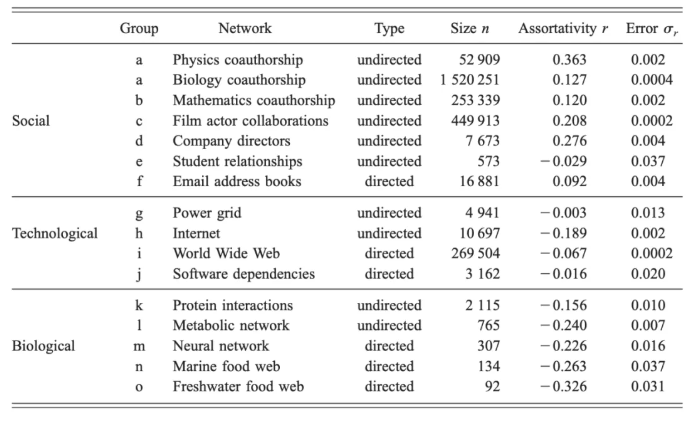
对于指标Assortativity (r),其值越大,代表同配性越强,反之则异配性(Disassortativity / Heterophily)越强。从图中我们可以看到一个不争的事实,学术网络的同配性是各种网络中最强的,但是很多网络并不具有同配性,反而有很强的异配性。所以GNN在学术网络上的优越性能难以佐证其在真实世界应用的良好泛化性。论文[5]的实验中显示,在异配性强的网络中,GCN、GAT等在学术网络中表现好的方法的性能,还不如不利用图结构信息的多层感知机。我们需要认真审视这一现象,怎样才能解决图神经网络在异配图上效果不佳的问题?
2 如何解决异配图节点分类问题
目前,已经有很多工作尝试将图神经网络泛化到异配图上,我们以较早开始对这一问题开展探索的三篇代表性论文出发,从三个不同的角度,来说明如何让图神经网络在异配图上也能取得很好的效果。
1.图结构学习
解决异配图问题最直接的一个方法就是,通过改变图结构,使得原本的异配图变为同配图,这样在同配图上表现好的方法就可以继续用在异配图中。论文[6]中提出了一种利用利用结构信息为节点选择邻居的模型:Geom-GCN。其基本思想是,具有相似结构信息的节点(例如桥节点、中心节点等)可能属于同一个类别,因此可以利用结构信息来为节点选择新的邻居,增加图的同配性。其模型流程如下图所示:
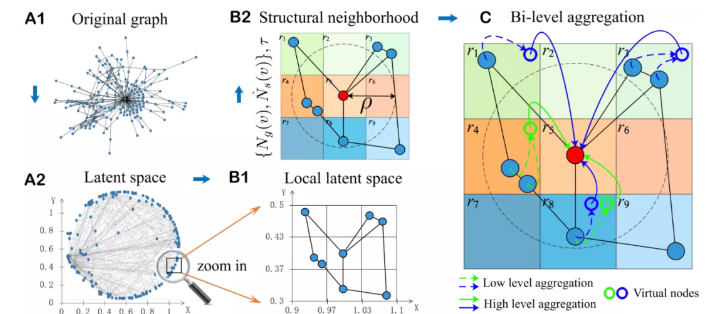
首先,Geom-GCN利用传统的网络嵌入方法学习到每个节点的低维向量表示;然后选择向量相似的节点作为新的邻居,显示地捕获了节点之间的结构相似性,增加了图结构的同配性;然后再将原始邻居和新邻居的信息进行聚合,更新节点的表示。类似的思想其实[7]也做了初步尝试,除了原始的图结构以外,他们基于节点特征显式地构造了一个新的特征图,这样假如原始图结构不具备同配性特点的时候,新的基于节点特征的特征图或可以起到效果。进一步地,也可以直接抛弃掉显式构造特征图的步骤,直接学习出一个新的图结构[8],
2.图表征分离
除了图结构学习外,还有一些方法尝试通过改进图神经网络的消息传递机制来提升其表达能力。H2GNN[9]从理论上证明了分离节点自身的表征和邻居聚合的表征可以将图神经网络泛化到异配图上。然后它设计了三个关键的消息传递机制,通过适当集成,可以帮助图神经网络提升在异配图上的性能。
-
自身表征和邻居表征分离。H2GNN认为图神经网络通过层层堆叠的方式聚合邻居信息,会使得节点的表示变得相似,导致模型不能很好地区分不同类别的节点,因此它的第一个设计是分离自身表征和邻居表征:,其中代表拼接操作,是层数,是聚合函数,是节点的邻居集合。 -
引入高阶邻居信息。除了分离表征以外,H2GNN还证明了高阶邻居对于异配图的节点分类是有帮助的,通过引入高阶邻居,模型可以学习到异配性主导(heterophily-dominant)的信息,其消息传递机制为: ,其中 代表了距离中心节点距离为的邻居。 -
中间层表征融合。在做完每一层的信息聚合后,H2GNN将所有中间层的表征拼接在一起,来捕获图中的局部和全局信息,这种设计更准确地模拟了异配图中邻居表示的分布:,其中是消息传递的总层数。
H2GNN通过以上三个设计的集成,缓解了图神经网络随着层数的增加难以区分不同类型的节点的问题,提升了图神经网络的表达能力。
3.图信号处理
在自然界中,信息以不同的频率进行传输,其中较高的频率通常用来编码细节信息,而较低的频率则代表了全局结构。那么同配图和异配图是否具有不同频率的信息呢?论文[5]设计了一个从图信号处理角度来分析同配图和异配图的实验,如下图所示:
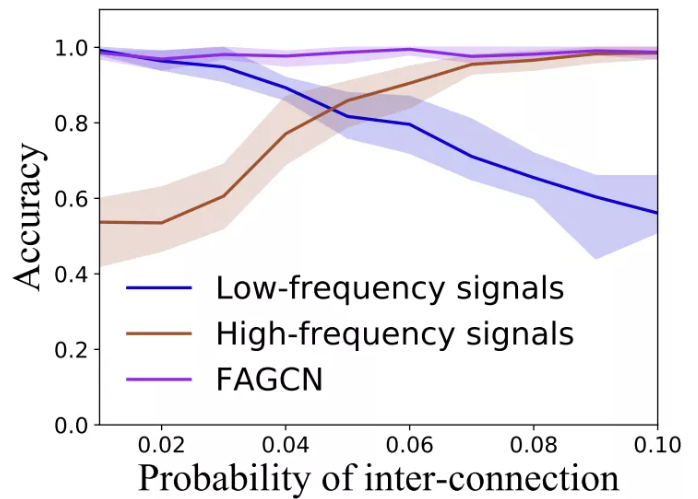
它利用随机块(Stochastic Blockmodel,SBM)模型生成了一系列图数据集,其中类内连接概率固定为0.05,而类间连接概率从0.01逐渐增大到0.1,随着类间连接概率的增大,图结构逐渐显现出异配性。同时它将输入特征分为低频特征和高频特征,然后在生成数据集上进行性能测试。从图中我们可以发现,低频特征在同配图上表现较好,而高频特征在异配图上表现较好。结合论文[1]中提到的GCN是一个低通滤波器,我们不难明白为什么大多数图神经网络都不能再异配图上取得很好的效果,因为对于异配图分类重要的高频特征已经被过滤掉了!
所以,如果想让图神经网络能够在同配图和异配图上都有很好的表现,我们就需要模型能够同时具有低通滤波和高通滤波的能力。为了达到这一目的,论文[5]提出了频率自适应图神经网络(Frequency Adaptation Graph Convolutional Networks,FAGCN)。它首先设计了一个低通滤波器和一个高通滤波器,其频率响应滤波函数如下:
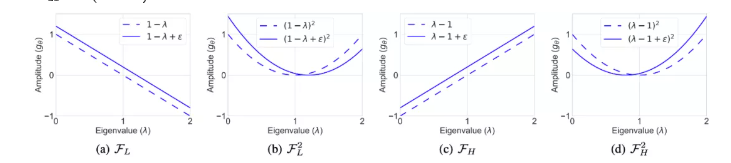
通过这两个滤波器,模型可以分别提取到模型的低频和高频特征,然后通过注意力机制进行信号融合:,其中为特征矩阵,为节点的特征。为了更好地解释信号融合背后的原理,我们可以对公式进行进一步的展开:。我们可以看到,其本质仍然是图神经网络的消息传递机制,对自身信息和邻居信息进行融合。在注意力机制中,注意力系数的和为1,即,所以的范围就限制在之间。这与传统的基于注意力的图神经网络(比如GAT)略有不同,FAGCN并不限制注意力系数一定为非负数,这一点是解决异配图的核心关键。
但是该消息传递函数仍然存在很多不足,最大的问题是,在节点聚合邻居消息时,其注意力系数对于每个邻居是相同的(在很多论文中被称为各向同性),这样会极大程度地限制FAGCN的表达能力。所以,我们对该消息传递机制进行一些细微的修改,其消息传递函数变为,即每一个邻居都有其独有的系数,达到了各向异性的目的,增强了模型的表达能力。对于系数的学习,FAGCN采用和GAT一样设计,所不同的是,为了保证系数的范围限制在之间,FAGCN利用tanh激活函数代替了GAT中的softmax,即。可以看到,FAGCN中关键步骤即学到一个可以区分正负的权重系数,这一步骤具有谱域滤波的理论基础,自适应能力强,同时操作非常简洁,因为普遍意义上看,tanh的激活函数可以即插即用到任何其他的图神经网络之中,使得其他图神经网络也具备这种区分能力。
最后FAGCN还提供了理论证明:低通滤波可以让节点表征变得相似,而高通滤波会让节点表征变得不同。通过正系数聚合邻居可以模拟低通滤波,通过负系数聚合邻居可以模拟高通滤波。所以FAGCN可以在同配图和异配图上都取得很好的效果。
3 思考与总结
以上三个思路从不同角度都对GNN如何泛化到异配图上开展研究,但可以看到,本质上还是会落脚到图结构本身来。他们或者是探索图结构本身不同阶数节点的不同影响,或者是直接修改图结构,比如学习图结构或者使得图结构上具有正负判别性。近段时间来,对于异配图上的GNN的探索吸引了众多的注意力。与此同时,也有学者关注到GNN并非在所有异配图上都不适用。这一点,笔者也表示同意,可以试想这样一张异配图,具有A标签节点的邻居都是B,而具有B标签节点的邻居都是A,以GNN的信息传播机制来讲,A和B只是互换了一下信息而已,而A标签节点,他们之间的表征还依然是相似的,也就是说对于A的分类,应该也依然会奏效。B节点同理。因此,如何更准确界定GNN的适用范围,或者真正实现普适性,还需要进一步思考。
[1] Simplifying Graph Convolutional Networks. ICML 2019.
[2] How Powerful are Graph Neural Networks? ICLR 2019.
[3] Interpreting and Unifying Graph Neural Networks with An Optimization Framework. WWW 2021.
[4] Mixing patterns in networks. Physical review E, 2003
[5] Beyond Low-frequency Information in Graph Convolutional Networks. AAAI 2021.
[6] Geom-gcn: Geometric graph convolutional networks. ICLR 2020.
[7] AM-GCN: Adaptive Multi-channel Graph Convolutional Networks. KDD 2020.
[8] Graph Structure Estimation Neural Networks. WWW 2021.
[9] Beyond Homophily in Graph Neural Networks: Current Limitations and Effective Designs. NeurIPS 2021.
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢