现实生活中，许多情况下由于负类样本的获取比较困难或负类样本太过多样，因此模型训练时只有正样本和大量的未标注样本。为处理这种情况，PU学习（Positive and Unlabeled Learning，简称PU learning）被提出，以处理只有正类和未标注数据情况下的分类器训练问题。本文研究了实例相关的PU分类，具体是指其中一个正样本是否会被标注（由 \( s \) 表示）不仅与类别标签  \( y \) 相关，还取决于特征向量 \( x \) 。换而言之，正样本被标注的概率并不满足以前工作的假设——即所有正样本以相同概率被均匀标注。因此，本文提出了标注偏差估计的方法来处理这种实例相关的PU学习问题。目前，该文已发表于人工智能国际顶级期刊《IEEE Transactions on Pattern Analysis and Machine Intelligence》。

文章链接：https://ieeexplore.ieee.org/abstract/document/9361303

本文中的PU学习方法与现有的方法比较。(a)为现有的实例无关PU学习方法，(b)为本文中的实例相关PU学习方法。

本文通过建模分析提出了一种名为“标注偏差估计”（LBE）的概率方法。它估计了正类数据的标注偏差并训练分类器。通过该方法模型的构建过程和对实验结果的分析，可以得到LBE的优势包括四个方面：

1)一般性：该模型框架的一般性包括两个方面，一是LBE可以广泛地适应当下的主流分类器，如本文提出的LF和MLP；另一方面，只要改变用户定义的  ，LBE就可以灵活地描述各种标注偏差。

2)最优性：LBE可以利用具有明确目标函数的Logistic回归来实现，并且可以从理论上证明其解的存在性和局部唯一性。

3)泛化性：可以从理论上证明，对于LBE模型如果正类数据和未标注数据的数量足够大，期望风险将收敛于经验风险，即该模型在未知数据上具有良好的泛化性。

4)实用性：LBE模型与许多现有的PU分类器不同，其不需要预先估计先验概率  ，并且该先验概率实际上不容易获得。此外，LBE模型不包含任何超参数。因此，它可以在各种实际场景下轻松实现。

在LBE方法中，明确建立了输入特征向量 \( x \epsilon R^d \) 、真实标签值 \( y \epsilon \{0, 1\} \) 和变量 \( s \epsilon \{0,1\} \) （研究背景中已作定义，表示  \( x \) 是否被标注）之间的关系（见图1(b)）。 \( x \) 、\( y \)  和 \( s \) 之间的关系可以用图1(b)所示的图模型来描述。首先，数据的标签值  \( y \)（即该数据所属的类别）显然取决于数据的特征向量 \( x \) 。其次，该数据的 \( s \) 值（即该数据是否会被标注）不仅取决于标签值 \( y \) ，还取决于其特征向量 \( x \) 。这也是LBE方法与现有的PU学习方法最大的不同之处，LBE方法在考虑了依赖关系 \( y\rightarrow s \) 之外还考虑了关系 \( x\rightarrow s \) 。在实际问题中，由于数据的标注难度或标注者的专业特长等各种因素，因此考虑标注偏差，即考虑  \( x\rightarrow s \)  是十分必要的。

基于上述定义，并结合图1(b)，可以得到以下关于、和的产生式，即

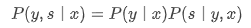
对于输入特征向量 \( x \) 的后验概率 \( P ( x|y) \)，可等效为参数为 \( \theta_{1} \) 的score函数 \( h(x; \theta_{1}) \) 。对于 \( P (s| y, x) \)，由于只有正类数据才有可能被标注，因此可得以下各式：

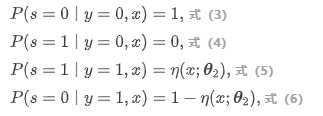其中 \( \eta(x; \theta_{2} ) \) 是参数为 \( \theta_{2} \) 的score函数，其值表示在 \( y=1 \) 时  \( x \) 被标注的概率。

本文提供了 \( h(x; \theta_{1}) \) 和  \( \eta(x; \theta_{2} ) \) 的两种实现方式。第一种基于Logistic函数（结合本文方法命名为“LBE-LF”），第二种是基于典型的多层感知器（MLP）神经网络，该模型在本文中称为“LBE-MLP”。

 

 

 

内容中包含的图片若涉及版权问题，请及时与我们联系删除