可解释性(Interpretability or Explainability)
什么是可解释性(what)
在机器学习领域,可解释性是指对一个算法的原理或者得出结果的依据做出解释。如在17年发布的可解释性研究领域的指南里面讲到:
Interpretation is the process of giving explanations to humans.
也即可解释性是用人类的语言来解释算法过程,可解释性有两个概念Interpretability和Explainability,前者主要指的是对于传统的统计学习算法(如决策树、支持向量机等)的判决机理给予解释,这样的算法的推导过程都是有迹可循的被称为白盒模型。后者主要指的是对于复杂的难以管中窥豹的算法(如神经网络)进行判决归因,这样的算法基本上都是由大量的非线性函数堆栈而成,难以直观地剖析内部机制而被称为黑盒模型。(后面提到的内容是针对于后者来展开的)
不同的人群对于了解一个事件的缘由是有不同等级的,比如了解生活中的一道菜为什么很美味,普通食客可能只是了解到这是用什么主要材料和烹饪手法做的(甚至可以是因为这道菜是某某品牌的),而对于厨师他们会去细究调味品和烹饪工艺及时长对其的影响,所以对于不同的人,对模型的可解释性的深度是有巨大差异的。
为什么需要可解释性(why)
黑盒模型不仅是内部不可知的,也是拿来主义开箱即用的,但是对于参与系统构建及应用过程中的人来说,可解释性是有不一样的价值并且必不可少。
- 算法工程师:在算法构建的过程中,工程师需要根据实际的应用场景选择不同的框架和网络结构来获得更高的精度和泛化能力,那么他们需要进入网络的内部结构,研究不同的成分的功能并且对整体效用的影响。这时候的可解释性针对于网络结构效用,用于提高网络性能。
- 产品使用者或受用者:算法构建出来后,需要被接纳被使用,那么黑盒模型中的不可见性便是可能存在的风险,针对一些决策失误风险较高的领域如医疗、金融,构建一个诊断和投资决策的推荐系统,可解释的决策机理是使用者更加关注的点,他们期望知道得出决策是依据什么信息经过怎样的逻辑推导,以保障他们采用其的信心。
- 领域专家:传统的领域专家需要了解某个领域的知识后,针对不同的应用需要去构建有效决策依赖的特征和相应的规则,当模型具有可解释性后,他们可以通过研究高效模型获取其依赖的特征和规则,这往往是启发性的知识,并可以启发该领域后期的研究。
现有的可解释性算法问题和公理设定
目前针对深度神经网络的可解释性算法有Gradients和Back-propagation based approaches 两大类,但是当归因结果与人类经验相异的时候我们很难去判断出到底是确实是算法模型的问题还是归因技术本身的问题,因此需要设定可解释性算法必要满足的公理,由此用满足公理的技术进行归因得到的结果必定是模型所应有的。在积分梯度算法的论文(Axiomatic Attribution for Deep Networks)中提出了敏感度(Sensitivity)和实现不变性(Implementation Invariance)两个公理。下面分别阐述这两个公理和现有的可解释性算法在这两个公理上的表现。
基线值:当我们把一件事情的发生归结于某个原因的时候,我们就可以把没有该原因的情况当做基线值,如状态不佳的原因是失眠(有状态),那没有失眠就是基线值,因为没有失眠对应的输出是啥事没有(无状态)。对于一个图像识别系统来说,基线值可以是一张全黑的图片;而对于一个NLP系统而言,基线值可以是全部值为0的词向量。
1、敏感度(Sensitivity)
如果针对一个特征,当输入非基线值的时候应当获得有状态的预测(基线值对应无状态);当选取两个不同的输入值(相对于基线值而言)时,模型应该输出不同的预测,这样子该特征将被赋予非零归因,简而言之就是梯度处处不为零。(个人感觉原论文中斜体部分不是很有必要,毕竟把基线值当成零输入充当两个输入值其一,那么后面的情况可以涵盖前面的情况)。
2、实现不变性(Implementation Invariance)
尽管内部实现不一致,但对于所有的输入,输出结果都是一致的两个模型被称为功能等效。面对两个功能等效的模型进行归因分析而获得相同的成因的归因算法满足实现不变性,这样子便是将得到输出的责任仅仅是归结于输入,与算法内部实现路径脱敏。
梯度归因(Gradients)和基于反向传播的归因(Back-propagation based approaches )
1、梯度归因(Gradients)
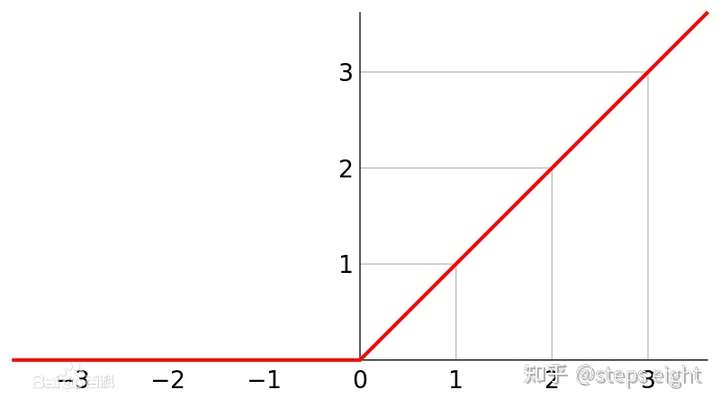
对于深度网络而言,输出对输入的直接梯度是对模型参数的自然模拟,然而深度网络其本身就是一个非线性的函数表达,可视为多个非线性函数的堆栈体。非线性函数不可避免地存在梯度饱和的阶段,在该阶段内梯度趋向于零而违背了敏感性准则。ReLU函数是一个极度简单的非线性函数,下面以此构建一个具体的非线性系统函数进行讨论。
以 为基线,当
的时候可以得到不同的结果。即
,但是
不满足梯度处处存在的条件(
均是),即违背了敏感性。
对于实现不变性来说,由于假定的非线性函数处处可微,设 为输入,
为模型内部实现细节,由链式法则可以得知
即基于输入输出的直接梯度是可以忽略模型内部实现细节的,故满足实现不变性。
2、基于反向传播的归因
基于反向传播的归因技术中,有DeepLift和Layer-wise relevance propagation (LRP)这两种技术通过设置跨度较大的离散值来保障梯度处处存在,所以满足了敏感性原则,但是由于离散函数不满足链式法则即
故函数内部的实现细节不可忽略,所以不满足实现不变性。
积分梯度算法(Integrated Gradients)
积分梯度算法的结合了直接梯度和基于反向传播的归因技术DeepLift和LRP的分而治之的设计思想,满足敏感性和实现不变性的公理。设输入为 ,基线值为
,函数映射表示为F,对输入的第
个维度求积分梯度可以表示如下:
从上式的表达可以看出积分梯度算法仅仅考虑了模型的输入输出且函数处处可微,不需要模型内部细节的参与,因此积分梯度算法是满足实现不变性的。而对于敏感型的公理,文章直接提出了一个新的公理为完整度(Completeness),并且直白地说完整度是敏感型的更高实现,其本身蕴含着敏感性,并没有进行具体的讲述和论证,下面尝试着按照我的理解解释一下。
完整度(Completeness)
归因技术以积分的方式加和了从基线值到输入间的输出值称为满足完整度。直接梯度是选取当前输入一个点进行输入输出的归因,当输入的特征值刚刚好处于梯度饱和阶段时,获得的归因结果在该特征上的归因比重往往微乎其微,但该输入特征并非不重要,这其实才是敏感性真正要解决的问题。而积分梯度通过在基线值和输入值之间选取了无限多个积分点进行积分加和即满足完整度,这时并不拘泥于梯度饱和阶段而更像是对 整体进行均衡加权归因,这样便巧妙地解决了梯度饱和问题,因此说完整度是蕴含了敏感性,是其更高的实现。
积分路径的选择
在公式4中标准化了积分梯度算法,而其中用 来表示从基线值到输入值间的积分过程中当前选取的归因对象的幅值比例,而
的变化规律对应着不同的积分路径,比如当
是一个常数的时候,积分过程中的积分对象则是沿着直线进行线性插值得来的即积分路径是直线,而当
是一个随积分步骤而变化的变量时,获得的积分路径可以是多样的如图2。
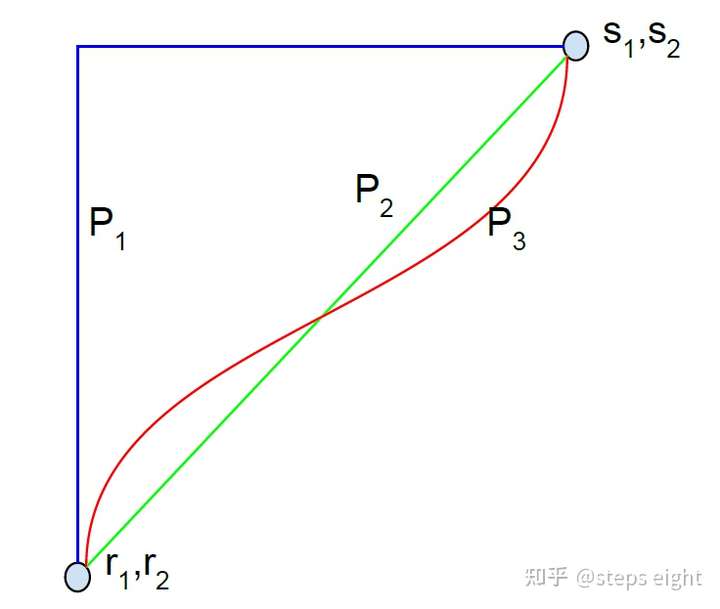
为了将这个积分路径的部分也表达进公式,定义了一个路径函数 ,定义如下:
由此可以将原先的积分梯度算法的表达式修改为:
当积分路径是直线的时候, 显然是一个常量,而且直线插值也是积分梯度算法最典型的积分路径,因为它满足对称性保留(Symmetry-Preserving)。
保对称性(Symmetry-Preserving)
保对称是指交换函数中的两个参数位置进行计算并不会改变函数的输出值,即 ,这样的函数称为满足保对称性,而这两个参数是对称的(symmetric),比如一个函数定义为:
显而易见,输入向量中的每一个维度 在该函数下都是相互对称的。
保对称性保障了归因技术对数据输入格式的低限定性,多个特征不需要按照既定的模式输入归因系统,不按顺序直接输入也能正确归因,因此大大降低了开展归因前的预处理需要。比如在目标检测的图像识别系统中,进行归因时并不需要对图像像素点的位置和整体排布结构进行设定,只需要直接输入都可以进行归因。
两大公理的形象化理解
虽然这篇文章的概念和公式并不是非常难以理解,但是为了更好的理解可解释性的公理设定潜在的意义,下面根据李宏毅老师的视频和我的理解尝试着作形象化解读。
敏感性
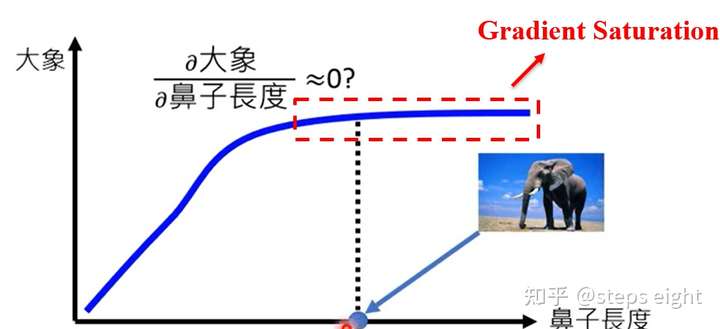
敏感性准则要求归因技术在模型函数上梯度处处存在,本质上由于模型函数往往是一个非线性函数不可避免的存在梯度饱和的区域,当处于梯度饱和阶段时有效特征往往被无效归因,为此才要求梯度处处存在。比如在一个动物分类系统中,模型对大象进行学习时可能会以大象的鼻子作为判别依据(因为大象相对于其他种类的动物,鼻子格外的长),对一张大象图像进行识别的时候,在图像中大象的鼻子在初期相较于大象身高比值为0.2的时候,系统对该类别的置信度随着比值的增长逐渐提高(梯度存在),但鼻子到达足够长的时候(可能是0.5比例)系统对大象类别的置信度随比值增长而不再显著提高甚至停滞(梯度饱和),此时利用直接梯度的归因技术得到的结果在鼻子这个特征上将是不显著的,但是我们知道事实并非如此。因此,敏感性公理就是要求归因技术在面对梯度饱和的时候能够在辨识性特征上保留有效梯度,以致于合理归因。
实现不变性
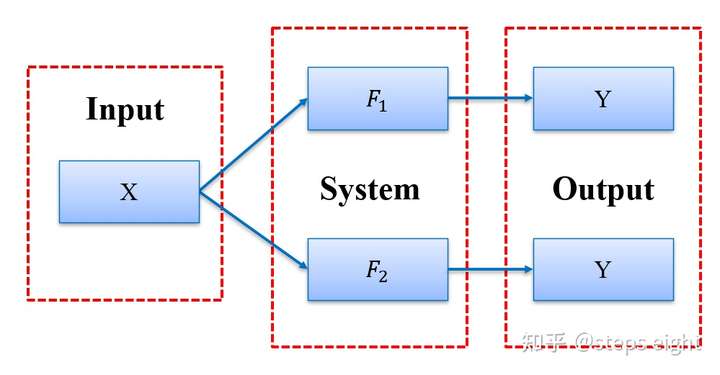
当 和
的内部实现不一致但满足
时,称为这两个函数是功能等效的,此时若针对一个相同的输出值对这两个函数进行归因分析理应得到相同的归因结果,就称这个归因技术是满足实现不变性的。
积分梯度的应用变式及应用实例
基准的选择
应用积分梯度的关键点是选择一个好的基准值,这样的基准值需要满足接近零值的输出分数,即这样的基线值可以不包含任何信号,这样我们才能将归因结果仅归结于输入值。例如在目标识别网络中,一个全黑图(0值)意味着没有任何目标;但是其也不是仅有的合适的基准,一个由噪声合成的图像也能达到同样的效果。但是全黑图作为基准进行归因后,得到的归因结果在视觉上具有清晰的边缘。
应用变式
积分梯度可以通过加和的方式来逼近,这样可以在保障归因效果的基础上最大程度降低计算量。在实际应用中可以沿着基准值和输入值的路径上线性插入多个等间隔的值,在这些值上求得对输出分数的梯度然后进行均衡权值加和,设 为积分的黎曼和近似的步值,在实际测试中,当选取20到300步值足以在5%的偏差内近似积分,应用变式修改如下:
应用实例
在文章的工作中给出了5个应用实例,包括两个图像模型,两个自然语言模型,和一个化学模型,下面仅给出两个图像模型。
1、目标检测网络
论文中,作者构建了一个基于GoogleNet的目标检测网络针对ImageNet数据集进行学习,将全黑图(像素强度为0)作为基准输入,以输出预测类别中分数最高的类别进行归因,利用积分梯度算法来研究网络做出预测时哪些像素点提供了最重要的贡献。并且为了展现积分梯度算法的优越性,作者还对比了对输入输出做直接梯度的结果。如下图,积分梯度明显地更能突出输入图样的可辨识特征。

2、糖尿病性视网膜病变图像的预测
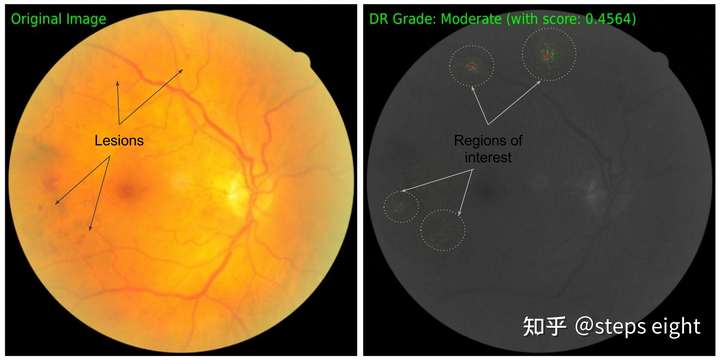
深度网络被提出用于预测视网膜眼底图像中糖尿病视网膜病变的严重级别,作者构建了一个对验证集有良好预测精度的网络,并利用积分梯度的归因算法来研究哪些特征对网络的决策是重要的,这对于视网膜专家而言是重要的,找出决策依赖的关键特征并与日常的诊断依据进行参照对比可以提高使用者对该模型的信任。可以同样的全黑图作为基准值,对RGB多个通道单独应用积分梯度算法进行加和,然后先将原图灰度化再将正值归因结果加在绿色通道上,将负值归因结果加在红色通道上。结果如下图,积分梯度算法定位到类似病变节点的像素点上,其中病变内部是负值归因而外部是正值归因。
参考文献:[1] Axiomatic Attribution for Deep Networks
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢