本文主要介绍图神经网络相关的内容，以从序列神经网络到图神经网络为切入点，逐步讲述从CNN到GCN，从GCN到GraphSage，从GCN到GAT三个方面进行论述。

一、从序列神经网络到图神经网络

当我们将一个NLP序列问题转换为一个图结构问题时，GNN图神经网络的工作就开始派上用场了。

不过，我们首先要弄清楚的是，GNN网络所完成的工作是什么。

当我们将一个待处理的句子进行字符或者词语切分后，得到token序列，并初始化表示，经过CNN、LSTM、BERT等模型后，得到的是增强的token表示，这一表示融合了词法、句法等上下文信息。这也窥视为什么我们可以直接获取bert倒数第二层的输出，再将所有词的向量做平均，作为整个句子的向量表示。

因此，当token序列变为一个图结构时，每个token成为图中的节点，token之间的共现或者依存等关系成为图中的边时，利用GNN模型进行特征提取完成的其实也是token节点特征的增强，即对应增强的节点embedding表示，同样的可以根据节点embedding，通过图中节点embedding的pooling等操作，得到整张图的表示。

进一步的，我们发现，无论是序列结构，还是图结构，其在增强token表示的过程，实际上是融合上下文信息的过程。以CNN为例，其通过滑窗的方式，学习到的是制定n-gram的共现信息(其中的n取决于卷积核的大小)，LSTM学习的是上文之间的依赖关系，双向LSTM建模的是上下文之间的关系。这种上下文的获取是很直接的，可以是整个句子，也可以是指定的窗口。

但对于GNN而言，对应的token的上下文则是其一阶邻居或者二阶邻居，将邻居的特征融入到该token上的方式很直观的想法就是不同邻居的特征，按照不同的贡献度(权重)，联合自身的特征进行加权求和，像能量传递一样，传递给当前token，并得到该token的总体能量表示。这也就是常说的聚合操作。

因此，为了实现上述过程，我们至少需要有以下几个输入：

我们需要针对每一个节点，再每次特征聚合时，都拿到一阶邻居和自身信息。这就用到了就邻阶矩阵。

1、每个token节点的特征信息，即特征矩阵X。就像CNN的输入一样，我们针对每个词，可以通过lookup embedding的方法获取每个词对应的embedd表示(通过word2vec训练得到)，可以是100维、300维等。当然也有其他的特征表示方法，如收集特征，然后对应的获取指定特征项上的值。

2、每个token的上下文信息，即邻阶矩阵A。图的上下文信息通过邻接矩阵(记录了每个节点对应的邻居信息)实现，而为了获取自身的信息，需要添加一个自环操作，即邻接矩阵+对角矩阵(对角线值为1，其余为0)。

3、上下文贡献信息，即度矩阵D。上面说到当前节点token，其接受到其上下文节点的信息，但需要有不同的权重，这个权重比较直观的想法就是借助当前节点的邻接个数来说，如果邻接个数多，那么每个对应的节点开源所贡献就会被分解，因此，可以通过计算每个节点对应的邻居个数，得到一个度矩阵，然后再求倒数(取逆)，得到对应的值。而对于度数很大的超级节点，其值趋近于0，所以通常也会先对度开根号，然后再取逆。

因此，很自然的，有了上述三个矩阵，做一个连乘，即D*A*X，将token节点的特征矩阵，通过邻阶矩阵获取上下文节点及其对应的特征，再乘以根据对应的权值，就完成了可以将每个token节点一阶邻居在相同维度上的特征值进行聚合(最简单的是直接相加)。

进一步的，我们将这一过程纳入神经网络当中进行拟合学习，需要用到一个参数矩阵W，一个激活函数，如Relu，得到经过一层GNN后得到的节点隐藏状态表示H。

当然，这是比较朴素的方法，在实际的工作中，会使用归一化后的邻阶矩阵进行处理。

二、从CNN到GCN

1、从CNN到GCN

说到GNN时，我们一定会想到GNN，两者之间存在很大的共性，例如下图中展示了卷积神经网络的特征提取过程：

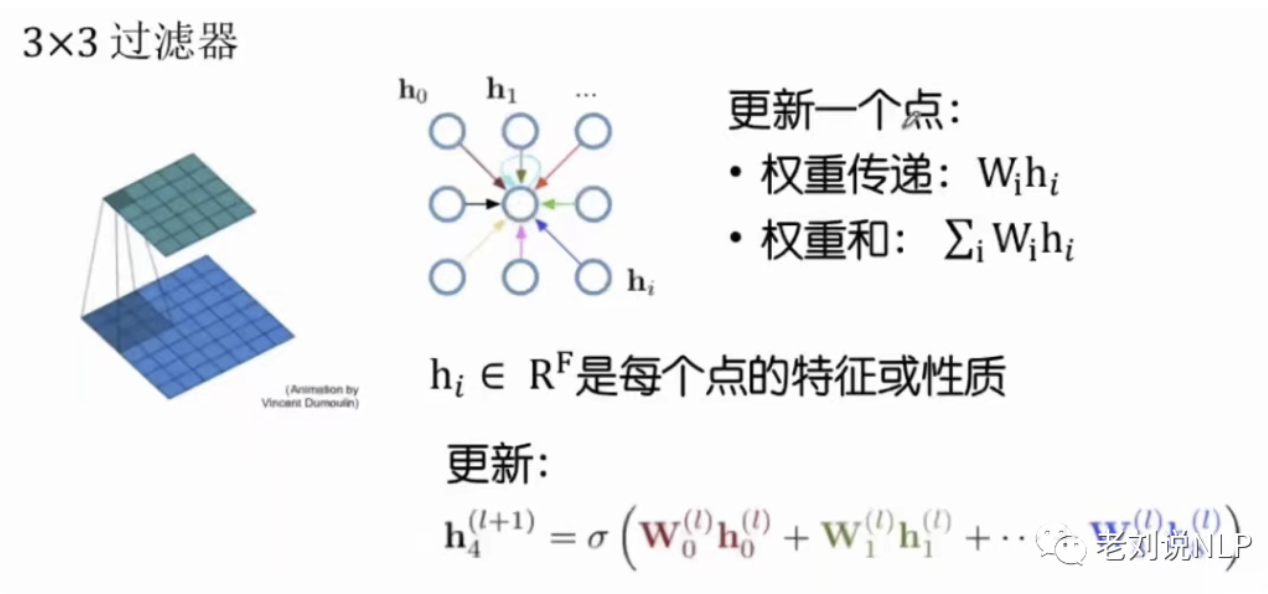
卷积神经网络可以被看做一种特殊的图卷积神经网络，在使用 3*3 的卷积核提取图像信息时，将中心节点周围的八个邻居节点及其自身的信息聚合起来，可以得到该节点新的表征。不过，CNN 中，每个节点与中心节点在信息聚合时的权值W是可以通过学习得到的，而 GCN 中节点之间的聚合权值由每个节点的度决定。

GCN是图神经网络中的一个典型代表，考虑自身特征：所以原始的邻接矩阵上+一个单位矩，并进行归一化操作，归一化操作：对与每一对相连的2个node分别处以各自度的个数。

 

2、GCN的构造

在无向图G中，我们将节点集合定义为 V，其节点个数为 n；边集为 E，其节点个数为 m。其中存在几个概念：

 

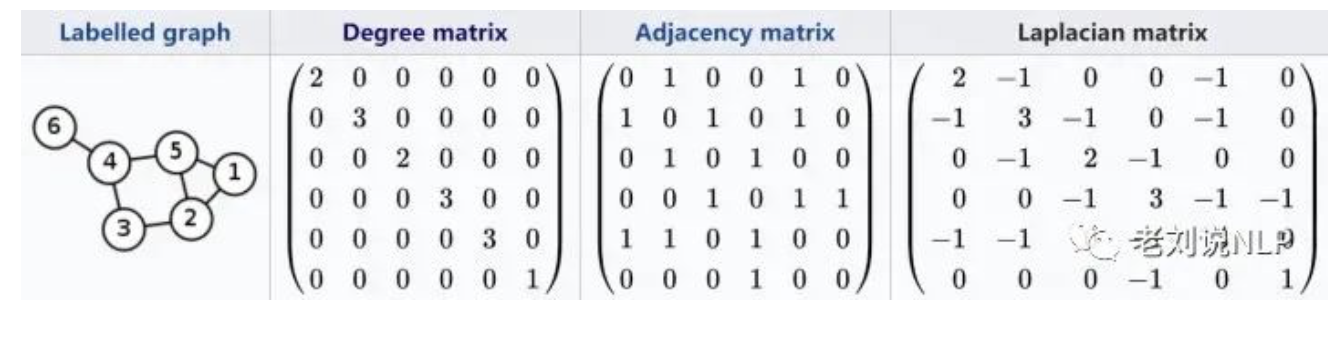
1）邻接矩阵A

若节点 i 和节点 j 之间存在连接关系（边），则邻接矩阵 A 中对应的元素值为 1，否则该元素的值为 0， A 为一个对称矩阵。

2）加上自环的邻接矩阵

为了在后面进行聚合时，能够叠加自身的特征，需要在邻接矩阵的基础上再加上一个单位矩阵。

3）度矩阵D

度矩阵 D 为一个对角矩阵，第 i 行对角线上的元素为节点 i 的邻居节点的数量。

4）归一化后的拉普拉斯矩阵

归一化后的拉普拉斯矩阵为单位矩阵与归一化后的邻接矩阵之差，常用的拉普拉斯矩阵实际有三种：

普通形式的拉普拉斯矩阵L=D−A

 

对称归一化的拉普拉矩阵L=D-1L=D-1/2AD-1/2

 

随机游走归一化拉普拉斯矩阵L=D-1A 

5）归一化后的邻接矩阵

由于在建模的过程中，大的节点在其特征表征中将具有较大的值，度小的节点将具有较小的值。可能会导致梯度消失或梯度爆炸，也会影响随机梯度下降算法。具体操作为：归一化后的邻接矩阵 为邻接矩阵 A 分别左乘、右乘，其中度矩阵对角线上的元素为度矩阵 D 对角线上每个对应元素开根号、取倒数后的结果。

3、GCN具体实例

下面以一个具体的例子来说明：

以上面该图为例，图中共有1、2、3、4四个节点，(1,2)、(1,3)、(2,3)、(3,4)共4条边 。

可以分别得到邻接矩阵A:

为了能够聚合自身的信息，需要在某个节点上加上一个自环，即添加一个对角矩（对角线的值为1，其余为0）：

在此基础上，可进一步得到度矩阵D波浪：

对度矩阵进行归一化，取每个值的-1/2次方：

进一步的，对邻接矩阵进行归一化处理，可以得到如下结果：
4、GCN的模型构造
GCN模型的构造如下，包括输入层、隐藏层与输出层，以归一化的邻阶矩阵A波浪和节点特征矩阵H作为输入，通过一个参数矩阵W，在隐藏层中进行特征的聚合，得到增强后的节点特征表示。

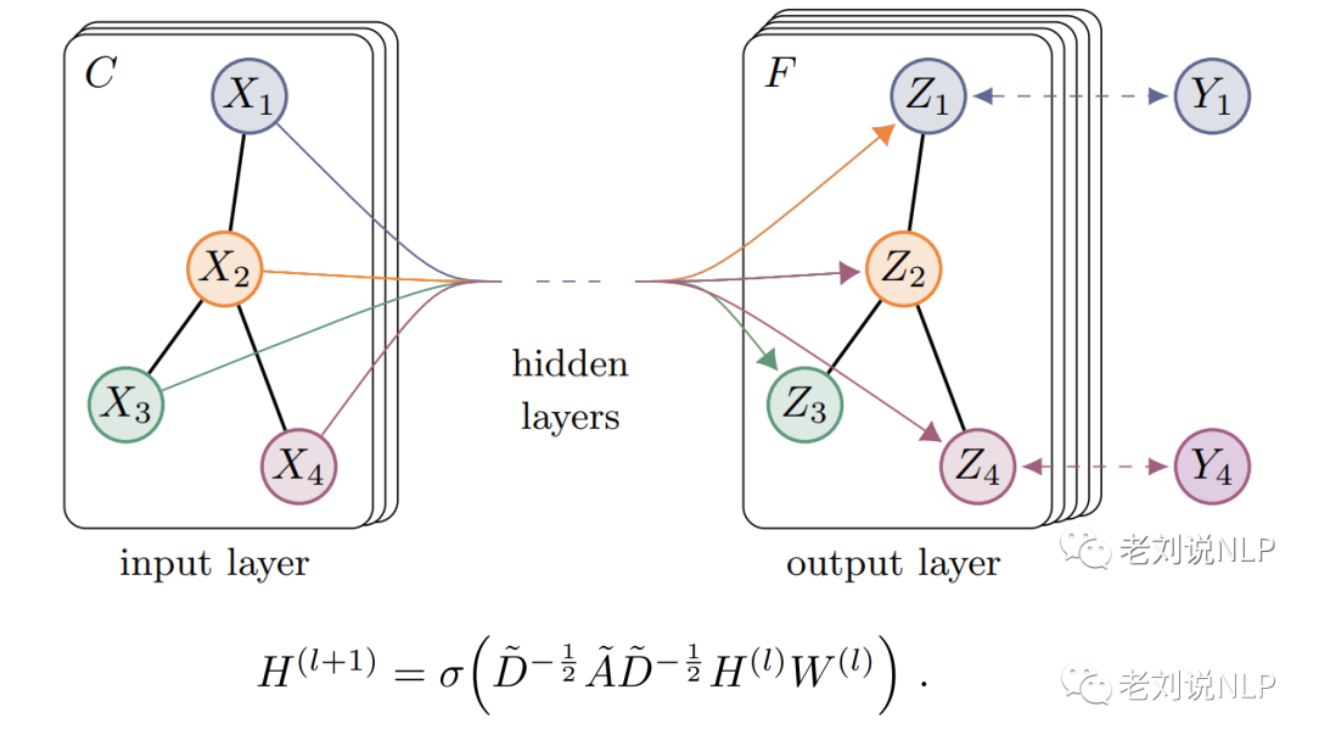
在输出层中，通过对第一层的特征值进行ReLU函数非线性激活，再经过一层的聚合后，接入softmax层做分类，完成后续的节点分类任务。

其中：

               

一个两层GCN的例子阐述GCN是如何对节点进行分类的，令。根据逐层传播公式，这个两层的GCN输出embedding。
这里，是权重矩阵, 目的是对节点的输入embedding做线性变换(从输入层到隐藏层的变换)。是另一个权重矩阵，目的是对第一层变化后的节点embeding再做一次变换(从隐藏层到输出层)。

三、从GCN到GraphSAGE

1、GCN网络的不足

 

如上一节所说到的，GCN的思想十分直观，利用其全局的邻接矩阵来获取中心节点的邻居节点，然后通过参数矩阵W来拟合网络，以得到增强的图节点表示。不过，GCN存在明显的缺点，例如：

1）全局采样耗内存

GCN在训练阶段它的信息传播是在包括训练节点和测试节点构成的整张图上的，在邻居聚合时，没有进行采样，所以每次聚合都需要整张图的邻接矩阵，也就是说每一轮的迭代都要对全图的节点进行更新，当图的规模很大时，都需要将整张图放入内存，也十分耗时，难以扩展到大规模网络。

2）聚合方式简单朴素

GCN中，是直接把邻居的特征进行求和，跟节点特征矩阵中的向量相乘之后，相当于是“求平均”。

3）无法快速获取新节点表示

这个新的节点表示，指的是旧节点的新表示以及新节点的表示两种。GCN中每次学到的是每个节点的一个唯一确定的，如果要产生新的表示，需要从头开始训练。实际上，当前很多情况下，图的结构都会发生演化，当网络结构改变以及新节点的出现，GCN都需要需要重新训练，成本很高，会偏很难落地在需要快速生成未知节点表示的业务上。

 

2、从GCN到GraphSage

针对以上几种问题，尤其是为了解决在图结构发生变化，有新的未知节点出现的情况下，得到节点表示，通过邻居随礼抽样聚合信息的方法。Graphsage被提出，其通过采样固定的k个邻居，可以不输入整张图，可以使用不同的聚合函数（mean、maxpooling、lstm等），可以预测新的节点，但未考虑不同邻居的重要性。

首先，针对全局采样耗内存的问题，GraphSAGE在训练阶段的信息传播只在由训练节点构成的图中进行，并且对邻居进行了采样，采样方式将GCN的全图采样优化到部分以节点为中心的邻居抽样，这使得大规模图数据的分布式训练成为可能，并且使得网络可以学习没有见过的节点。这样一来，不再是学习每个节点的表示，而是学习一系列聚合函数，这样每次聚合只需知道邻居节点的信息，而不需要把整张图的邻接矩阵都加载到内存。

其次，针对聚合方式简单朴素的问题，GraphSAGE进一步拓展了聚合的方法，提出了LSTM、Pooling等聚合方式，不是简单地求平均，而是更加复杂的组合方式。

最后，针对无法快速获取新节点表示的问题，对于新加入的节点，通过获取该节点的邻接信息，通过之前训练好的聚合函数聚合邻居信息学习到节点的表示。实际上，在增加了新的节点之后，旧的节点也需要更新，这个是无法避免的，对于老节点，可能新增一个节点对其影响微乎其微，所以可以暂且使用原来的embedding，但如果新增了很多，极大地改变的原有的graph结构，那么就只能全部更新。所以说，这个只是降低了全部更新的频率。

 

3、Graphsage的处理逻辑

GraphSAGE(Graph SAmple and aggreGatE)的思想是通过一个aggregate function学习到节点近邻的信息的综合，与自身上一步骤的信息concat变换后得到该节点新的信息。就是不断的聚合邻居信息，然后进行迭代更新。

随着迭代次数的增加，每个节点的聚合的信息几乎都是全局的，这点和CNN中感受野的思想类似。

它的流程大致分为3步：

step1：对邻居进行随机采样，每一跳抽样的邻居数不多于 Sk个，如图第一跳采集了3邻居，第二跳采集了5个邻居；

steep2：生成目标节点的embedding：先聚合二跳邻居的特征，生成一跳邻居的embedding，再聚合一跳的embedding，生成目标节点的embedding；

step3：将目标节点的embedding输入全连接网络，得到目标节点的预测值。

 

更形象地，

 

红色节点的更新拿到了它一、二跳邻居的信息，那么网络层数就是2。为了更新红色节点，首先在第一层()会将蓝色节点的信息聚合到红色节点上，将绿色节点的信息聚合到蓝色节点上。随后，在第二层()红色节点的embedding被再次更新，这次用的是更新后的蓝色节点embedding，这保证了红色节点更新后的embedding包括蓝色和绿色节点的信息。

 

4、Graphsage的实现流程

在具体实现上， 我们可以参考其伪代码来了解下：

第一行：初始化节点嵌入，初值为节点的特征向量；

 

第二行：第一层 for 循环，遍历图的深度，可以理解为神经网络的层数，循环K次聚合，第k次的循环代表聚合的是第K跳邻居，如K=1代表目标节点的相邻节点，K=2代表相邻节点的相邻节点；

 

第三行：第二层 for 循环，是某一层图中的所有节点，并聚合指定数量的邻居，N(v) 代表在v的邻居中以固定size采样的节点集合。即GraphSAGE中每一层的节点邻居都是是从上一层网络采样的，并不是所有邻居参与，并且采样的后的邻居的size是固定的；

 

第四行：从上一层神经网络中利用聚合函数聚合当前节点邻居的特征。其中，因为邻居没有顺序，聚合函数需要满足排序不变量的特性，即输入顺序不会影响函数结果，所以GraphSAGE对比采用了若干种邻居聚合的方式：

 

1）平均聚合：先对邻居embedding中每个维度取平均，然后与目标节点embedding拼接后进行非线性转换。

2） 归纳式聚合：直接对目标节点和所有邻居emebdding中每个维度取平均后再非线性转换：

3）LSTM聚合：先对邻居随机排序，然后将随机的邻居序列embedding 作为LSTM输入。

4）Pooling聚合：先对每个邻居节点上一层embedding进行非线性转换，等价单个全连接层，每一维度代表在某方面的表示，再按维度应用 max/mean pooling，捕获邻居集上在某方面的突出/综合的表现以此表示目标节点embedding。

 

第五行：将当前节点的特征和邻居特征拼接并经过一个全连接网络得到当前节点的新特征；

 

第七行至第八行：对特征进行归一化，并通过 K 层 GCN 后进行输出，进行拟合。

 

5、Graphsage的损失

此外，在拟合损失函数上，包括有监督的损失和无监督的损失两种：

1）基于图的无监督损失：节点u与“邻居”v的embedding也相似，而与“没有交集”的节点不

如果节点u和v在实际图中接近，则它们的节点嵌入在语义上应该相似，期望z_v和z_u的内积很大，如此大的数值输入到sigmoid输出会接近1且log(1)=0；

2）基于图的有监督损失：有监督损失常后接一个具体的学习任务，例如节点分类，一个比较简单的方案就是对每个node的embedding接一个全连接层，就得到了一个损失函数。

四、从GNN到GAT

如上一节所说到的，GCN的思想十分直观，利用其全局的邻接矩阵来获取中心节点的邻居节点，GraphSAGE解决了GCN存在的三个问题，能够较好的在大图上进行预算，但其未考虑不同邻居的重要性。因此，随着atterntion的兴起，研究人员提出了一种基于attention的节点分类网络GAT。

 

GAT的基本思想在于，根据每个节点在其邻节点上的attention，来对节点表示进行更新。在进行邻居特征聚合时，利用mask机制来筛选邻近的节点，引入attention来学习分配权重。

 

其中，attention通过图注意力层来实现，对节点对  ，注意力系数计算方式为：

1)  是节点  到  的注意力系数，  表示节点  的邻居节点。

2)节点输入特征 ，其中  分别表示节点个数和特征维数。

3)节点特征输出是 

 是在每一个节点上应用的线性变换权重矩阵， 是权重向量，可以将输入映射到。最终使用softmax进行归一化并加入LeakyReLU以提供非线性性质。

五、总结

本文主要介绍了图神经网络相关的内容，以从序列神经网络到图神经网络为切入点，逐步讲述从CNN到GCN，从GCN到GraphSage，从GCN到GAT三个方面的内容进行了论述。

 

实际上，我们可以发展，图神经网络的核心就在于如何进行上下文构造以及上下文特征聚合，上下文构造上，无论是游走方式，还是随机采样方式，本质上还是要依托邻接矩阵。在特征聚合上，重点在于不同邻居特征的权重分配以及信息选择。

 

进一步的，我们可以想到的是，图神经网络的处理对象是复杂的，就一个图而言，其可以用到的信息包括图的节点特征、图的图谱结构特征、图的边特征(包括边的方向，边上的权重，边上的属性等)，将这些信息进行有效整合，是个很有趣的问题。后面，作者将对这些方向的内容进行总结。

 

参考文献

1、https://www.jianshu.com/p/eaa69644b7b0

2、https://mp.weixin.qq.com/s/rytzS0yTUr_BpO7XBinQiw

3、https://mp.weixin.qq.com/s/cGkd_7I9KPsXTL8uO8Lfuw

4、https://zhuanlan.zhihu.com/p/74242097

5、https://proceedings.neurips.cc/paper/2017/file/5dd9db5e033da9c6fb5ba83c7a7ebea9-Paper.pdf

6、https://mp.weixin.qq.com/s/7LfJ8wDr4K6cVunb8Q_83g

7、https://mp.weixin.qq.com/s/LrAjuJyzrXWAGvvTLTNd8Q