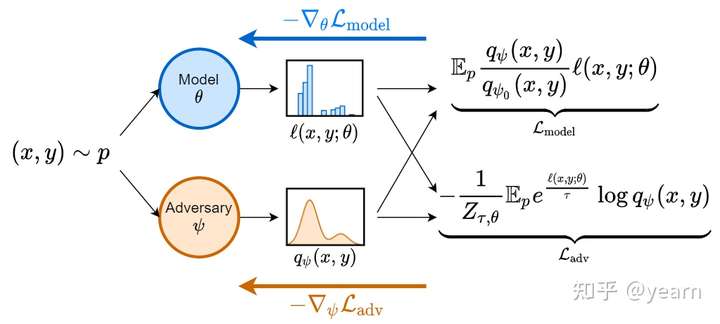
常见的算法使用经验风险最小化(ERM)的范式,有一个模型参数为,一个损失函数
和数据分布
,通常情况下我们只能看到训练数据分布
,那么ERM可以写作
当测试数据集的时候,ERM往往性能会大幅度下降。Distributionary robust optimization(DRO) 为这个问题提供了一个解决方案,即在一个预先确定的分布族
(uncertainty set)中,用最糟糕的预期风险替换一个单一分布下的预期风险。
如果包含了
,那么DRO的目标函数就会成为
上平均损失的上界。然而我们不总是能得到域的分布,即将
划分为多个分布
,当我们没有domain的先验知识的时候,如何去构造
是DRO成功的关键,目前大概有如下几种方式
- 基于 moment constraint,对数据分布的一阶矩,二阶矩进行约束。这种方法需要从数据中估计一阶矩,二阶矩,目前只能在比较toy的数据集上使用。
- 基于
divergence
- 基于 Wasserstein/MMD ball
- 基于 coarse-grained mixture models
- 基于
divergence的方法
本文通过几篇高引和最新的顶会文章对DRO进行简单介绍
基于 ![[公式]](https://www.zhihu.com/equation?tex=f-) divergence的方法
divergence的方法
开篇之作:Kullback-Leibler Divergence Constrained Distributionally Robust Optimization
由于年代比较久远,文中使用的notation和我们现在的稍有差别,其对DRO的定义为
这里的是参数集而
是
的数据分布,
作为uncertainty set。本文第一次采取了如下方法来定义uncertainty set,其中
是KL散度,
是我们对真实数据集的估计。
这里的超参数控制了uncertainty set的大小。我们知道KL散度隐式的假设了
相对于
是处处连续的,并且他可以写作
到现在为止,我们内层的优化目标是概率分布,而
并没有在目标函数中出现,这就很难优化。作者采用了change-of-measure的技巧,首先我们记
为似然比(likelihood ratio),也称之为迪姆导数(Radon-Nikodym derivative),我们可以轻易的得到
,然后使用change-of-measure将KL散度转化为
同样地,对目标函数使用change-of-measure的技巧,我们可以得到
这样的话内层优化就从依赖于的优化问题转化成了对于
的
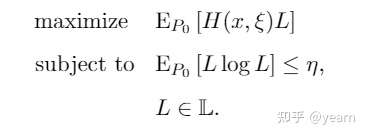
因为本文关注于凸优化的场景,也就是说是凸集,
是凸函数,作者根据一定的假设,直接推出了内层优化的闭式解
这里的是Lagrangian multiplier。内层优化有闭式解意味着什么?意味着我们这个worst-case distribution有闭式的概率分布,根据
的定义,我们只需要找到使得内层优化最大的
然后乘上
即可,因此我们可以得到
如果我们在外层优化找到了最优的,那么他的概率测度可以写作
这是一个非常有趣的现象,内层优化的最优分布和数据分布成正比,比例因子为
.
所以这个bi-level的优化问题直接变成了单层的优化问题
ICLR 2021: Modeling the second player in distributionally robust optimization
本文使用生成模型对uncertainty set进行建模。但是不是所有的生成模型都可以表达有用的数据分布(如果太大就会有噪音数据),因此文中使用KL散度约束模型分布与真实数据分布之间的距离,文中提出的Parametirc DRO如下所示
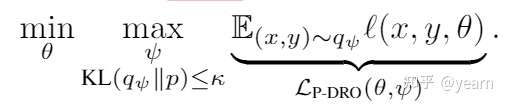
他的优化过程比较麻烦主要有两个注意点
难以保证学到的数据分布真实
因为外层分布的优化是基于一个良好的数据分布的,我们不能保证
是有效的数据分布,因此作者将该问题转化成了一个importance sampling的问题,这样保证了数据点
是从真实数据中采样得到的。
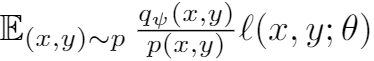
不过真实数据分布我们依然不知道,因此还需要去估计他,这个estimator靠如下方式得到
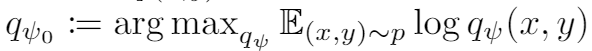
即在所有生成模型中选择一个对数似然估计的最准的,那么接下来模型变成了如下形式,这就是一个简单的加权损失函数,为了训练的稳定,在一开始的时候是一样的,也就是ERM。
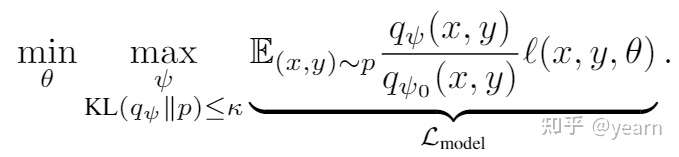
生成模型的训练过程
要最大化上述损失有两个难点
- 这个KL ball的限制难以达到。
- 最大化这个期望会导致训练的不稳定(large gradient variance)。
为了解决这个问题,作者首先将KL散度使用lagrangian松散一下
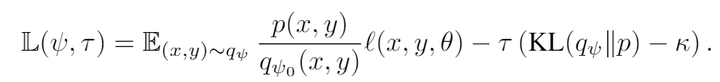
作者证明了
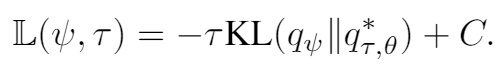
其中
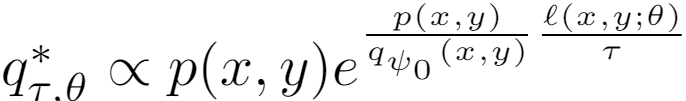
于是巧妙地将这个最大化期望损失的问题转换成了最小化两个分布的KL散度,其中依赖于真实数据分布
,这是我们无法得到的,因此作者将这一项看作常数,再经过一系列转换变成了
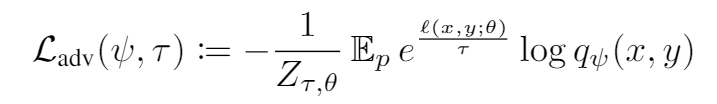
整体的model记作
基于 Wasserstein/MMD ball
这一块推荐两篇文章都非常的硬核,在这里只陈述他们大概的思路
Wasserstein ball-based: ICLR 2018 Oral: Certifying Some Distributional Robustnesswith Principled Adversarial Training。
同样,先拿出DRO的优化目标
不确定集的选择影响了模型的鲁棒性和可计算性。他们的方法大概总结如下:对一个将数据点
扰动到
的扰动器,我们规定一个cost function:
,通常情况下
。考虑一个鲁棒性区域
是一个数据分布
附近的
-ball,
是Wasserstein metric。直接解决这个bi-level的问题是非常难的,因此作者使用拉格朗日乘子对问题进行简化并重新公式化为
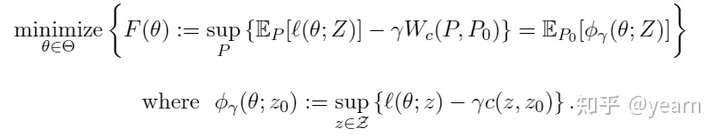
式子中的可以控制对抗攻击的强度。
训练的算法其实是非常简单的,只不过文中涉及了对算法性质比如鲁棒性,收敛性的大量证明,感兴趣的读者建议深度阅读原文。

MMD-based: NeurIPS 2019:Distributionally Robust Optimization and Generalization in Kernel Methods
本文首先提出了以往方法的两种缺陷
- 基于
-divergence的uncertainty set只能包含真实数据分布附近的数据点,不能偏离真实数据分布太多,因此很难使得worst-case distribution
包含测试分布,所以不是很能保证一个很好的泛化性能。
- 基于Wasserstein distance的uncertainty set包含了一个连续分布,克服了上述问题,但是这种方法非常难以实现,并且理论过程需要复杂的假设。
本文使用MMD(maximummean discrepancy)对uncertainty set进行建模,得到了MMD DRO。亮点有三
- 本文证明了MMD DRO等价于ERM加上一个对损失函数的希尔伯特范数的惩罚项。
- 在Gaussian kernel ridge regression的场景下,作者证明了一个新的泛化损失上界。
- 作者给出了近似的易于实现的算法。
首先两个数据分布之间的MMD (max min discrepancy)距离定义如下,不了解MMD的可以点击这里
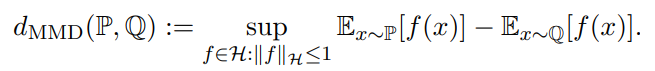
我们定义均值embedding为,那么MMD可以写作
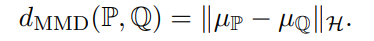
到这里我们就可以定义本文的核心问题了 MMD Dro:
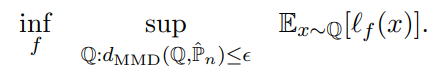
这里的是一个有
个样本点的经验数据分布。接下来使用
表示DRO的uncertainty set,这是一个包含经验数据分布的分布,
是从uncertainty set中采样的分布,
表示真实数据分布。如果
半径足够大,那么它就更有可能包含真实数据分布。但是半径太大这个问题又会很难处理(包含很多噪音样本),作者给出了如下两个定理来对泛化性能的bound进行讨论
Lemma 1. 对于一个有上界的核函数,有
的概率下式成立:
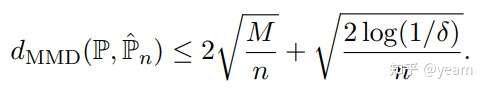
这里是样本数目,显然样本数目越多
更有可能逼近真实数据分布。
Corollary 1. 如果我们设置,那么我们有
的概率使得下述的bound成立
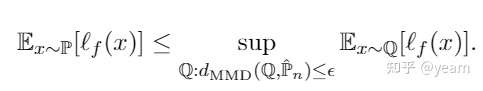
本文称右端的式子为DRO的对抗问题,接下来会对这个对抗问题进行bound。
现在引入额外假设,此时risk
可以写作内积的形式
,那么我们就可以得到
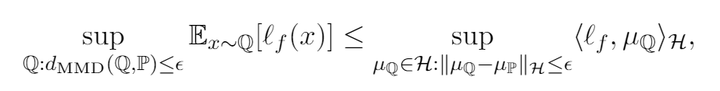
之所以这里是一个不等式,是因为不是所有空间内的函数都是某些分布的mean embedding。上述形式下,我们的分析就会变得更加容易些
Theorem 1. 假设,那么下述不等式成立:
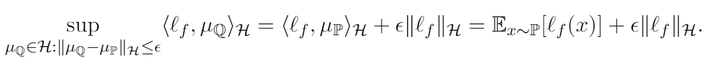
可以看到直接把MMD整没了,那么我们总体的DRO就转化成了
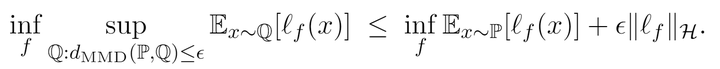
回顾一下Lemma 1.,右端内层的优化是真实数据分布empirical loss的上界,所以最终的优化目标体现了这样一个事情:只要在经验数据分布上优化
,再加上对
的一个范数的优化,就有大概率能够提供一个bound给分布外的数据。当然了,上式并不是完全体,因为我们不能保证
,所以作者还进行了进一步的推论,对这一项正则项进行近似,最终将对loss的penalty转化为了对
的
有意思的是,本文还将MMD DRO进行了另一个角度的解释,因为搜索所有在MMD ball中的分布是非常难做到的,因此作者将问题进行化简,只关注和经验分布
具有相同support的分布(直观来看也就是含有相同的样本但权重不一样)
,那么MMD DRO问题可以简化为
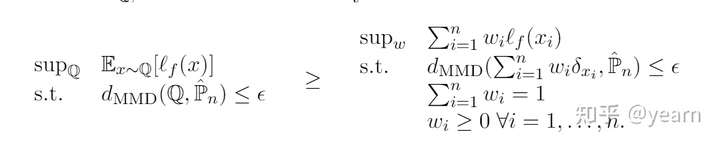
进一步的,作者验证了这个简化版的问题的最优解为
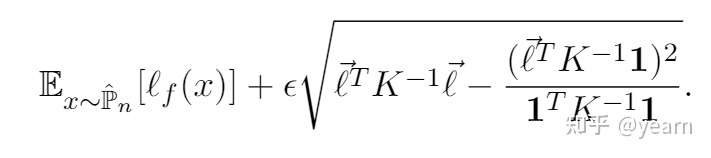
其中是高斯核矩阵,
姑且当作是
就好,巧妙的是,当我们将高斯核矩阵设置为identity
的时候,这个式子就变成了
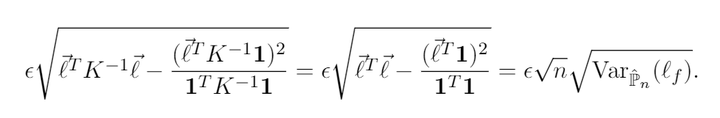
也就是说,我们从MMD DRO出发,其实得到了常用的empirical variance penalty,这里的方差在以往工作中定义为
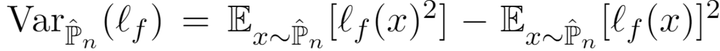
Coarse-grained mixture models
EMNLP 2019: Distributionally Robust Language Modeling
本文关注的场景是NLP下的,但是对于CV,ML也很有借鉴意义。现在的语言模型都是大大数据集上进行训练的,而训练数据集有非常多的主题(新闻,评论等),而测试的数据集往往是未知的。那么我们能否训练一个通用模型在所有测试数据集上表现良好呢?本文提供了一种思路
首先,使用MLE会失败!为什么?虽然数据越多越好,但是如果训练过程中用的数据与测试无关,那么测试效果会下降(测试,训练数据都是新闻时,增加评论相关的训练数据就是使得模型效果下降),而这个下降的原因是:MLE强调的是在训练数据中的平均效果,从而忽略了出现次数比较少而重要的数据。考虑我们的数据集10%是评论,90%是新闻,那么MLE就会把重点放在新闻上,而我们需要的是将这个关注”搬回来“,让模型对两种数据同样重视。
我们先来看一看问题的建模,数据,训练数据分布,测试数据分布记为。语言模型
通常使用如下的MLE损失被训练去近似训练数据分布
当测试训练数据独立同分布,传统的统计理论告诉我们只要数据够多,MLE就能效果卓越。但是测试数据分布往往可能是训练数据中很少的一部分(上述例子中的评论),这时MLE就会效果极差。
这时我们定义一个潜在的测试数据分布集合作为uncertainty set,如果一个模型在
中表现很好,那么他也能在
中表现良好。而DRO的关在在于uncertainty set和loss,作者分别对这两个关键点进行了设计。
Uncertainty Set: 本文的uncertainty set定义为如下形式
也就是说是
的集合,而
们组成了训练数据
。为了在所有可能的测试集上表现良好,我们的训练目标变为
这个目标可以通过upweighting损失比较大的数据来实现在所有测试分布上的一个比较均匀的表现。(这也是 mixture models和之前几种模型的核心差距,个人理解mixture models更像是data-centric的方法,对自身数据进行mixture或者reweighting从而获得更好的鲁棒性。)
上式有一个致命的缺陷,他约束的是任意分布,如果有一个sample是噪音数据,那么模型将会给他分配很高的权重。为了解决这个问题,作者提出了要将uncertainty set约束到有效分布上而不是任意分布。有一个方法可以避免这个问题:”我们不要逐sentence进行加权,我们根据topic进行加权“。
作者假设每个句子都属于一个topic ,那么句子分布记作
。这时我们将上述的uncertainty set和worst case topic distribution分别进行改写
这一方法通过调整topic之间的权重来取得一个较为均匀的表现。
本文对于uncertainty set的loss形式如下:
那么加上MLE loss,我们的总体损失函数可以写作如下形式
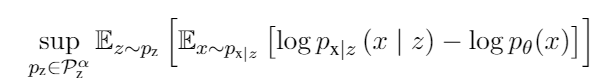
也就是说训练模型来匹配每个可能的测试分布
,使每个density尽可能一致。可以还是难以理解,那我们对比一下
不同之处在于可以看作一个常数,但是
依赖于
因此对于外层优化而言不能看做constant。
Algorithm 现在难点在于这一项不好处理。本文对每个topic训练一个模型
然后用以估计这一项的值
。整体优化的思路分两步
- 在多个step中选择使得总体损失最大的
,即我们存储到第
次优化时每个topic产生的平均损失(通过exponential weighted moving average)
,然后选择使得该loss最大的
:
。
- 有了
,我们就可以根据下式更新参数,这里的
是我们对概率分布
的估计。
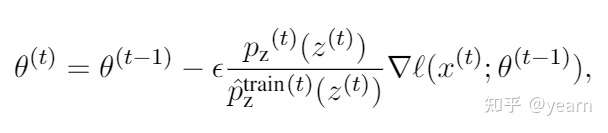
这时候就有人会问了,这个难道真的要遍历所有排列组合吗?其实不用,我们只需要将
从高到低对所有topic排序,然后依次赋予
的概率值。举个栗子
给定,
,那么
。第三个topic因为loss最大,所以赋予了
的概率值,而第一个topic loss第二大,但此时
,不够分,所以把剩余的概率都给他,topic 2没有概率。这时上面对梯度的权重就变成了
。
ICML 2018 Oral: Does Distributionally Robust Supervised Learning Give Robust Classifiers
先说结论,本文之所以能作为oral出现,他的intuition非常关键,本文依然选择KL-divergence作为uncertainty set的建模工具,但是抛出了一个重磅结论:DRO训练得到的分类器并不比ERM的好! 我们必须添加一些结构化的假设,引入domain相关的信息(gender,style等)才能真正超越ERM,训练出robust classifier。
先来看看本文的建模,是density ratio,
则为
divergence,第一个约束就是uncertainty set和empirical distribution
之前的divergence,将这个density ratio作为权重对所有样本重新进行加权,第二个约束说所有权重的和为1。
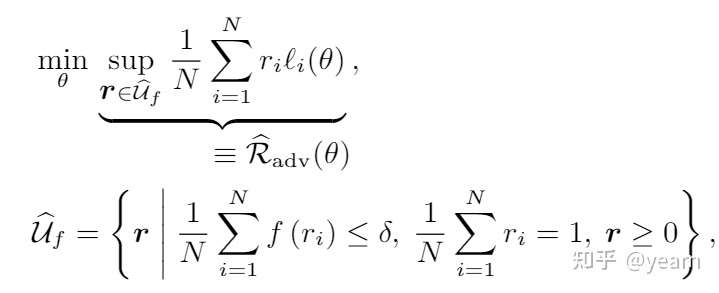
最后,欢迎大家关注github,聚合了OOD,causality,robustness以及optimization的一些阅读笔记
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢