一 协同过滤方法
1.1 论文
论文题目:《Amazon.com recommendations item-to-item collaborative filtering》2003 IEEE Internet Comput
论文地址:《Amazon.com recommendations item-to-item collaborative filtering》
(
协同过滤是早期推荐系统的首选方法,分为从物品相似度角度(ItemCF)和用户相似度角度(UserCF)出发的协同过滤方法。
对于协同过滤简单的理解是:如果张三和李四同时喜欢A,B,C物品,李四还喜欢D物品,那么可以认为张三也喜欢D物品(UserCF)。
UserCF有个问题是:如果无法获取到过多用户对物品的反馈信息,这会导致用户的历史数据向量往往是非常稀疏的,对于只有几次购买或点击行为的用户来说,寻找其相似用户很难。
以Amazon为代表的(这篇文章)使用的是ItemCF的方式,通过计算用户-物品交互矩阵中物品列向量之间的相似度,得到物品之间的相似矩阵,然后找跟当前用户喜欢的物品最相似的物品,推荐给用户,从物品的角度出发
)
推荐算法在电商网站中被广泛使用,它利用输入的用户兴趣,生成一个物品列表推荐给用户。以往的推荐算法只是利用用户购买的物品信息或者用户进行了评分的物品去推断用户的兴趣,但其实可以结合其它更多的信息,比如物品自身的信息,用户的统计特征等进行用户兴趣的推断。在亚马逊,我们利用推荐算法为每一个用户提供个性化的服务。
电商中的推荐算法面临以下几个问题:
- 用户和物品的数据量庞大
- 推荐算法需要快速、及时的生成推荐列表
- 对于一个刚使用应用的用户,关于他的信息是稀疏的(冷启动)
- 推荐系统要及时的捕捉到当前用户每个新操作中的信息
本文提出的是Item-to-Item Collaborative Filtering方法,即使在用户数据和物品数据量都很大的条件下,也能够迅速的生成推荐列表。
以往的协同过滤方法都是在寻找和当前用户最相似的用户,而本文提出的方式是寻找和当前用户购买过的物品最相似的物品。
衡量两个用户向量相似性的方法可以为
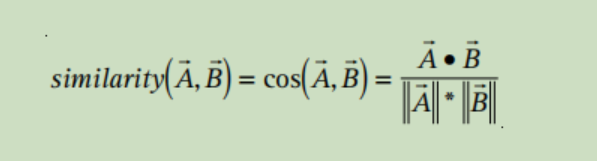
这种方式的计算复杂度大致是 ,M是用户数,N是物品数

如果系统中用户或者物品的数量很大,这个复杂度还是无法接受的。以往对这个问题的解决方法要么是删除掉那些稀疏的用户向量,或者删除掉那些不流行的物品等,这些方法都会在某种程度上影响推荐的准确率。
在本文之前有两种比较好的方法解决了计算复杂度的问题---cluster models和search-based methods.
cluster models首先利用无监督的聚类方法将用户进行聚类,这样用户就被分到了不同的类别,然后将‘寻找和当前用户最相似的用户’这个问题转换成一个分类问题---就是当前用户会最大概率的被分到哪个(聚类)簇中。这种方法减少了计算量,但是推荐准确率并不怎么高,因为很可能聚类在一个簇中的用户并不是真正相似的

search-based methods将推荐看作一个搜索问题,对于当前用户购买的物品,获取其关键词,然后搜索相关关键词的物品,推荐给当前用户

本文的Item-to-Item Collaborative Filtering方法

(
算用户-物品交互矩阵每个列向量之间的相似性,得到物品相似矩阵,然后推荐的时候根据当前用户买过的物品查它最相似的物品推荐给用户,文章最后亚马逊解释了自己为什么要用这种方式:
- 用户数远远大于网站中的物品数
- 用户的交互数据过于稀疏,快速寻找相似用户是不现实的
所以从物品的角度出发进行推荐
)
1.2 代码
Netflix数据集是一个电影评分数据集,包含480189个用户对于17770部电影的评分,推荐模型的任务就是从这些用户对于电影的评分中学习出用户的兴趣,根据用户的兴趣推荐相应电影给用户。
Netflix数据集包含以下几部分:
- movies_titles.txt:电影的描述信息,每一行包括---电影ID、上映日期、电影名字
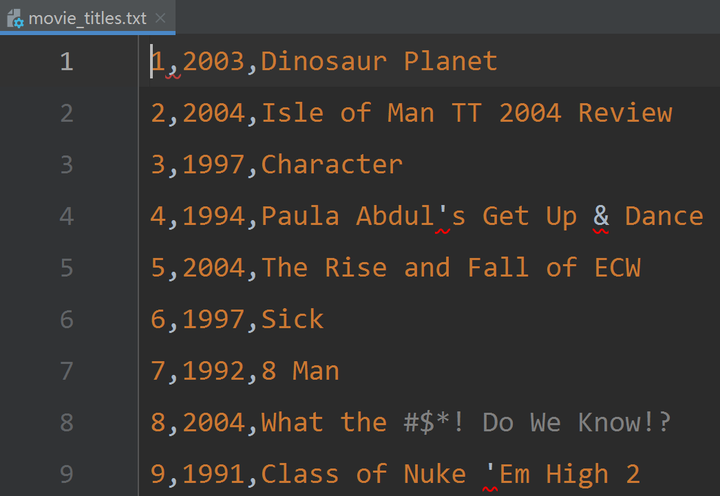
- training_set.tar:训练数据集,包含17770个文件,每个文件是用户对于相应电影的评分,文件第一行表示电影的ID,然后接下来的每一行包括-用户ID、用户评分、评分日期
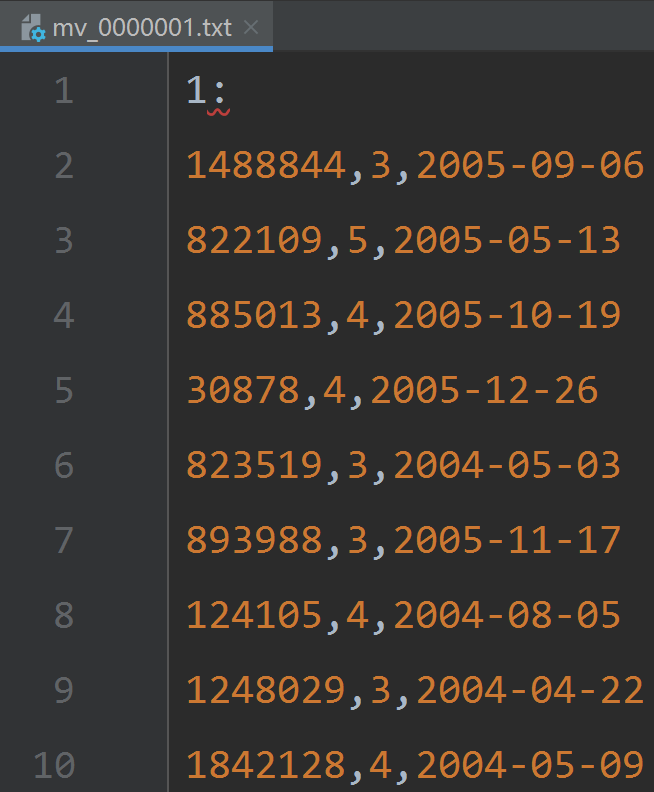
- qualifying.txt:验证数据集
- probe.txt:测试数据集
# coding=UTF-8
import os
import json
import random
import math
# 基于用户的协同过滤推荐算法
class UserCFRec:
# 初始化
def __init__(self, file_path, seed, k, n_items, K):
# 用户对电影的评分数据集路径
self.file_path = file_path
# 选取K个用户,只利用这些用户的评分信息进行推荐模型的训练
self.users_K = self.__select_K_users(K)
# 随机数种子
self.seed = seed
# 选取的近邻用户数
self.k = k
# 为每个用户推荐的电影数
self.n_items = n_items
# 训练集和测试集
self.train, self.test = self._load_and_split_data()
# 获取所有用户,并从中随机选取K个
def __select_K_users(self, K):
# train.json和test.json是指定的训练集和测试集
# 如果有的话使用指定的训练集和测试集
if os.path.exists("data/train.json") and os.path.exists("data/test.json"):
return list()
else:
print("随机选取K个用户!")
# 数据集中所有用户的集合
users = set()
# 获取所有用户
# 遍历训练数据集中每一个用户评分文件
for file in os.listdir(self.file_path):
# 获取文件名
one_path = "{}/{}".format(self.file_path, file)
print("{}".format(one_path))
# 打开每一个用户评分文件
with open(one_path, "r") as fp:
# 遍历文件中的每一行
for line in fp.readlines():
# 如果是第一行
# 是电影的ID
# 跳过
if line.strip().endswith(":"):
continue
# 否则是用户对于相应电影的评分
# 按照 ',' 分割出用户的ID
userID, _, _ = line.split(",")
# 添加进用户集合
users.add(userID)
# 随机选取K个用户
users_K = random.sample(list(users), K)
print(users_K)
return users_K
# 加载数据,并拆分为训练集和测试集
def _load_and_split_data(self):
train = dict()
test = dict()
# 如果指定了训练集和测试集
# 使用指定的训练集和测试集
if os.path.exists("data/train.json") and os.path.exists("data/test.json"):
print("从文件中加载训练集和测试集")
train = json.load(open("data/train.json"))
test = json.load(open("data/test.json"))
print("从文件中加载数据完成")
else:
# 设置产生随机数的种子,保证每次实验产生的随机结果一致
random.seed(self.seed)
# 遍历数据集
for file in os.listdir(self.file_path):
# 获取每一个电影评分文件
one_path = "{}/{}".format(self.file_path, file)
print("{}".format(one_path))
with open(one_path, "r") as fp:
# 第一行是电影的ID
movieID = fp.readline().split(":")[0]
# 后面每行是用户对于当前电影的评分
for line in fp.readlines():
if line.endswith(":"):
continue
# 以 ',' 分割每行
# 获取用户ID和电影评分
userID, rate, _ = line.split(",")
# 判断用户是否在所选择的K个用户中
if userID in self.users_K:
# 分割数据集
if random.randint(1, 50) == 1:
test.setdefault(userID, {})[movieID] = int(rate)
else:
train.setdefault(userID, {})[movieID] = int(rate)
print("加载数据到 data/train.json 和 data/test.json")
# 变为json格式
json.dump(train, open("data/train.json", "w"))
json.dump(test, open("data/test.json", "w"))
print("加载数据完成")
return train, test
def pearson(self, rating1, rating2):
# 计算两个用户之间的皮尔逊相关系数
# 是协方差除两个变量的标准差
# 计算用户之间的相似性
# rating1:用户1的评分记录,形式为
# {"电影ID1": 评分1, "电影ID2": 评分2, ...}
# rating2:用户2的评分记录,形式如
# {"电影ID1": 评分1, "电影ID2": 评分2, ...}
# 公式中的变量
# 自行查找一下'协方差简化计算公式','标准差简化计算公式'
sum_xy = 0
sum_x = 0
sum_y = 0
sum_x2 = 0
sum_y2 = 0
num = 0
# 如果两个用户同时对同一部电影进行了评分
for key in rating1.keys():
if key in rating2.keys():
num += 1
# 获取相应电影评分
x = rating1[key]
y = rating2[key]
sum_xy += x * y
sum_x += x
sum_y += y
sum_x2 += math.pow(x, 2)
sum_y2 += math.pow(y, 2)
if num == 0:
return 0
# 皮尔逊相关系数分母
# 两个标准差的乘积
# 上网查一下 '标准差简化公式'
# 就是下面这个
standard_deviation = math.sqrt(sum_x2 - math.pow(sum_x, 2) / num) * math.sqrt(sum_y2 - math.pow(sum_y, 2) / num)
# 分母不能为0
if standard_deviation == 0:
return 0
else:
# 分子是协方差简化公式,可自行查一下
return (sum_xy - (sum_x * sum_y) / num) / standard_deviation
def recommend(self, userID):
# 向userID进行推荐
# 获取跟当前用户最相似的用户
neighbor_user = dict()
# 获取训练集中的用户
for user in self.train.keys():
if userID != user:
# 计算皮尔逊相关系数
distance = self.pearson(self.train[userID], self.train[user])
neighbor_user[user] = distance
# 排序
# 获取最相似的用户
most_similar_user = sorted(neighbor_user.items(), key=lambda k: k[1], reverse=True)
# 要推荐的电影
movies = dict()
for (sim_user, sim) in most_similar_user[:self.k]:
for movieID in self.train[sim_user].keys():
movies.setdefault(movieID, 0)
# 累计评分
movies[movieID] += sim * self.train[sim_user][movieID]
recommended_movies = sorted(movies.items(), key=lambda k: k[1], reverse=True)
# 推荐电影列表
return recommended_movies
#基于物品的协同过滤推荐算法
class ItemCFRec:
def __init__(self, datafile, ratio):
# 用户对电影的评分数据集路径
self.datafile = datafile
# 测试集与训练集的分割比例
self.ratio = ratio
# 加载评分数据集
self.data = self.loadData()
# 分割数据集
self.trainData, self.testData = self.splitData(3, 47)
# 获取电影之间的共现矩阵
self.items_sim = self.ItemSimilarityBest()
# 加载评分数据到data
def loadData(self):
print("加载数据...")
data = []
for line in open(self.datafile):
# 评分数据集中每一行包含 用户ID 物品ID 评分 评分时间
userid, itemid, record, _ = line.split("::")
data.append((userid, itemid, int(record)))
return data
# 分割数据集
def splitData(self, k, seed, M=9):
# 0<k<M 分割参数
# M随机数上限
# seed随机数种子
print("训练数据集与测试数据集切分...")
train, test = {}, {}
random.seed(seed)
for user, item, record in self.data:
# 分割数据集
if random.randint(0, M) == k:
test.setdefault(user, {})
test[user][item] = record
else:
train.setdefault(user, {})
train[user][item] = record
return train, test
# 计算物品之间的相似度
def ItemSimilarityBest(self):
print("计算物品之间的相似度")
# 已经算完了,直接用
if os.path.exists("data/item_sim.json"):
itemSim = json.load(open("data/item_sim.json", "r"))
else:
# 物品相似度
itemSim = dict()
# 用户对每个不同电影的评分看作一次行为
# 计算行为次数
item_user_count = dict()
# 物品的共现矩阵
count = dict()
# 遍历训练数据集
# 获取共现矩阵
# 共现矩阵每个元素表示同时喜欢两个物品的用户数
# 是实对称稀疏矩阵
for user, item in self.trainData.items():
# 遍历当前用户所评分过的所有电影
for i in item.keys():
# 进行记录
item_user_count.setdefault(i, 0)
# 用户进行过评分
if self.trainData[str(user)][i] > 0.0:
# 记录行为次数
item_user_count[i] += 1
for j in item.keys():
count.setdefault(i, {}).setdefault(j, 0)
# 同时对两个电影进行了评分
if self.trainData[str(user)][i] > 0.0 and self.trainData[str(user)][j] > 0.0 and i != j:
count[i][j] += 1
# 共现矩阵 -> 相似度矩阵
# 遍历共现矩阵
for i, related_items in count.items():
itemSim.setdefault(i, dict())
for j, cuv in related_items.items():
itemSim[i].setdefault(j, 0)
# 电影i,j之间的相似性
# 是同时对电影i,j进行了评分的行为
# 除以各自的行为乘积再开根号
# 可以抑制热门商品的曝光程度
itemSim[i][j] = cuv / math.sqrt(item_user_count[i] * item_user_count[j])
# 变为json格式
json.dump(itemSim, open('data/item_sim.json', 'w'))
return itemSim
# 为用户进行推荐
def recommend(self, user, k=8, nitems=40):
# 为user进行推荐
# k是和用户每部喜欢的电影最相似的电影数
# nitems是推荐的电影数
result = dict()
# 获取当前用户进行过评分的电影和相应评分
u_items = self.trainData.get(user, {})
# i是评分过的电影
# pi是当前用户对其的评分
for i, pi in u_items.items():
# 从相似矩阵中获取k个和当前电影i最相似的电影和对应的相似值
for j, wj in sorted(self.items_sim[i].items(), key=lambda x: x[1], reverse=True)[0:k]:
# 如果用户已经喜欢这部电影了
# 不算,重新推荐
if j in u_items:
continue
# 加入到推荐结果中
result.setdefault(j, 0)
result[j] += pi * wj
return dict(sorted(result.items(), key=lambda x: x[1], reverse=True)[0:nitems])
二 矩阵分解方法
2.1 论文
(
矩阵分解推荐方法是为了克服协同过滤方法头部效应过于明显(爆款的商品倾向于被更多的推荐给用户,这样普通的商品就缺少曝光机会,缺少公平性),泛化能力较弱而提出的,在2006年Netflix(美国的一个看电影的应用)举办的推荐算法大赛中受到了关注。
矩阵分解推荐方法通过分解用户-物品的交互矩阵,得到用户和物品的隐向量表示,隐向量保存了用户和物品的特征信息[已经有了深度学习中嵌入表示的意思了],利用用户隐向量和物品隐向量的内积衡量用户对物品的喜爱程度,进行推荐。
)
文章题目:《Matrix Factorization Techniques For Recommender Systems》2009 Computer
文章地址:Matrix Factorization Techniques For Recommender Systems
(是一个报告PPT)
以前的协同过滤方法是通过计算与当前用户最相似的用户,然后推荐相应物品,其利用的是用户-物品的交互矩阵
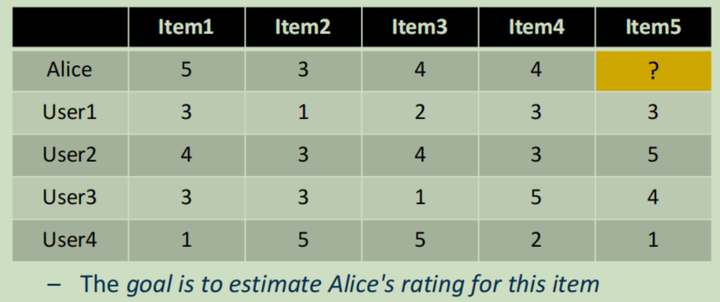
它隐含的假设是过去有相同兴趣的用户,未来也会有相同的兴趣。
可以利用皮尔逊相关系数(pearson correlation)衡量用户之间的相似性

其中 是用户a对于物品p的评分,
是用户a的平均物品评分。
上面的协同过滤是从用户的角度出发的,还可以从物品的角度出发,计算物品之间的相似性,然后推荐和用户喜欢的物品最相似的物品。
本文提出的方法是利用一个隐向量(latent factor)表示用户和物品,然后推荐给用户那些与它隐向量有较大相似性的物品隐向量所对应的物品。

具体的方法流程

- 首先计算出用户和物品的隐向量
- 计算用户和物品隐向量内积
- 推荐给用户内积值比较高的物品
那么如何得到用户和物品的隐向量,可以通过分解用户-物品的交互矩阵或者通过梯度下降进行学习。
通过奇异值分解(SVD)方法对交互矩阵进行分解

通过梯度下降进行学习,损失函数为
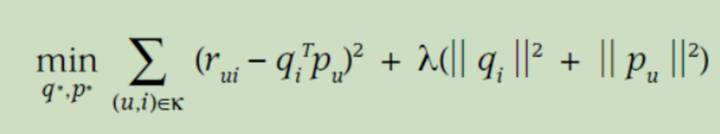
2.2 代码
import pickle
import random
from math import exp
import numpy as np
import pandas as pd
class MF:
# 模型初始化
def __init__(self):
# 用户、物品隐向量的维度
self.class_count = 5
# 训练次数
self.iter_count = 5
# 学习率
self.lr = 0.02
# 正则化系数
self.lam = 0.01
# 获取评分矩阵的分解矩阵p,q
self._init_model()
# 初始化
# 随机生成评分矩阵的分解矩阵p,q
def _init_model(self):
# 评分数据集路径
file_path = 'data/ratings.csv'
# 用户对所有电影的行为集合
pos_neg_path = 'data/lfm_items.dict'
# 读取评分
self.uiscores = pd.read_csv(file_path)
# 获取所有的用户ID
self.user_ids = set(self.uiscores['UserID'].values)
# 获取所有电影ID
self.item_ids = set(self.uiscores['MovieID'].values)
# 加载用户互动电影集合
self.items_dict = pickle.load(open(pos_neg_path, 'rb'))
# 先随机生成评分矩阵的分解矩阵
# 后面通过训练过程调整
array_p = np.random.randn(len(self.user_ids), self.class_count)
array_q = np.random.randn(len(self.item_ids), self.class_count)
# 转换为DataFrame格式
self.p = pd.DataFrame(array_p, columns=range(0, self.class_count), index=list(self.user_ids))
self.q = pd.DataFrame(array_q, columns=range(0, self.class_count), index=list(self.item_ids))
# 计算用户 user_id 对 item_id的感兴趣程度
def _predict(self, user_id, item_id):
# Pandas 的ix()函数会先以loc()获取指定索引的值
# 如果没获取到会继续尝试以iloc()获取
# 已经不推荐使用
# 这里可以改成loc[user_id]
# mat转换为矩阵
# 因为p,q要相乘
# 注意q进行了转置 .T
p = np.mat(self.p.ix[user_id].values)
q = np.mat(self.q.ix[item_id].values).T
r = (p * q).sum()
# 借助sigmoid函数,转化为是否感兴趣的概率
logit = 1.0 / (1 + exp(-r))
return logit
# 损失函数
def _loss(self, user_id, item_id, y, step):
e = pow((y - self._predict(user_id, item_id)), 2) / len(y)
print('Step: {}, user_id: {}, item_id: {}, y: {}, loss: {}'.format(step, user_id, item_id, y, e))
return e
# 带正则化的梯度下降
def _optimize(self, user_id, item_id, e):
# 梯度
gradient_p = -e * self.q.ix[item_id].values
# 正则化项
l2_p = self.lam * self.p.ix[user_id].values
# 梯度下降p更新的部分
delta_p = self.lr * (gradient_p + l2_p)
# q
# 同理
gradient_q = -e * self.p.ix[user_id].values
l2_q = self.lam * self.q.ix[item_id].values
delta_q = self.lr * (gradient_q + l2_q)
# 梯度下降更新
self.p.loc[user_id] -= delta_p
self.q.loc[item_id] -= delta_q
# 训练模型
def train(self):
for step in range(0, self.iter_count):
# 获取用户进行过评分和没进行过评分的电影集合
for user_id, item_dict in self.items_dict.items():
print('Step: {}, user_id: {}'.format(step, user_id))
# 获取集合中的每一个电影
item_ids = list(item_dict.keys())
random.shuffle(item_ids)
# 计算损失,进行更新
for item_id in item_ids:
# item_dict[item_id]是真实的评分标签
# 与模型的预测值计算损失
e = self._loss(user_id, item_id, item_dict[item_id], step)
self._optimize(user_id, item_id, e)
# 降低学习率
self.lr *= 0.9
# 保存模型
self.save()
# 保存模型
def save(self):
f = open('data/lfm.model', 'wb')
pickle.dump((self.p, self.q), f)
f.close()
(下面的代码需要懂一点PyTorch+Scilit-learn)
三 因子分解机方法
3.1 论文
(
了解因子分解机之前需要先了解一下基于逻辑回归的推荐方法。
前面说的协同过滤和矩阵分解仅利用了用户和物品的交互矩阵信息,没有有效利用用户、物品其它有效的特征。逻辑回归方法综合考虑用户,物品不同的特征,生成更加全面的推荐结果。逻辑回归赋予每个不同的特征以不同的权重,将推荐问题转换为用户对物品产生‘正反馈’行为的分类问题,比如点击率(Click Through Rate,CTR)预估问题。
逻辑回归表达式为
其中X是输入的各种特征,W是模型需要通过训练而学习得到的权重,sigmoid()是
因子分解机认为逻辑回归模型表达能力不强,会造成有效信息的丢失,引入了特征交叉的概念。逻辑回归只是给不同特征以不同权重,没有考虑不同特征之间的组合,特征交叉指的就是不同特征之间的组合。
)
3.1.1 FM(Factorization Machines)
论文题目:《Factorization Machines》2010 IEEE International Conference on Data Mining
受SVM思想的启发,我们提出了一种新的分类模型-因子分解机(FM),但是有别于SVM,在FM中我们引入了特征交叉的概念,使模型可以学习出不同特征之间的组合信息。
SVM在推荐系统中效果不好的一个原因是它无法在核空间中处理过于稀疏的数据。FM可以用来处理大规模稀疏数据。
一个二阶FM的表达式为
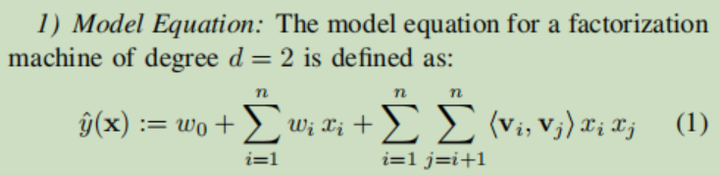
模型要通过训练学习得到的参数有
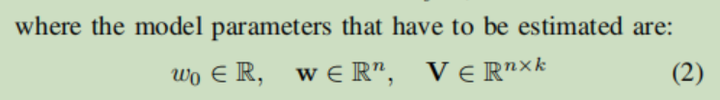
表示内积
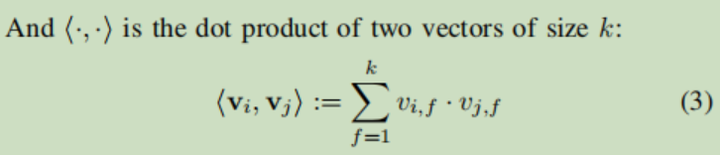
k是我们设置的一个超参数,代表因子(V)的维度。
一个二阶的因子分解机能够捕获不同特征 单独的重要程度 和 成对特征组合的重要程度

(什么意思呢,FM相当于为每一个特征学习出来一个特征表示向量 ,向量内积的结果作为这对特征组合的权重,其中特征交叉这项
还有一个叫法是‘双线性’)
3.1.2 FFM(Field-aware Factorization Machines)
论文题目:《Field-aware Factorization Machines for CTR Prediction》2016 RecSys
论文地址:《Field-aware Factorization Machines for CTR Prediction》
以往的CTR预估问题一般用逻辑回归模型进行求解,其损失函数为
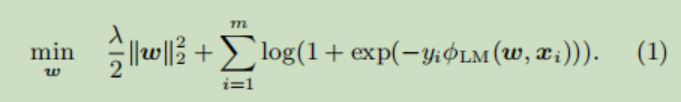
但是逻辑回归无法捕获不同特征之间的交叉信息,后来的Poly2,FM模型引入特征交叉解决了这个问题。
在FM的基础上,FFM再为每个特征引入域的概念,增强模型的泛化性,让模型能够学习出更多的信息
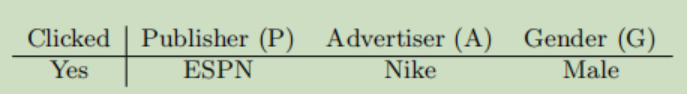
ESPN...那行是特征,上面的P,A...是特征所属的域
对于上面这些特征,FM特征交叉的权重计算方式为
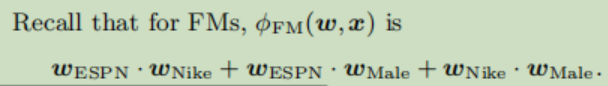
但是在FFM中计算方式为

(注意对比这俩的区别,因为引入了特征域的概念,即使是同一个特征,在不同域中也具有不同的表示,所以 是两个不同的隐向量。剩下的和FM相同,没有变化)
FFM特征交叉部分的计算公式为
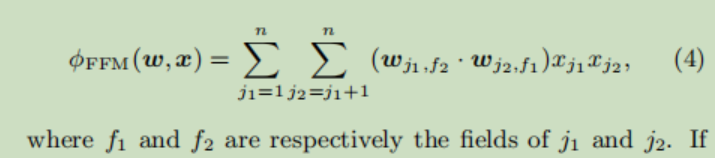
3.2 代码
class FM(nn.Module):
def __init__(self, dim, k):
super(FM, self).__init__()
# 特征维度
self.dim = dim
# 特征隐向量维度
self.k = k
# FM的一阶部分,公式的前两项
self.w = nn.Linear(self.dim, 1, bias=True)
# 初始化V矩阵
self.v = nn.Parameter(torch.rand(self.dim, self.k) / 100)
# 前向传递,建立计算图
def forward(self, x):
# 输入的X是特征矩阵
# 维度[batch_size,dim]
# 先计算公式的线性部分
linear = self.w(x)
# 计算二阶特征交叉部分
# 用的是论文中的化简公式
quadradic = 0.5 * torch.sum(torch.pow(torch.mm(x, self.v), 2) - torch.mm(torch.pow(x, 2), torch.pow(self.v, 2)))
# 转换为概率
return torch.sigmoid(linear + quadradic)四 多模型融合方法
4.1 论文
(前面的FM,FFM虽然引入了不同特征之间的组合,但是也只是停留在二阶特征交叉(二个特征)的程度,如何向推荐模型中引入不同阶的特征交叉呢,这就是下面这些方法要解决的问题,而且这些模型已经有了端到端训练的想法,是传统推荐方法到深度学习推荐方法的过渡)
4.1.1 GBDT+LR
论文题目:《Practical Lessons from Predicting Clicks on Ads at Facebook》2014 KDD
论文地址:《Practical Lessons from Predicting Clicks on Ads at Facebook》
方法没啥好说的,就是用GBDT进行特征组合和提取,然后将得到的结果输入到逻辑回归模型中,进行CTR预测。但是这种特征工程模型化的想法具有重要的意义。
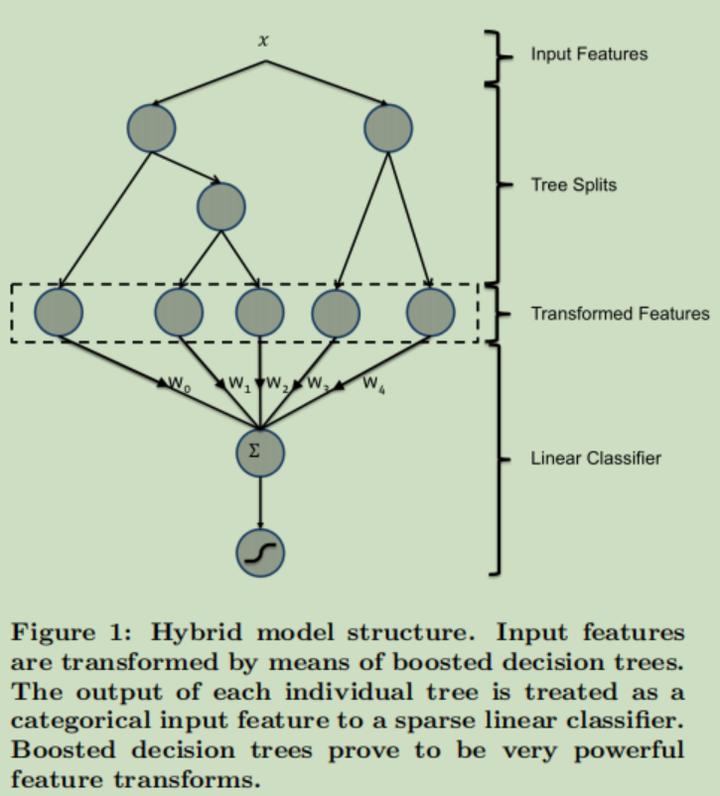
4.1.2 LS-PLM
论文题目:《Learning Piece-wise Linear Models from Large Scale Data for Ad Click Prediction》2017
论文地址:《Learning Piece-wise Linear Models from Large Scale Data for Ad Click Prediction》
这个是Alibaba提出的一个具有影响力的推荐模型。

首先对输入特征的特征空间进行划分 ,然后在每个划分出来的特征空间中进行预测
,最后利用
将预测结果转换为概率。
具体应用时是
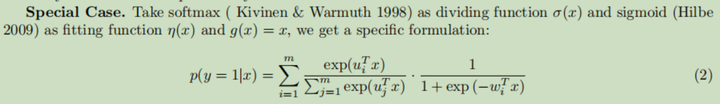
训练损失函数为
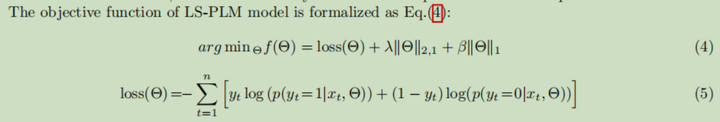
4.2 代码
# coding=UTF-8
import pandas as pd
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
class GBDTAndLR:
def __init__(self):
# 训练数据集路径
self.file = "data/new_churn.csv"
# 获取数据
self.data = self.load_data()
# 拆分数据
self.train, self.test = self.split()
# 加载数据
def load_data(self):
return pd.read_csv(self.file)
# 拆分数据集
def split(self):
# train:test = 9:1 拆分
train, test = train_test_split(self.data, test_size=0.1, random_state=40)
return train, test
# 模型训练
def train_model(self):
# 获取特征和标签
lable = "Churn"
ID = "customerID"
x_columns = [x for x in self.train.columns if x not in [lable, ID]]
x_train = self.data[x_columns]
y_train = self.data[lable]
# 创建gbdt模型,并训练
gbdt = GradientBoostingClassifier()
gbdt.fit(x_train, y_train)
# 创建lr模型,并训练
lr = LogisticRegression()
lr.fit(x_train, y_train)
# 模型融合
# 就是把GBDT的输出作为LR的输入
gbdt_lr = LogisticRegression()
# one-hot编码
enc = OneHotEncoder()
# 100是迭代次数,调整维度
# 先对输入数据进行one-hot编码
# 然后输入到GBDT进行特征提取
# 然后将GBDT的输出作为LR的输入
enc.fit(gbdt.apply(x_train).reshape(-1, 100))
gbdt_lr.fit(enc.transform(gbdt.apply(x_train).reshape(-1, 100)), y_train)
return enc, gbdt, lr, gbdt_lr
基于深度学习的推荐方法可以看我的
内容中包含的图片若涉及版权问题,请及时与我们联系删除




评论
沙发等你来抢