计算机图形学感觉都是在搞一些很肤浅的东西 -- 如果你觉得计算机图形学肤浅, 可能是因为你还没有意识到在计算机上重现大自然有多复杂.
计算机图形学是一门对个人的综合素质要求比较高的学科.视乎研究的具体方向不同, 需要研究者有很好的编程功力(独立完成项目), 很好的数学功底: 几何, 微分几何, 偏微分方程, 常微分方程, 概率论和统计学(machine learning), 数值方法, 物理学(声,光,材料力学, 流体力学, 热学....), 还有心理学, 良好的文学以及艺术修养.
虽然计算机图形学的"研究成果"大多都是用在娱乐业上, 但是计算机图形学的"研究过程", 堪比任何一门听起来更高大上的学科. 我为什么敢这样说呢? 因为我有例子.
例子1: 计算机图形学对于现实世界光学的真实再现.(physically based rendering)

为了真实地在计算机上再现人肉眼看到的东西, 人们必须去理解光与几何的作用过程, 并通过程序把它计算出来. 现实世界的光学比我们所理解得还要复杂, 于是乎, 我们需要研究和学习:
采样理论:
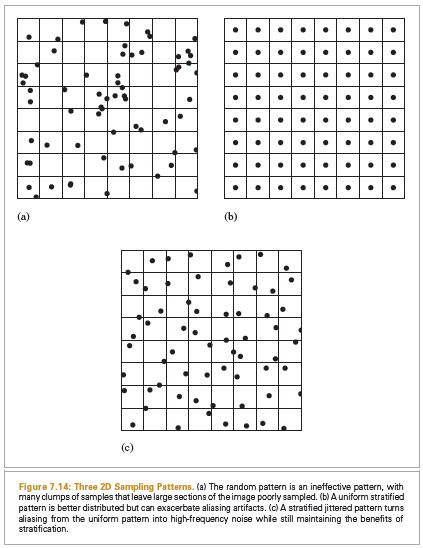

数值积分:
各种光照模型:

Bidirectional reflectance distribution function




等,
想要真实地再现一个物理场景, 计算机图形学的研究者需要去学习和研究真实的物理光学的模型, 并把将这些过程编成计算机程序, 从而让计算机能够去计算出结果和图像.
所以在这一点上, 计算机图形学, 也是物理(光学)模型的一个试金石. 对还是不对, 渲染出来看一看. 骗得过人眼吗?
例子2 : 计算机图形学, 研究人对于图案的意识过程, 并让计算机由产生更好的design.
比如从二维手绘自动生成三维模型(
True2Form: 3D Curve Networks from 2D Sketches via Selective Regularization
):
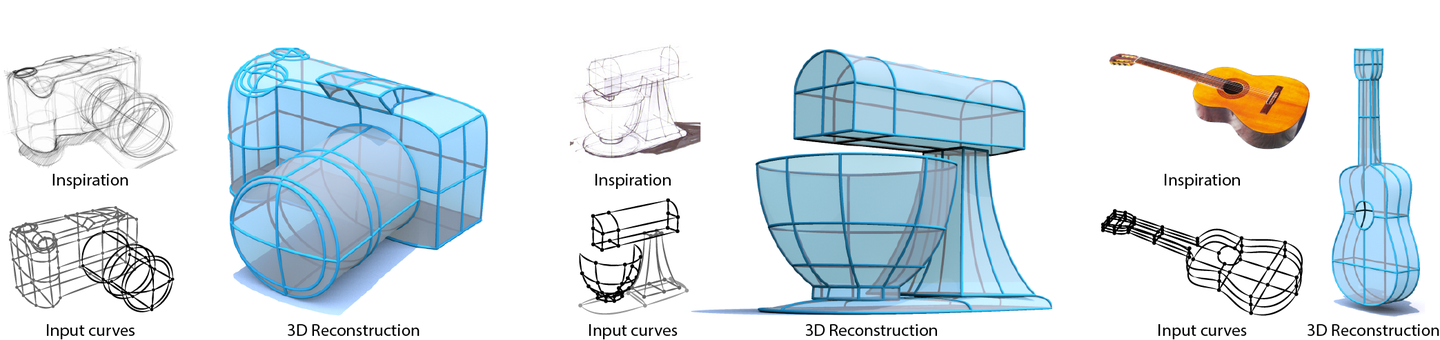
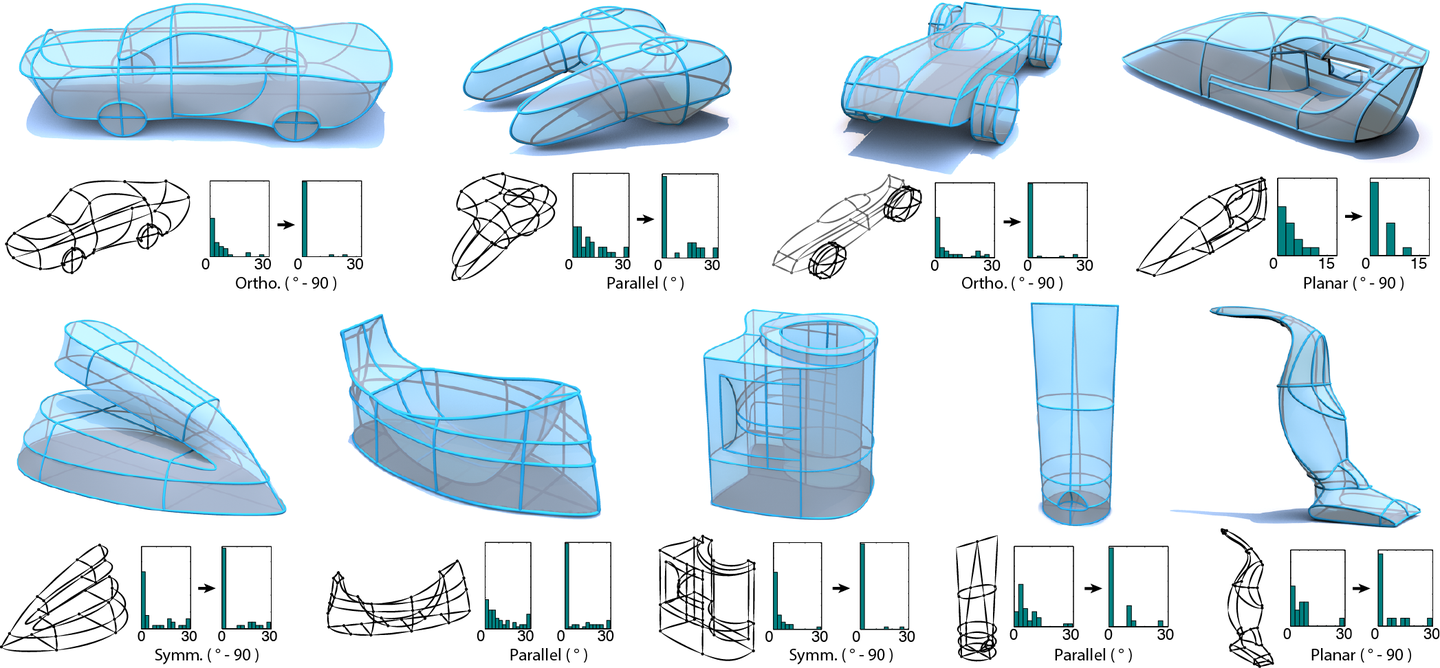
例子3: 计算图形学研究艺术的思维, 并尝试让计算机来生成风格化的艺术:
Stylizing Animation By Example

http://graphics.pixar.com/library/ByExampleStylization/mainVideo.mov
例子4:
计算机图形学, 研究基础的几何计算问题, 并让与之相关的工程数值计算领域收益
Tetrahedral Mesh Generation by Delaunay Refinement
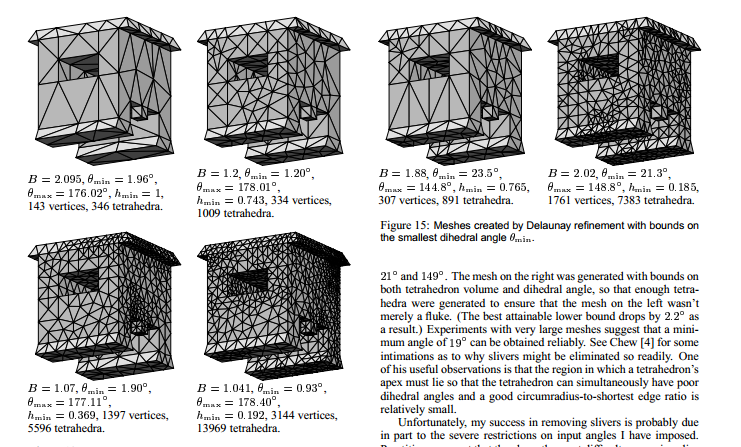
例子5:
计算机图形学, 研究基础的数值数学与物理, 从而允许计算机通过计算来重现真实:

Walt Disney Animation Studios
Adaptive Tearing and Cracking of Thin Sheets
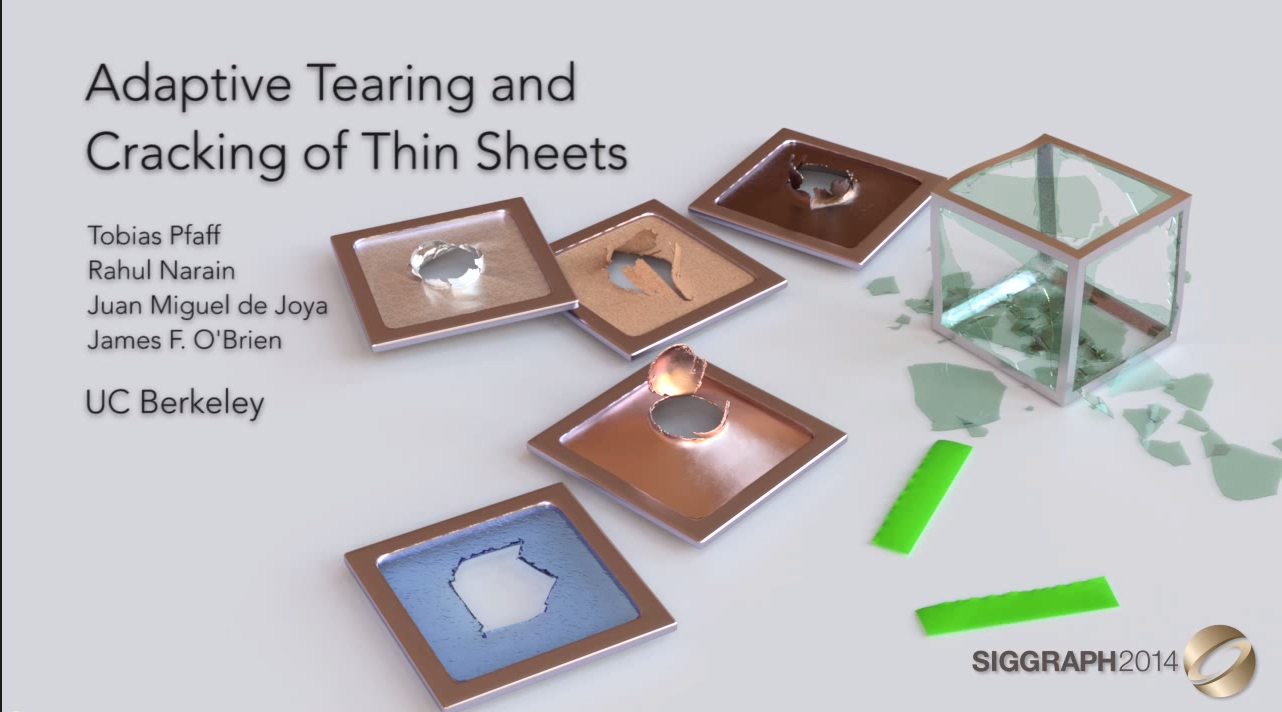
http://graphics.berkeley.edu/papers/Pfaff-ATC-2014-07/adaptiveCracks.mp4
Detailed Water with Coarse Grids Combining Surface Meshes and
Adaptive Discontinuous Galerkin
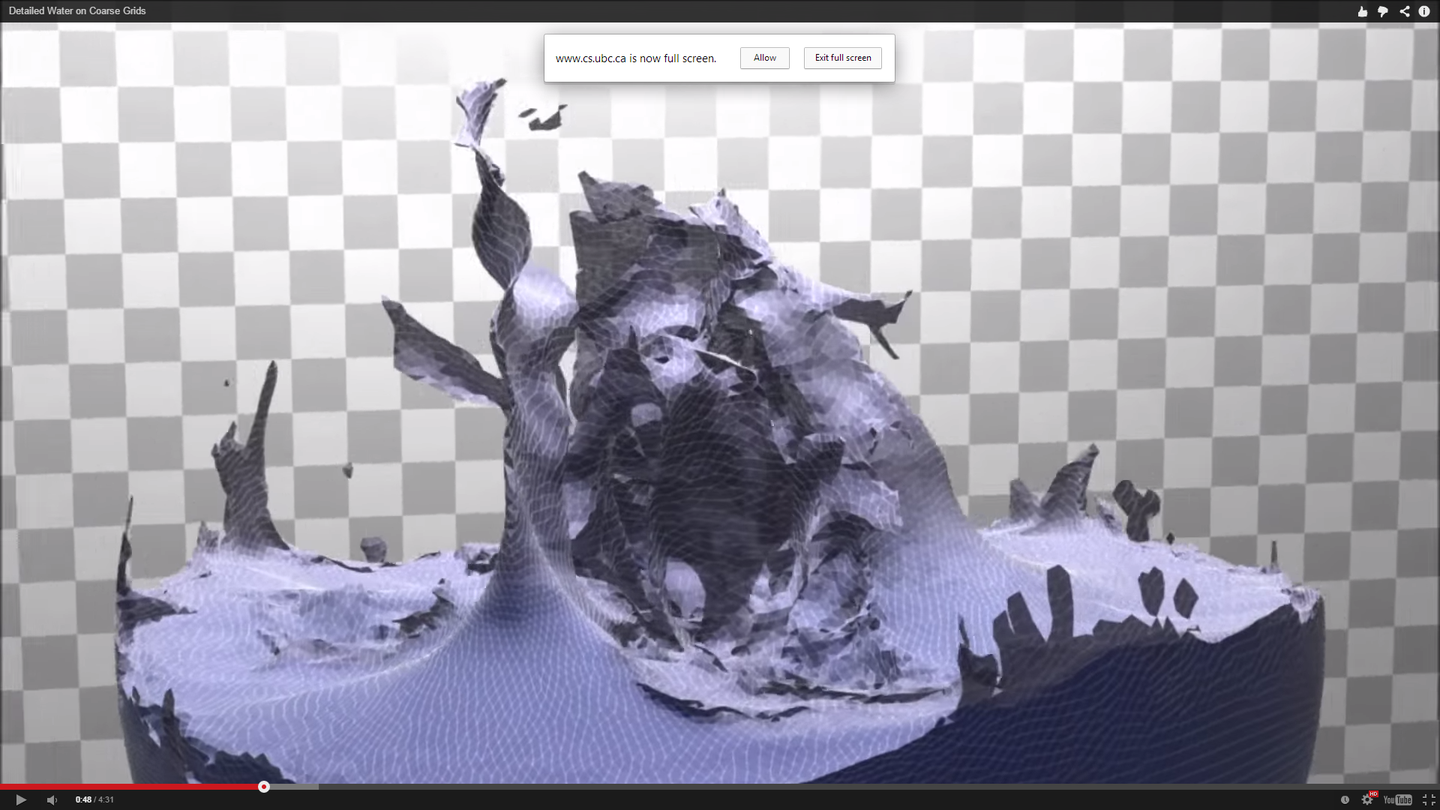
and many more:
例子6: 计算机图形学甚至研究声音的形成, 并利用物理输入再现它:
Toward High-Quality Modal Contact Soundhttp://www.cs.cornell.edu/projects/Sound/mc/ModalContactSound2011_high.mov
例子7: 计算机图形学, 研究人体和动物的肌肉运动力学, 并试图在计算机上重现真实的运动:
http://www.cs.ubc.ca/~van/papers/2013-TOG-MuscleBasedBipeds/index.html
http://vimeo.com/79098420
我所说的这些东西, 还只是计算机图形学所有研究内容的冰山一角...放在这个答案里只做一个抛砖引玉的作用...CG的研究范围很广, 研究内容很多, 你可以说它明明是物理,人工智能,数值数学等的研究范围了,这是因为现在的图形学研究,随着不断增长的电影工业和研究者本人的兴趣不同,早已超越了图形学本身,延伸进了科学研究的各个方面. 图形学的研究, 同时也加深了我们对物理世界甚至人类自身的理解, 发展着计算方法的同时,也验证着我们已有的物理模型.
说了这么多关于CG的, 我觉得有必要提一些关于machine learning的:
(看题主这么热情,我一句不说也不好).
我对machine learning了解得不是很多, 只能说一些在数值方法角度讲它与CG学的研究的共通之处:
突优化问题的求解需要大量的高维线性方程组求逆算法, 大规模并行,代数多尺度网格,preconditioning, 稀疏矩阵,gradient descent…其中的很多数学与cg的物理模拟算法中的数学都是相通的.
machine learning面对的问题维度更高, 对高维度的对象做积分时,我们一样使用monte carlo 数值积分算法来加快积分求解速度.
这种课题背景不同,实质理论却想通的现象是现代应用科学中的本质现象, 题主问出这样的问题,可能部分也是因为对本质之不查?
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢