OpenAI为Lean语言(2013年由微软研究院的Leonardo de Moura发起)建立了一个神经定理验证器,可以学习解决各种具有挑战性的高中奥林匹克竞赛问题,包括来自AMC12和AIME竞赛的问题,以及两个改编自IMO的问题(相关论文)。
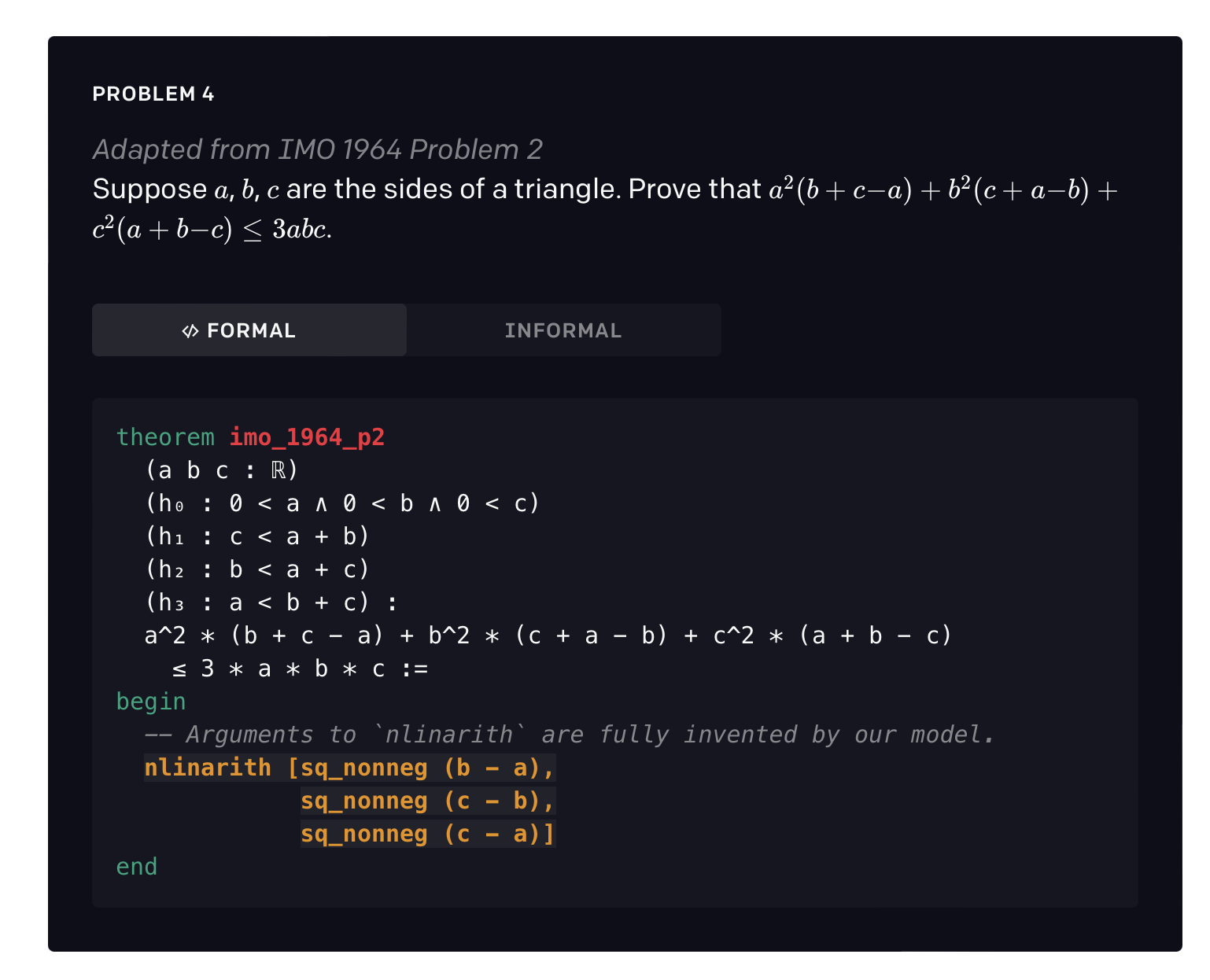
验证器使用一个语言模型来寻找形式化语句的证明。每次找到一个新的证明,就把它作为新的训练数据,从而改进神经网络,使它能够迭代地找到越来越难的语句的解决方案。模型在miniF2F基准上取得了新的SOTA(41.2% vs 29.3%)——这是一个具有挑战性的高中奥林匹克问题集合。
形式数学涉及两个主要挑战,使得简单的强化学习应用不太可能成功。
- 无限的行动空间:形式数学不仅有一个极其庞大的搜索空间(例如围棋),它还有一个无限的行动空间。在证明搜索的每一步,模型必须不是从行为良好的有限行动集合中选择,而是从复杂和无限的战术集合中选择,涉及到必须生成的外生数学术语(例如,生成一个用作见证的数学语句,一个用于 "存在一个x s.t. ... "等步骤的对象,或者一个切割,在证明的中间引入和连锁一个勒姆)。
- 缺乏自我游戏:与2人游戏相反,证明者不是与对手游戏,而是与一组要证明的语句游戏。当面对一个太难的语句时,没有明显的重构可以让验证者产生中间的更容易的语句来首先解决。这种不对称性阻止了对2人游戏成功的自我发挥算法的应用。
通过在搜索证明时从语言模型中抽取行动来解决无限行动空间的问题。语言模型有能力生成战术调用以及经常需要作为论据的原始数学术语。解决缺乏自我游戏的基础是观察到2人游戏中自我游戏的关键作用是提供一个无监督的课程。我们的方法建议用一套难度不同的问题陈述(不需要证明)来取代这种无监督的课程。经验表明,当这些辅助问题的难度足够大时,训练程序能够解决越来越难的问题的课程,最终普及到关心的问题集。
虽然这些结果非常令人兴奋,证明了深度学习模型在与正式系统互动时能够进行非微妙的数学推理,但离最佳学生表现仍然非常遥远,只能偶尔而非持续地关解决有挑战性的奥林匹克竞赛问题。尽管如此,OpenAI希望其工作将激励这一领域的研究,特别是对IMO大挑战的研究,其提出的声明课程学习方法将有助于加速自动推理的普遍进展。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢