- 论文链接:https://arxiv.org/abs/2112.04148
- Git代码:https://github.com/WanquanF/NeuralPoints
摘要
本文介绍来自中国科学技术大学的一篇CVPR 2022工作:Neural Points,该工作通过神经隐式场对点云局部区域进行建模,并通过聚合得到点云全局的连续隐式表示。传统点云一般将每个点看做3D空间中的一个离散采样点,因此,只有连续稠密的点云数据才能具有较好的3D表达能力,即点云的表达能力与其分辨率成正比关系。为了解决这一问题,点云上采样任务被提出以提升离散点云的分布稠密度。然而,现有上采样方法仍将每个点视为离散采样数据点,并未从本质上解决这一问题。本文提出Neural Points,其中每个点通过神经场表示一个局部连续的几何形状。因此,Neural Points可以表达更复杂的几何形状,具有更强的表达能力。实验结果表明,Neural Points具有较强的表达能力,具有较好的鲁棒性和泛化能力,它比最先进的点云上采样方法有很大的优势。
贡献
与传统的表示方法不同的是,Neural Points的每个点编码一个通过神经场表示的局部点云平面。具体来说,每个点的表面贴片被表示为2D参数域和3D局部超平面之间的局部同构,并通过神经场隐式表示该同构。由于其连续的性质,Neural Points不受分辨率的限制,对复杂几何形状具有强大表示能力。同时,Neural Points的训练模型对所有局部点云都是共享的,因此其存储开销很小。
在本文之前,已有一些研究通过单个神经场来表示整个表面模型,它们均使用局部点特征构建神经场。而在本文提出的Neural Points具有更好的提取细节的能力、较强的泛化能力和较低的训练数据需求。具体来说,基于三维局部块与二维流形都是二维链接域的同构基(原文:3D local patch on the 2D manifold is isomorphic to a 2D simply connected disk),Neural Points利用局部神经场构造二维参数域和三维局部超平面之间的连续映射。在神经场的作用下,每个三维局部超平面可以被看作是一个定义在二维参数域内的参数曲面。为此,Neural Points采用编码器提取逐点局部特征,并将局部特征作为传递到神经场网络的一部分。利用局部形状信息,Neural Points可以很好地表示表面超平面,训练后的网络模型共享于所有3D平面。最后,本文设计了一种整合策略以将所有的局部神经域整合在一起,形成最终的全局形状。神经点模型采用具有丰富几何细节的高分辨率几何曲面进行训练,使训练后的神经点模型既能表示低频几何结构,又能表示高频几何细节。
总的来说,本文贡献点如下:
- 提出了一种新的点云表示方法-Neural Points,其表示能力大大超过传统的点云表示,并具有低存储开销;
- 利用神经隐函数和深度局部特征来表示局部神经场,并设计了一种集成策略来形成最终的全局形状;
- 实验结果表明,Neural Points对各种输入具有良好的鲁棒性和泛化能力,对点云上采样任务的应用比现有方法有更好的性能。
方法
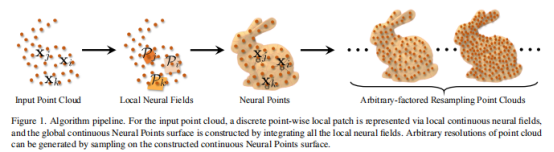
Neural Points的算法流程如上图所示主要包括三个步骤,1) 给定输入点云,首先为每个局部点云块构建局部神经隐式场;2) 将局部神经场聚合在一起形成全局形状;3) 通过全局神经场重采样任意数量的点。
步骤一:构建局部神经隐式场
假设输入点云X包含I个点x,则可以x为中心将所有点构成的曲面划分为重叠的局部块P。每个三维局部块P同构于一个二维的参数域D,即可以在它们之间构造一个双射映射:
![]()
其中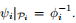 。
。
构建局部神经隐式场的步骤如下图所示:
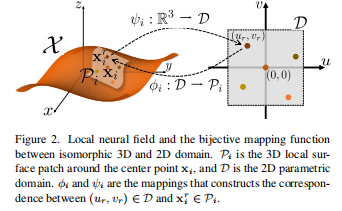
给定任意二维采样点(ur,vr)∈D , 可以计算映射函数ψ作为其对应的3D采样点。类似地, 对于任何3D点 x∈P, 可以计算其对应的 2D 坐标(ur,vr)∈D。
步骤二:将局部神经场聚合在一起形成全局形状
这一步骤主要通过下式完成:
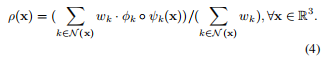
其中x为任意三维点,wk的计算依赖于x到各个小块的距离。法向量也可以类似计算,这样就获得了全局连续隐式。
步骤三:通过全局神经场重采样任意数量的点
这一步骤通过在二维参数域D中均匀地采样, 并将二维采样点映射到三维局部块上。具体来说, 对于在每个中心点X的附近采样 , 然后将它们映射到 3D超平面。之后, 从所有小块采样点的并集中进行均匀采样以获得所需的结果。
实验
本文在Sketchfab数据集上对模型进行训练和测试,该数据集包含90个训练模型和13个具有丰富几何特征的测试模型,使用相同的数据集训练所有的比较方法以进行公平比较。
本文首先给出了点云上采样任务的指标对比:
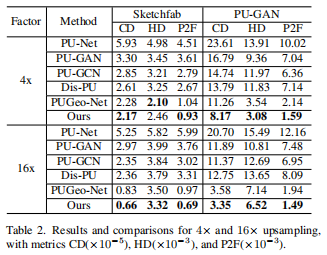
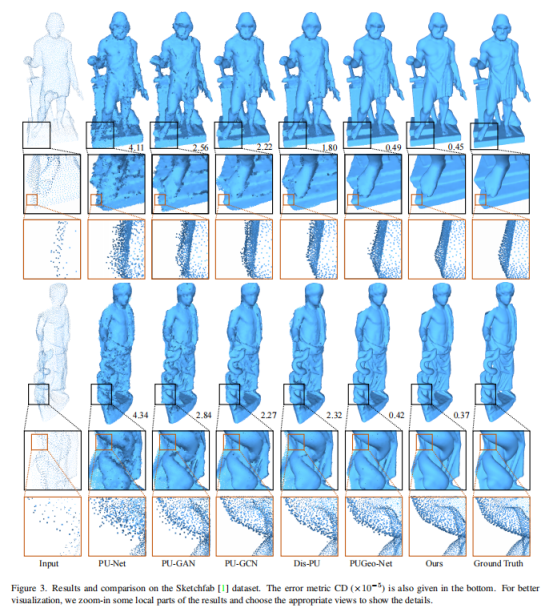
可以看到,Neural Points在指标上取得了最好的性能。而在下图展示的视觉对比中,Neural Points同样取得了SOTA的性能。PU-Net的结果总体上是混乱的。PU-GAN比PU- Net性能较好,但也会产生一些异常值。PU-GCN的性能优于上述两种方法,可以保持平坦区域,但在特征丰富的区域仍会产生一些噪声点。
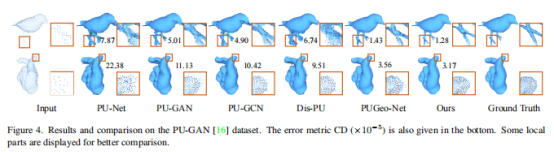
本文还展示了一些未经训练直接泛化到PU-GAN数据集的结果:
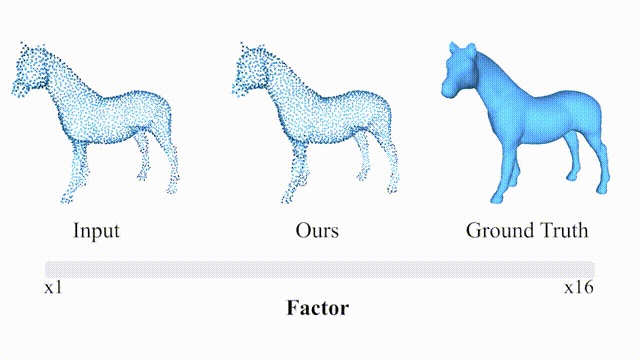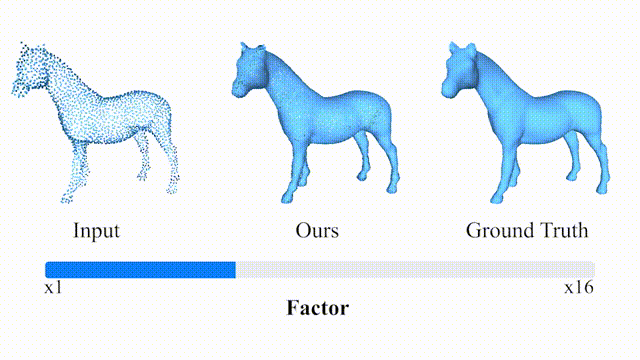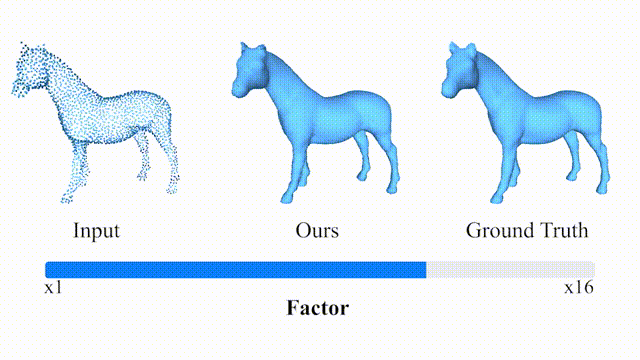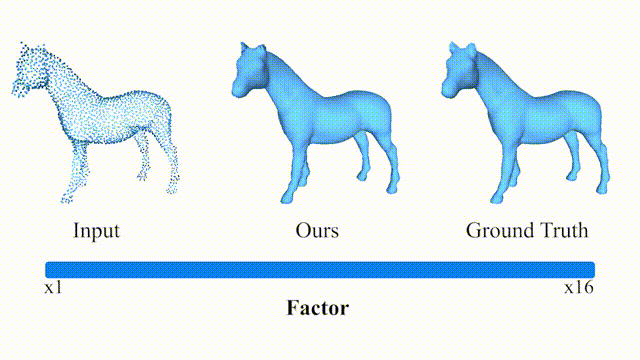
在大采样因子下以及真实数据上的结果:

内容中包含的图片若涉及版权问题,请及时与我们联系删除




评论
沙发等你来抢