2022年1月，智源研究院发布新一版《白皮书：人工智能的认知神经基础》[1]。其中介绍了很多认知神经与人工智能交叉前沿方向的成果。今天我们就来讲讲其中一个概念——神经流形。

知识点

1.神经流形被用于描述大脑中神经元的群体活动。大脑将外部信息编码为高维神经活动空间内的低维流形。

2.研究神经流形，可以实现对具体认知能力的编码，并进一步分析神经网络中处理信息的方式，有助于理解神经网络和人类大脑认知功能的模式和规律。

定义

流形的概念来自几何学。在拓扑学中，被定义为一个局部近似欧式空间的拓扑空间，在微分几何中，在拓扑空间的基础上，流形的定义增加了平滑的属性，要求其可微。流形可以被想象成若干个局部欧式空间覆盖在相同维度的全局空间上。[1]

近年来，流形被越来越多地用于描述大脑中神经元的群体活动[2]。例如，可以把神经元的群体活动状态描述成一个向量，该向量中的每一个分量，代表一个神经元的活动[3]。可以想象一个高维坐标系，一个向量代表一个点。在高维状态空间中，每一个轴代表一个神经元放点活动。如果有N个神经元参与该刺激的编码，对应坐标系就代表了一个N维的神经活动空间（Neural Response Space）。

近年来，神经科学家提出了一个通用的流形假说：大脑将外部信息编码为高维神经活动空间内的低维流形。[1]

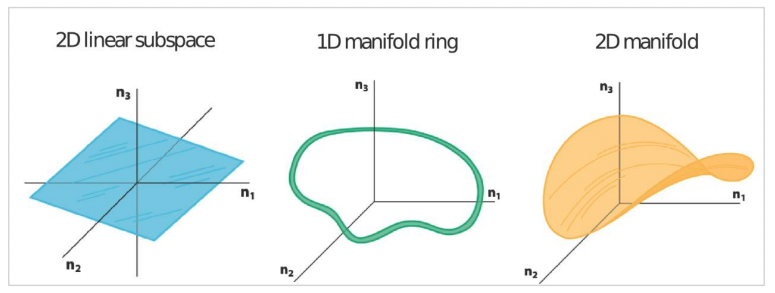
图注：三维空间中的1维、2维流形示例。[7]

研究神经流形对人工智能研究的作用

1.通过神经流形，实现对具体认知能力的编码

例如，大脑中的网格细胞能够表征环境空间，网格细胞也有对应的流形[4]，因此可以通过对网格细胞流形的变化，研究大脑在环境空间变化时，其认知能力的变化。Derdikmen等人提出空间以类似马赛克的形式被神经元编码的假说。[5]

每一个子空间（马赛克）作为一个环境单位被相应的流形所表征。在实验中，研究者先训练大鼠熟悉一个方形环境，神经元的网格状放电形态随即出现，在环境中放入障碍物，将原先的环境被分割成若干区域后，神经元的放电形态也发生变化，形成了特定区域的独特编码。

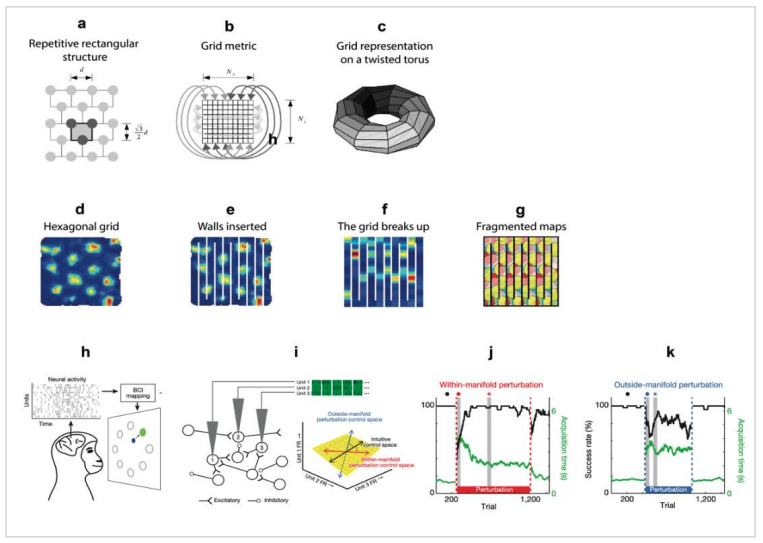
图注：a-c,网格细胞流形表征的概念模型[4];

d-g，网格细胞的规则放电形态随空间 形态变化而变化[5]；

h-k，流形在大脑内存在的神经科学证据[8]。

这说明：神经元能够对复杂环境的每个子空间进行独立编码，并由相应的流形所表征，且流形能够随着环境发生变化。这样，我们可以通过神经流形，实现对具体认知能力的编码。

2.基于神经流形，进一步分析神经网络如何处理信息

例如，在物体识别任务中，外部世界的同一类刺激，对应了神经活动空间内的一个流形，因此大脑的识别功能可以被认为是通过对不同流形在嵌入空间内的分割来实现。Cohen等人基于统计力学，发明了分类容量（Classification Capacity）的量化指标，并探索了神经网络中分类容量和神经流形的维度、半径、和中心位置之间的关联。[6]

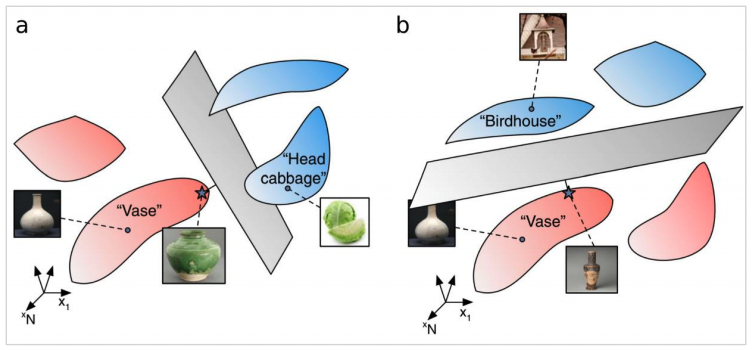
图注：线性分类花瓶流形和白菜流形(a)与花瓶和鸟屋(b)使用了不同的锚点（星号）[6]

研究发现，在完成训练的神经网络中，越接近输出的层中的神经流形维度和半径越低，不同流形的中心相关性越低，而分类容量约稿，因此神经流形的几何特征决定了分类容量。在这些几何特征中，流形维度对分类容量的贡献最大。研究者推测，大脑中的信息处理也可能是通过改变流形的几何特征，使其便于线性分割。

注：本文主要内容来自《白皮书：人工智能的认知神经基础》（2021年），白皮书编写组成员张博、苏杰、蒋龙生等，指导专家为刘嘉、宋森、吴思、方方、余山、陈良怡，点击这里下载原文。

本人在此对白皮书的编写组和指导专家表示感谢。

参考链接

[1] 张博、苏杰、蒋龙生等（2021）白皮书：人工智能的认知神经基础。链接： https://ticket-assets.baai.ac.cn/uploads/2021《人工智能的认知神经基础白皮书》.pdf 

[2] Chung, S., & Abbott, L. F. (2021). Neural population geometry: An approach for understanding biological and artificial neural networks. Current Opinion in Neurobiology, 70, 137–144. https://doi.org/10.1016/j.conb.2021.10.010

[3] Seung, H. S., & Lee, D. D. (2000). The Manifold Ways of Perception. Science, 290(5500), 2268–2269. https://doi.org/10.1126/science.290.5500.2268

[4] Guanella, A., Kiper, D., & Verschure, P. (2007). A model of grid cells based on a twisted torus topology. International journal of neural systems, 17(04), 231-240.

[5] Derdikman, D., & Moser, E. I. (2011). A manifold of spatial maps in the brain. Space, Time and Number in the Brain, 41-57.

[6] Cohen, U., Chung, S., Lee, D. D., & Sompolinsky, H. (2020). Separability and geometry of object manifolds in deep neural networks. Nature Communications, 11(1), 746. https://doi.org/10.1038/s41467-020-14578-5

[7] Vyas, S., Golub, M. D., Sussillo, D., & Shenoy, K. V. (2020). Computation through neural population dynamics. Annual Review of Neuroscience, 43, 249-275.

[8] Sadtler, P. T., Quick, K. M., Golub, M. D., Chase, S. M., Ryu, S. I., Tyler-Kabara, E. C., ... & Batista, A. P. (2014). Neural constraints on learning. Nature, 512(7515), 423-426.

内容中包含的图片若涉及版权问题，请及时与我们联系删除