
论文链接:https://arxiv.org/pdf/2204.04676v1.pdf
代码链接:https://github.com/megvii-research/NAFNet
导读
近来,尽管图像复原领域取得了重大的研究进展,但一流模型的计算复杂度仍呈现出上升趋势,这极大地影响了复原算法的分析和对比。因此,来自旷世研究院的作者们在本文提出了一种简单的基准模型,该模型不仅可以在性能上超越现有SOTA方法,还具有更小的计算量。为了实现基准模型的简化,作者证实对于复原模型来说,Sigmoid,ReLU,GELU,Softmax等非线性激活函数并不是必要的结构,将他们进行替换或消除并不会影响模型性能。因此,本文提出了一种Nonlinear Activation Free Network(NAFNet)。实验表明,NAFNet在多项任务上均取得了最佳性能,例如在图像去模糊任务上,PSNR指标超越SOTA方法0.38dB,达到了33.69dB,且减少了8.4%计算量;在图像去噪数据集SIDD上,取得了40.3dB的PSNR,超过已有方法0.28dB但却减少了一半的计算消耗。
贡献
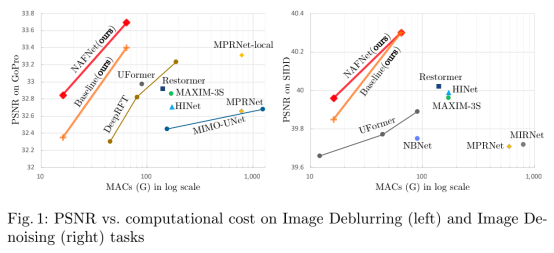
随着深度学习的快速发展,图像复原方法的性能同样取得了显著的推进。尽管如此,这些方法的计算复杂度仍呈现出上升趋势。如下图所示,现有复原方法模块间的计算与越来越多的multi-level特征呈现出相关性。此外,模块内部的计算也不断上升,例如Multi-Dconv Head Transposed Attention Module、Gated Dconv Feed-Forward Network、Swin Transformer Block、HINBlock。这两个现象使得结构设计的验证愈加困难。
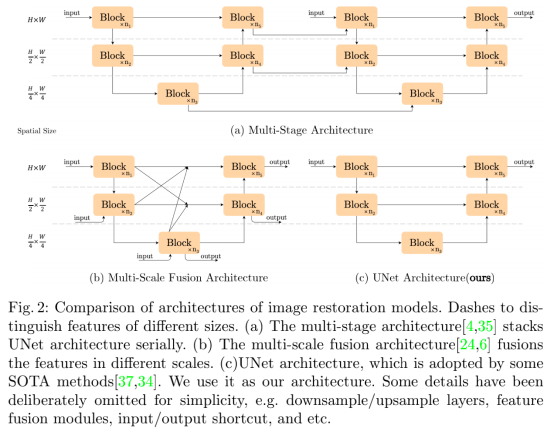
基于上述事实,本文作者提出了一个关键问题:一个具有低模块间、低模块内计算复杂度的深度模型是否也能取得一流的性能?为此,作者采用单阶段的经典模型UNet作为基本架构,并对有卷积、ReLU、残差连接构成的简单模块进行逐元素的验证实验,实验结果证明:Sigmoid,ReLU,GELU,Softmax等非线性激活函数并不是必要的结构,将他们进行替换或消除并不会影响模型性能。
本文的主要贡献可以总结如下:
- 通过分解SOTA方法并提取其基本组成,本文提出了一个具有低复杂性的基准模型,它在性能上超过了以有SOTA方法,并具有较低的计算成本,如图1所示。它可以帮助研究人员激发新的想法,并方便地评估模型架构的选择;
- 揭示了GELU、Channel Attention、Gated Linear Unit之间的联系,通过删除或替换非线性激活函数(如Sigmoid、ReLU和GELU)进一步简化了基准模型,并提出了Nonlinear Activation Free Network,即NAFNet。
- 这是首次证明非线性激活函数在图像复原模型中的非必要性,这项工作可能有潜力扩展计算机视觉方法的设计空间。
方法
基础架构的选择
为构建一个简单的baseline模型,作者选择在基础架构中添加必要且efficient的模块组件。如图2C所示,本文采用单阶段的UNet作为基准架构,并在去噪、去模糊任务上验证了这一做法:
原始模块
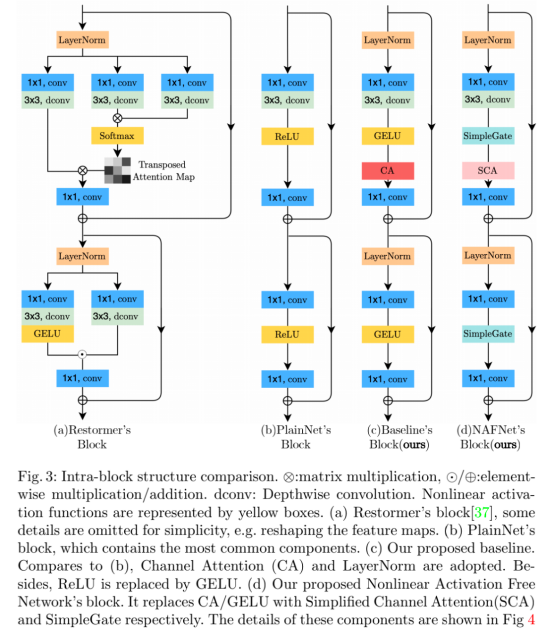
众所周知,深度神经网络是由多个模块堆叠而成。因此,作者接下来研究如何构建神经网络中最基础的模块选择。如下图b所示,作者选择卷积、ReLU、残差连接构建PlainNet的基础组件。
正则化
与图像复原任务不同,分类、检测、跟踪等high-level任务对正则化层十分敏感。因此,似乎正则化层对于图像复原神经网络也是重要的组成部分。通过实验,作者发现加入正则化层可以让PlainNet在去噪任务上提升0.44dB,在去模糊任务上提升3.39dB,且可以是训练更为平滑。因此,如上图c所示,作者进一步将layer normalization层加入原始模块。
激活函数
ReLU在复原网络中同样是一种常见的模块,但作者发现GELU能带来更好的性能收益,因此选择使用GELU替换原始模块的ReLU层。
注意力层
注意力机制可以说是近年来最火热的研究领域之一,其有效性得到了充分的验证,因此,作者选择将通道注意力机制加入到PlainNet中来,其结构如图3c所示。
Nonlinear Activation Free Network
在图3c所示模型的基础上,作者进一步分析了Gated Linear Units的适用性,这一模块在现有SOTA网络中同样得到了使用。
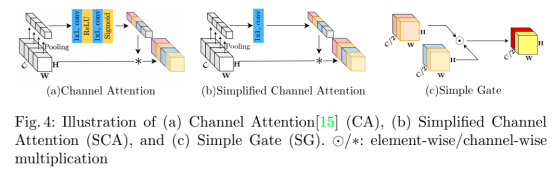
实验
在去噪数据集SIDD、去模糊数据集GoPro上,作者首先展开了消融实验。

从上表可以看出,PlainNet中每个模块、成分的添加都可以带来性能提升,符合文章的设计初衷。
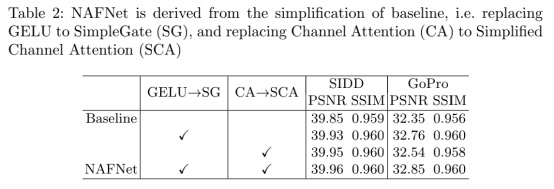
而在表2中,作者实验性地证明了NAFNet的最优计算量性质。
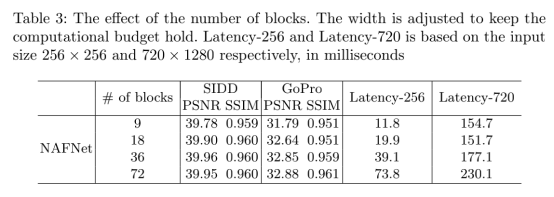
与表1、表2不同,表三则是验证了特征宽度,即channel数对性能和计算量对影响,不难发现,特征宽度并不会造成较大影响,这证明了NAFNet结构的鲁棒性和有效性。
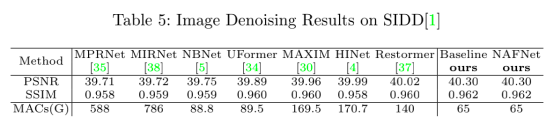
接着,作者展示了NAFNet与已有方法的比较结果。如下图所示,在去噪任务上,该模型取得了最佳指标和最好的视觉效果:


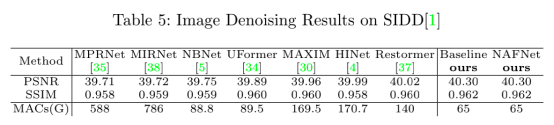
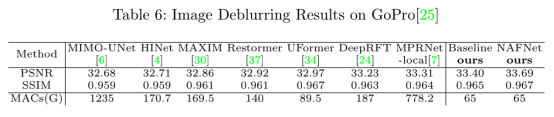
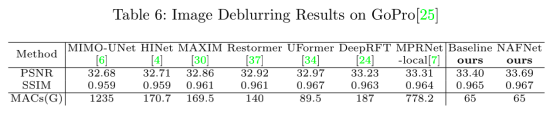
在去模糊任务上,作者发现即便是PlainNet也取得了SOTA的性能。

内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢