深度学习框架中的自动微分及高阶导数

1、高阶导数是怎么样的

先看一个 Stackoverflow 上关于如何用 PyTorch 计算高阶导数的最高票回答（https://stackoverflow.com/questions/50322833/higher-order-gradients-in-pytorch）：

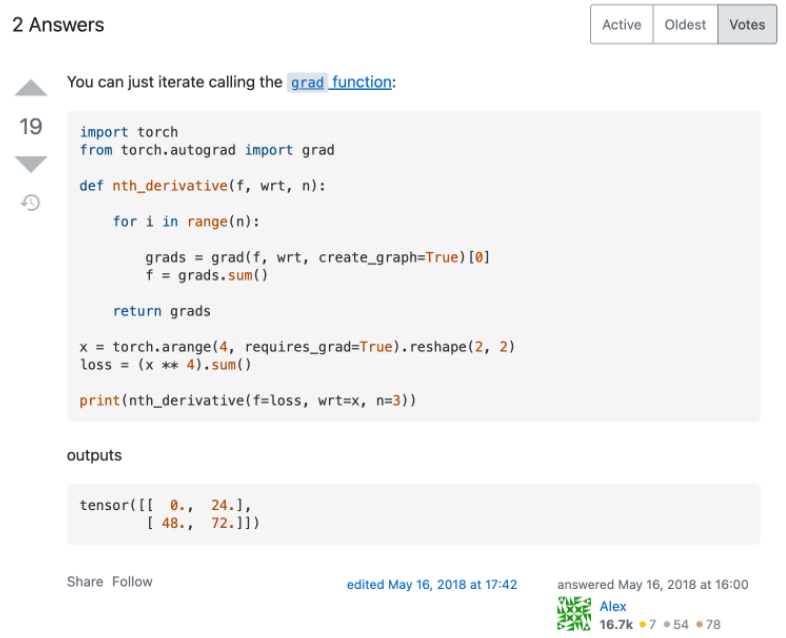
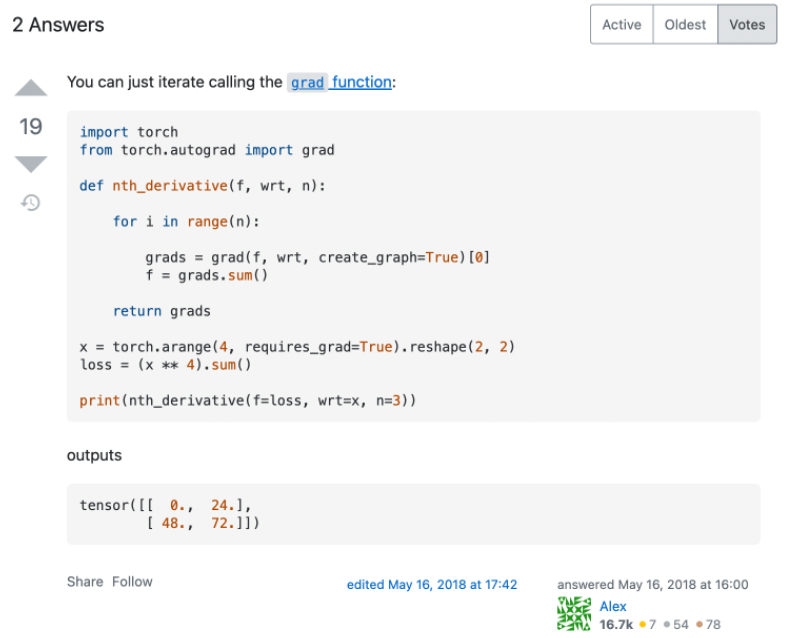
代码很简洁，结果看起来也是对的，然而实际上这个做法是有很大问题的，只是对于作者所测试的这类函数碰巧适用而已。那高阶导数实际上又该怎么计算呢？

这个问题的标准答案可能是：要看想计算的高阶导数是什么样的。平常的神经网络训练中，我们想让 loss 下降，也就是将 loss 作为损失函数”，所以求出一阶导数 $\partial loss/\partial w_{1}$ 、 $\partial loss/\partial w_{2}$ ......也就是 w1_grad、w2_grad......，并用它来更新 w1、w2......

如果我们现在有一个需求：想通过更新 w1、w2......来让反向传播得到的 w1_grad 尽可能低，也就是将 w1_grad 作为损失函数（在训练一些 GAN 网络时，不希望梯度的绝对值太大，就会有类似的需求），所以要计算 $（\partial w_{1}-grad)/\partial w_{1}$ 、 $（\partial w_{1}-grad)/\partial w_{2}$ ......也就是二阶导数 $\partial ^{2} loss/\partial w_{1}^{2}$ 、 $\partial ^{2} loss/(\partial w_{1} \partial w_{2})$ ......这可以用下面的 PyTorch 代码来简单的实现：

import torch
x = ...
loss = model(x)
w1_grad = torch.autograd.grad(outputs=loss, inputs=model.w1, create_graph=True)
w1_grad.backward()

不过，在大部分场景中想计算的二阶导数是另一种形式：

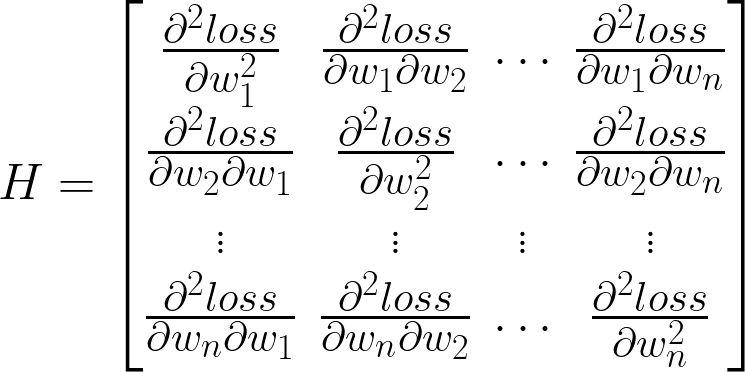
这个矩阵叫做 Hessian 矩阵。它是正儿八经的 “函数 loss = f(W) 的二阶导数”，即将神经网络看作一个输入为所有权重、输出为 loss 的多输入、单输出的函数 f （注意这里的输入不包括训练数据，因为训练数据实际上是固定的，是整个训练集，神经网络的训练就是通过改变 W 使在给定的训练集下的 loss 最低），对该函数 f 求导、再求导得到的结果。它可以用来判断某个 W 有没有让 loss 处于极小值点、极大值点或鞍点，它也是对 f(W) 做泰勒展开后二次项的系数的两倍，所以当我们想用一个二次函数来模拟神经网络，并根据二次函数的性质来更新 W、优化 loss 的时候（这个叫作牛顿法），也是一个绕不开的概念。

在很多场景，例如常用的优化方法共轭梯度法之中，这个矩阵还会和一个向量相乘，被称为 HVP（Hessian-Vector Product)。那么这个 Hessian 矩阵以及 HVP 该怎么求？一个容易想到的方法是：考虑到在上面那个希望 $w_{1}-grad$ 尽可能低的场景里，我们求出的 $\partial ^{2} loss/\partial w_{1}^{2}$ 、 $\partial ^{2} loss/(\partial w_{1} \partial w_{2})$ ......是这个矩阵的第一行，那只要对 N 个 $w_{i}-grad$ 都进行一次同样的过程，就能得到完整的 Hessian 矩阵了。再把这个矩阵乘以一个向量，就得到了 HVP。

这样是可行的，但是并不高效。特别是，如果只需要计算 HVP 而不是 Hessian 矩阵本身，其实是不用先把 Hessian 矩阵算出来，再计算和向量的乘积的，而是只需要进行两次反向传播，或者一次反向传播和一次“前向自动微分”就可以。具体的做法和原理，需要从反向传播背后的自动微分讲起。

2、自动微分

Reverse Mode（反向自动微分/反向传播）

自动微分分两种，reverse mode 和 forward mode。Reverse mode 就是大家熟悉的反向传播，在 PyTorch 中调用 loss.backward() 就可以执行，不过它的背后有一个大部分小伙伴都不了解的机制。先来看这个 PyTorch 代码：

import torch

x = torch.ones(2).requires_grad_()
y = x * 2

y.backward()

它会报错RuntimeError: grad can be implicitly created only for scalar outputs，即 y 不是一个标量。

如果我们给y.backward()传入任意一个形状和 y 相同的 tensor 作为gradient参数，如y.backward(gradient=torch.tensor([2, 3]))，这份代码就可以正常运行。

# 省略了定义 x 和 y 的代码
>>> y.backward(gradient=torch.tensor([2, 3]))
>>> x.gradtensor([4., 6.])

这背后的原因是，反向传播只能应用于一个单输出（即输出为标量）的函数。当我们设置 gradient 为 [2, 3] 时，PyTorch 会将 gradient 和 y 做内积，得到一个标量t = 2 * y[0] + 3 * y[1]，将标量 t 当作函数的输出并运行反向传播，因此 x.grad 的值是dt/dx，根据标量对矩阵的导数的定义容易得到dt/dy = [dt/d(y[0]), dt/d(y[1])] = [2, 3]，根据链式法则，dt/dx = dt/dy * dy/dx = [2, 3] * 2 = [4, 6]，所以 x.grad 的值会是 [4, 6]。

也就是说，对于任意一个 N 输出 M 输入的函数Y = f(X)（Y 是一个长度为 N 的向量），我们可以将 Y 和 v 做内积，得到一个标量 t 和一个单输出、M 输入的函数 g 满足t = g(X) = v * Y = v * f(X)，再通过反向传播求出函数 g 的梯度。

根据链式法则，函数 g 的梯度dt/dX等于dt/dY * dY/dX，而显然dt/dY就是向量 v，也就是 loss.backward() 函数中的 gradient 参数，dY/dX是函数f的导数（形状为 N*M 的 Jacobian 矩阵）。也就是说，以一个长度为 N 的向量 v 和一个 N 输出 M 输入的函数 f 为对象运行反向传播，可以求出向量 v 和函数 f 的导数的乘积，也就是 Vector-Jacobian Product，简称为 VJP。如果想用反向传播求出整个 Jacobian 矩阵，那么可以将 v 设置为第 i 个元素为 1，其它元素均为 0 的向量，这样就可以求出 Jacobian 矩阵的第 i 行，重复 N 次就可以求出整个矩阵。

......

（由于排版显示原因，其余内容请点击原文链接）

其他人都在看

欢迎下载体验OneFlow v0.7.0最新版本：https://github.com/Oneflow-Inc/oneflow/

内容中包含的图片若涉及版权问题，请及时与我们联系删除

深度学习框架中的自动微分及高阶导数

1、高阶导数是怎么样的

2、自动微分

Reverse Mode（反向自动微分/反向传播）

评论