近年来,人们对学习哈密尔顿方程的方法进行了大量研究。尽管这些方法非常有前途,但常用的哈密尔顿方程的表示方法使用广义动量,而广义动量一般是未知的。
因此,训练数据必须用这个未知的坐标系来表示,这给将模型应用于真实数据带来了困难。同时,哈密尔顿方程也有一个无坐标的表达方式,它是通过使用辛-2形式来表达的。
在这项研究中,我们提出了一个利用神经网络从数据中学习辛形式的模型,从而提供了一种从一般坐标系表示的数据中学习哈密尔顿方程的方法,这种方法不限于广义坐标和广义动量。
因此,所提出的方法不仅能够对哈密尔顿和拉格朗日形式的目标方程进行建模,而且还能够提取隐藏在数据中的未知哈密尔顿结构。例如,许多多项式常微分方程,如Lotka-Volterra方程,已知其存在非微观的哈密尔顿结构,我们的数值实验表明,这种结构当然可以从数据中学习。
从技术上讲,每个辛2-形式都与一个偏斜对称矩阵相关,但并非所有的偏斜对称矩阵都定义了辛2-形式。在所提出的方法中,利用辛2-形式是某些微分1-形式的外导数派生,我们用神经网络对微分1-形式进行建模,从而提高了学习的效率。
本次研究的主题是神经辛形式模型,我们将用这个模型学习一般坐标系下的哈密尔顿方程。
Deep learning for physical simulation
深度学习在物理学模拟领域
Learn dynamical system 学习动力系统
- 物理学模拟具有广泛的应用
- 数据驱动方法是一种常用的加速仿真的方法
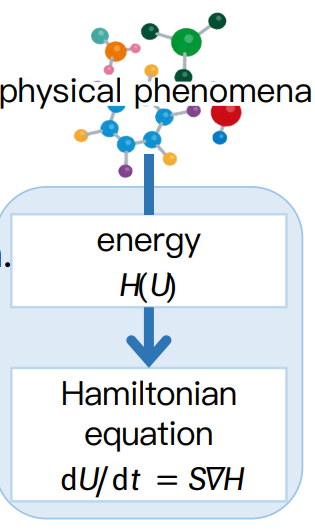
- 物理现象可用基于物理定律的微分方程表示
- 遵守物理定律保证了结果的可靠性

在计算机上对这些现象进行建模和模拟的时候,最简单的方式就是用神经网络从数据中学习代表运动方程的常微分方程右边部分,也就是我们常说的Neural ODE模型。
但由于神经网络的通用性,能量守恒等物理规律在这个模型中可能是不成立的。为了不使物理特性消失,因此把这些特性引入研究模型之中。
近年来,学者们对这些模型也进行了研究,比如Euler-Lagrange equation and Hamilton equation。
学习物理现象,同时保留物理定律
Lagrangian Neural Network (LNN)
用来学习拉格朗日动力学运动方程的模型叫做拉格朗日神经网络。
- Lagrangian system (the Euler-Lagrange equation)在这个网络中,一个神经网络被用来对拉格朗日L进行建模,并从中推导出运动方程。在拉格朗日力学中,方程是用状态变量及其时间导数来描述的。这也使得我们学习所需要的数据较为容易来准备。
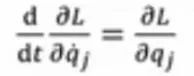
- 该模型还存在一个特点,在tangent bundles切线束上定义了一个系统。
- 该模型被限制在一个特定的结构之中且该结构属于哈密尔顿方程的一部分。
Hamiltonian Neural Network (HNN)
哈密尔顿神经网络是一个比较有名的模型,这是用来学习哈密尔顿动力学运动方程的神经网络。在该网络中,一般会假设采用以下形式的模型。
- 哈密尔顿动力学系统
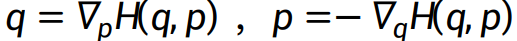
- 由于哈密尔顿方程本身就存在守恒定律,因此哈密尔顿神经网络也遵循能量守恒。
- 由于能量守恒定律的存在,方法在长期预测中也有良好的表现。
- 这个方法也可以被扩展为各种形式的模型,尤其是structure-preserving numerical integrators和discrete gradient method。
不过,虽然这种模型在以往的研究中也常常被应用,但是哈密尔顿方程只有在正则坐标下才拥有这样的形式。
同时,这个坐标系也取决于能量函数H,这个H是一个未知的哈密尔顿方程。所以说,这个坐标系中很难去事先准备数据,也很难将这个模型应用到实际问题之中。

在一般坐标系中,通过斜对称矩阵,哈密尔顿方程可以被转换成这种形式。但因此在一般坐标系下学习哈密尔顿动力学方程的方式是研究斜对称矩阵S(u),如果方程是按上图中的形式给出,那么就有可能显示出能量守恒定律。这种方法也被称为Skew symmetric matrix learning。但是这种方法也存在缺点,斜对称矩阵必须满足一定的几何条件。
在斜对称矩阵通过神经网络去学习的时候,模型可能不是哈密尔顿方程;在这种情况下能量可能是守恒的,但是物理规律可能是不成立的。另外,如果研究的对象是用哈密尔顿方程来进行描述的,那么学习的结果是非哈密尔顿方程,那么说明是一个效率很低的学习。
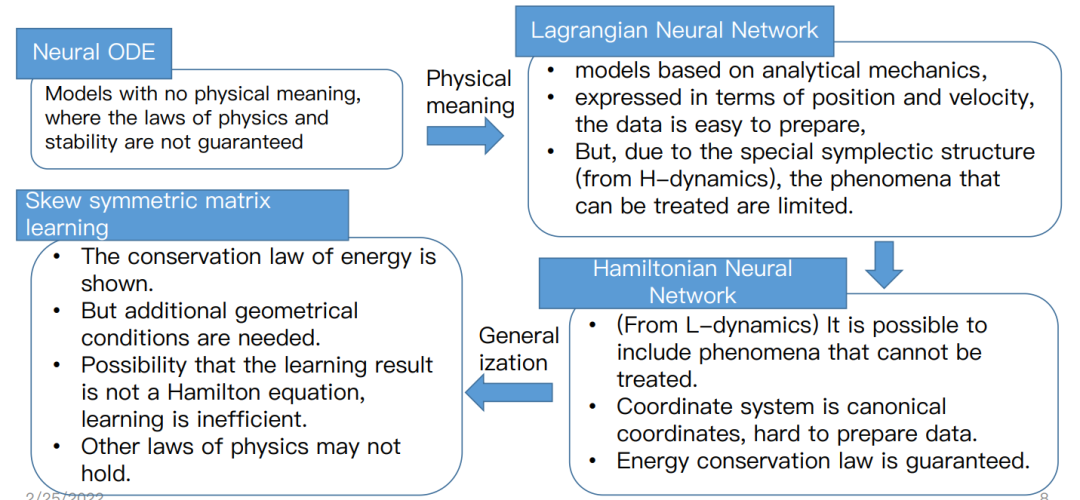
总结一下,现有学习常微分方程的基本方法是Neural ODE,但是这种方法没有物理意义,其物理定律和稳定型均得不到保证。其中分析力学提出了哈密尔顿神经网络,拉格朗日的运动方程是用位置和速度来表示的,虽然很容易准备数据,但是其几何结构却是有限的,和哈密尔顿相比能够处理的现象也是有限的。
而哈密尔顿力学可以包含拉格朗日力学不能包含的现象,但是正则坐标却被未知函数而阻碍,导致很难去准备数据。在一般坐标系中的表现,哈密尔顿方程是对斜对称矩阵学习,而在这个模型之中:能量守恒定律是可以保证的,不过需要额外的几何条件。如果学习的结果不能成为哈密尔顿方程,那么这个学习就是没有效率的。同时,其物理规律也有可能是不成立的。
2 Proposal :Neural Symplectic Form
为了解决上述问题,我们提出了以下模型,即使用神经网络来学习Neural Symplectic Form。这使得我们有可能从不局限于广义坐标和动量的一般坐标系所表示的数据中去学习哈密尔顿方程。关键是要利用哈密尔顿方程与坐标系无关的形式,毕竟之前研究的局限性在于坐标系通常会被固定为广义坐标。
然而在几何力学的研究中,方程里的ω被称为Symplectic Form。它对应于一个斜对称的矩阵,因此通过学习Symplectic Form与哈密尔顿方程,我们可以从数据中学习任何坐标系中的方程。
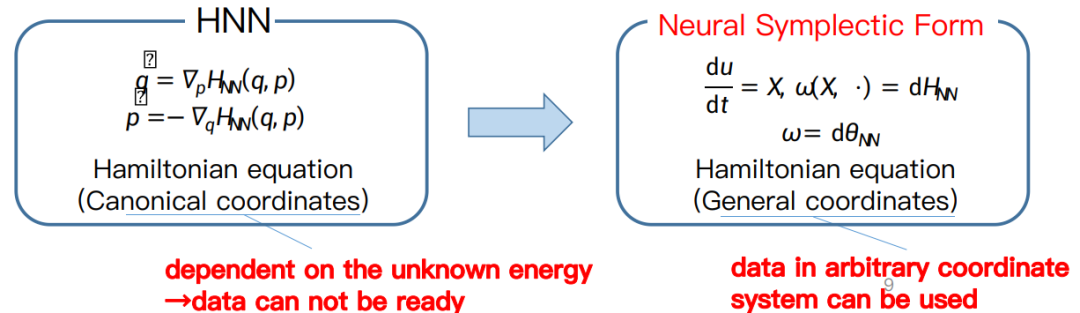
因此,我们提出的方法不仅能对一般坐标系中的方程进行建模,而且能够提取隐藏在数据中未知的哈密尔顿结构。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢