【论文标题】Pre-training helps Bayesian optimization too
【作者团队】Zi Wang, George E. Dahl, Kevin Swersky, Chansoo Lee, Zelda Mariet, Zachary Nado, Justin Gilmer, Jasper Snoek, Zoubin Ghahramani
【发表时间】2022/04/29
【机 构】谷歌
【论文链接】https://arxiv.org/pdf/2109.08215v3.pdf
【代码链接】https://github.com/google-research/hyperbo
贝叶斯优化(BO)已经成为许多现实世界函数的全局优化的流行策略。与人们普遍认为BO适合优化黑箱函数相反,它实际上需要关于这些函数特征的领域知识才能成功部署。这种领域知识通常表现为高斯过程先验,它规定了对函数的初始置信。然而,即使有专家知识,选择一个先验也不是一件容易的事。这对于复杂的机器学习模型的超参数调参问题来说尤其如此。本文寻求一种替代性的做法来设置这些函数先验,在有类似数据的情况下,可以预训练一个更严格的分布。理论上,本文显示了预训练预设的BO的bounded regret。为了在现实的模型训练设置中验证,作者收集了一个大型的多任务超参数优化数据集,在流行的图像和文本数据集以及蛋白质序列数据集上评价,结果表明,本文的方法能够比最好的竞争方法至少有效地找到好的超参数。
工程师和研究人员如何从过去的经验中学习如何设置好的先验很重要,本文试图通过对不同但相关的任务的数据进行先验预训练,使先验确定过程自动化,这种先验预训练方法也被称为先验学习或元学习的一个版本。对于现实世界大数据问题,很难理解目标的landscape阻碍了贝叶斯优化的使用,几乎无法获得专家对先验的干预。
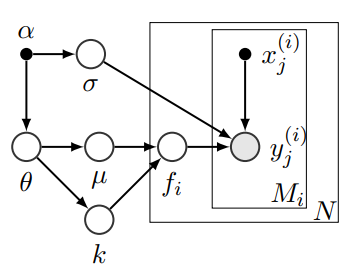
上图展示了基于贝叶斯的层次高斯过程的图模型,假设超参数优化任务的整体设置由参数θ∼p(θ;α)定义;均值和核函数μ和k从p(μ, k | θ)中抽取。独立函数样本{fi}i∈[N]本身就是从GP(µ, k)中抽取的。包含以下部分:
- 从p(θ; α)中抽取GP参数θ,从p(σ; α)中抽取观测噪声参数σ。
- 从p(µ, k | θ)中抽取平均函数µ和核函数k。
- 对于从1到N的每个任务i,从GP(µ, k)中抽出一个函数fi;对于从1到Mi的每个数据点j,给定输入x(i)j,得到观察值y(i)j∼N(fi(x(i)j), σ2)。

上图展示了HyperBO,该方法在一组有代表性的数据集上训练GP超参数,并在优化过程中固定它们。HyperBO分两步运行。首先,学习一个GP模型来近似生成数据集的基础真实GP。然后,用学到的做标准的BO来优化一个新函数。
目标是获得参数θ的点估计值ˆθ,需要估计均值函数µˆ和核ˆk,它定义了学习模型GP(ˆµ, ˆk)。在上图的BO迭代过程中,我们更新条件GP,但不重新估计GP的平均值和核。通过分离条件GP更新和GP参数训练的数据,HyperBO将计算成本降到最低,同时在理论上和经验上都保持了良好的性能。此外,本文避免了BO鸡和蛋的困境,即搜索策略是在BO过程中收集的数据上训练的,而数据点是由搜索策略选择的。
HyperBO有几个变体,包括使用不同的获取函数和不同的目标。一般使用阈值的概率提升(PI)作为获取函数PI为α,对应图模型中PI设定为α
- H* NLL:以PI为获取函数的HyperBO,以负边际似然为目标进行预训练。
- H* KL:以PI为获取函数的HyperBO,以匹配数据点的K散度为目标进行预训练。
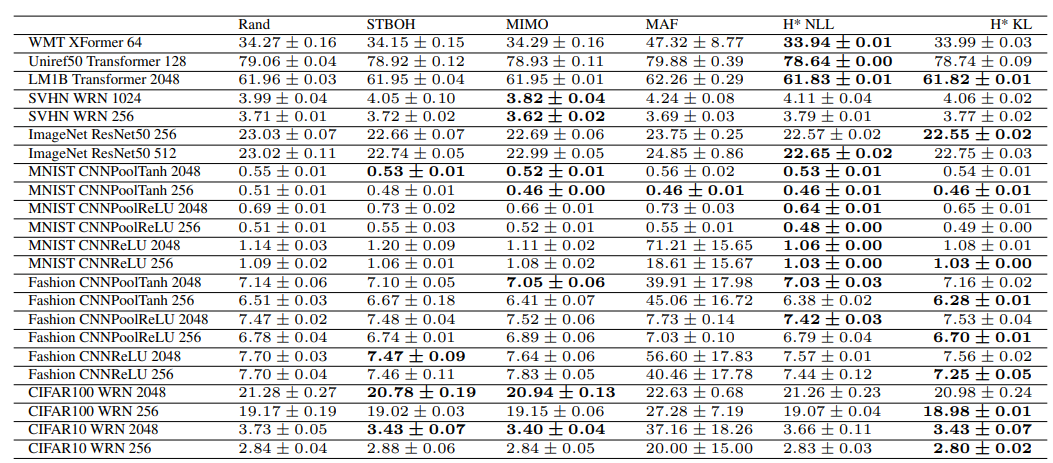
为了进行经验验证,本文首先收集了一个由各种深度神经网络训练任务的超参数评估组成的数据集。这些任务包括在图像、文本和其他数据集上优化深度模型。然后,将本文的方法与深层神经网络优化器中现实的超参数调整场景中的几个竞争基线进行了比较,以更好地理解HyperBO的特性。
上图展示了离线优化器超参数优化实验中每个测试任务的最佳验证错误率的平均值和标准误差(%)。包括MIMO和HyperBO变体(H* NLL和H* KL)在内的Meta BO方法可以获得与测试任务不相同的任务数据集的训练任务。本文展示了随机搜索和前5种方法的结果,可以看的HytperBO得到了较好的结果。黑体字强调了最低错误率。对比方法包括:
- Rand。在搜索空间中进行随机搜索。
- STBO:具有恒定平均函数、Matern内核和PI获取函数的单任务BO。每一次BO迭代,STBO都通过测试任务的第二类最大似然来优化GP超参数。这个实现对应于基本的现成的BO设置。
- STBOH:单任务GP-UCB(系数=1.8),具有恒定的平均值、Matern核和包括UCB系数在内的超参数的手工调整先验
- MIMO。多任务BO与GP基础作为共享子网络的前馈神经网络的集合。
- RFGP:以GP作为随机特征的多任务BO。
- MAF:为了避免混淆,本文将Volpp(2020)的元BO方法称为MAF(元获取函数)。MAF使用强化学习,在一组迁移学习任务上学习由神经网络建模的获取函数。
创新点
一种新的BO的先验预训练方法,在保留理论保证的同时做出最小的假设.
一个大型的多任务超参数调整数据集,不仅有利于本文方法,而且可以作为一个现实的基准来测试未来的方法。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢