ICLR 2022 | 视频中的动态卷积TAdaConv以及高效的卷积视频理解模型TAdaConvNeXt

论文名称

TAda! Temporally-Adaptive Convolutions for Video Understanding

论文链接：

https://arxiv.org/pdf/2110.06178.pdf

项目主页：

http://tadaconv-iclr2022.github.io

代码链接：

https://github.com/alibaba-mmai-research/TAdaConv

 

导读

相较图像而言，视频中包含了更大量的信息，也通常需要更多的计算资源来进行处理。因此，如何高效地对视频中的内容进行理解成为了视频理解中的关键研究方向之一。

今天给大家介绍TAdaConv，一种在行为识别模型中即插即用的时序自适应卷积（Temporally-Adaptive Convolutions）。作为2D/3D卷积的增强版，TAdaConv可以明显提升SlowFast、R2D和R3D等任何使用2D/3D卷积的模型性能，而额外的计算量可以忽略不计。在Kinetics-400，Something-Something-V2以及Epic-Kitchens-100视频分类任务上，基于TAdaConv构建的TAda2D和TAdaConvNeXt均达到了极具竞争力的性能。

此外，作为一种高效引入时序上下文的方式，TAdaConv也在视频分类以外的任务得以应用。在CVPR 2022 TCTrack: Temporal Contexts for Aerial Tracking 中，TAdaConv被拓展为Online-TAdaConv，并被展示可以被用于目标跟踪网络来提取带有时空上下文的特征，从而提升目标跟踪器的性能。

 

贡献

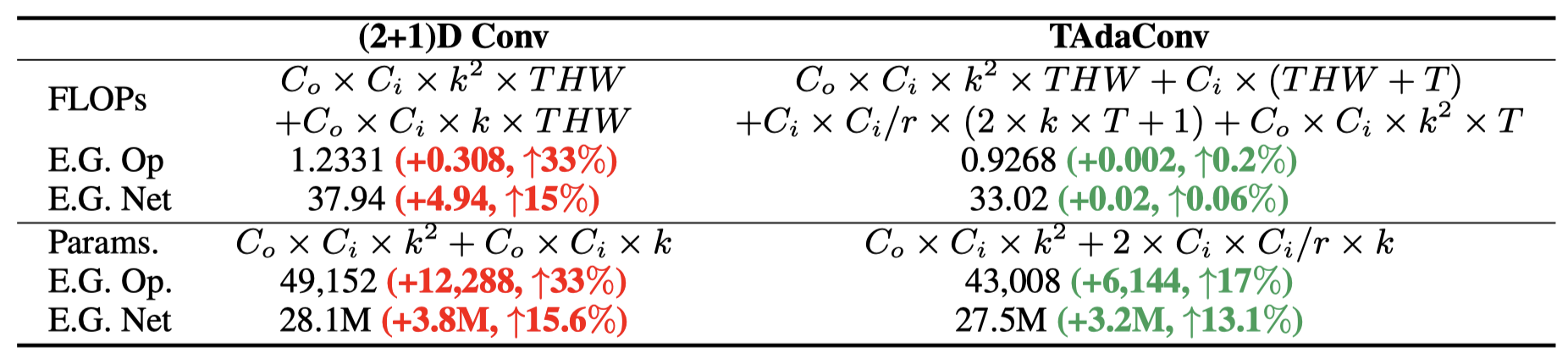
自从P3D[1]和R(2+1)D[2]分别在17年的ICCV和18年CVPR上被提出之后，很大一部分工作的时序理解都是通过在时间轴上的1D conv完成的，包括而它的复杂度是O(C^2xKxTHW)。这种基于像素点的操作，会在纯2D conv的基础上带来不可忽视的计算开销。举例来说，对于K=3的2D和1D conv，1D conv会在2D conv的基础上将计算量提高33%。

因此，我们思考，是否有一种方式直接让2D conv有时序的建模能力呢？

回顾2D conv，平移不变性（translation invariance）或者说空间不变性（spatial invariance）是卷积取得巨大成功的重要原因之一[3]。因此在视频模型中，大部分模型在使用2D conv的时候对不同帧的不同位置都采用共享的权重，以达到时空不变性（spatiotemporal invariance）。然而，最近在图像中的一些研究发现，这种严格的权重共享实际是一种过强的inductive bias，而适当地放松一些这种不变性，能让模型有更好的空间建模能力[4][5]。

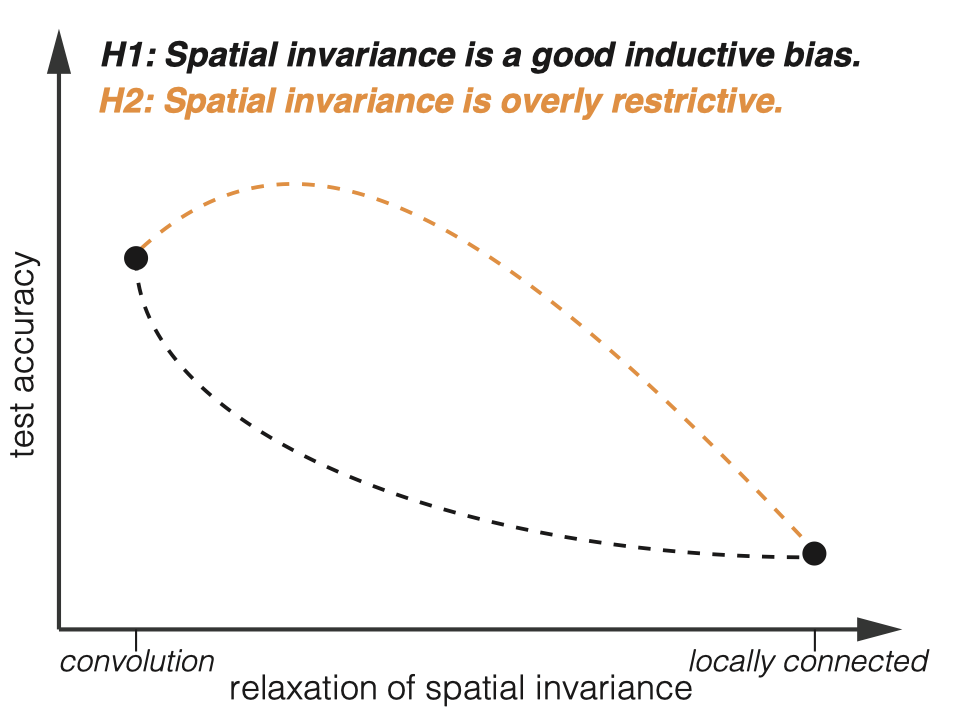
因此，我们假设：放松卷积的时序不变性（temporal invariance）可以增强卷积的时序建模能力。基于该假设，我们提出时序自适应卷积（TAdaConv）来代替传统视频模型中的卷积，并分别基于ResNet和ConvNeXt构建高效的视频模型TAda2D以及TAdaConvNeXt。

 

方法

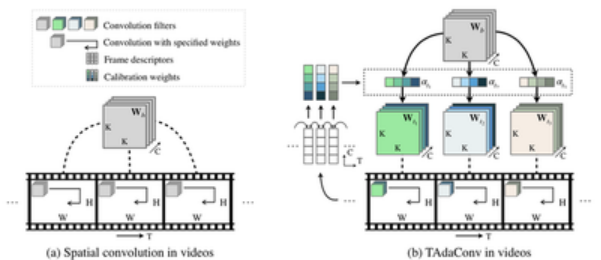
对于空间卷积而言，时序不变性体现在空间卷积的权重在视频的每一帧中是共享的（如下图(a)所示）。因此，要放松时序上的不变性，TAdaConv在不同的视频帧中使用不同的卷积权重（如下图(b)所示）。

具体来说，TAdaConv将每一帧的卷积核 \( \mathbf{W}_t \)分解为一个基权重（base weight）和一个校准权重（calibration weight）的组合：

\( \mathbf{W}_t = \alpha_t\cdot \mathbf{W}_b \)​

其中，基权重 \( \mathbf{W}_b \)由视频帧共享，而校准权重 \alpha_tαt​ 则对于每一帧独立，并根据输入来进行生成。

这么做有三点好处：

1. TAdaConv可以是即插即用的，并且模型的预训练权重可以仍然被保留和利用；
2. 由于校准权重的存在，卷积的时序推理能力得以增强，空间卷积被赋予时序推理能力；
3. 相较时序卷积而言，由于时序卷积是在特征图上的操作，而TAdaConv是在卷积核上的操作，TAdaConv更加高效。

 

2.2 校准权重的生成 Generation of calibration weights

下一个问题就是，如何获得对于每一帧不同的校准权重 \( \alpha_t \) ？我们考虑了很多种方法，包括使用可学习（learnable）参数，或者基于全局描述子生成 TT 个校准权重。最后我们发现，为了更好地进行时序建模，校准权重的生成过程也需要考虑到时序上下文信息，也就是 \( \mathbf{x}_t^{\text{adj}}=...,\mathbf{x}_{t-1},\mathbf{x}_t,\mathbf{x}_{t+1},... \)。

在实际的校准权重生成过程中，我们考虑两种时序上下文。分别是局部的时序上下文和全局的上下文。为了保证生成过程的高效性，校准权重基于帧描述子（frame descriptor）\( \mathbf{v}_t=\text{GAP}_s(\mathbf{x}_t) \)来进行生成，而不是基于帧的特征。其中，对于局部的时序上下文，我们使用两个1D卷积完成：

\( \mathcal{F}(\mathbf{x}_t^{\text{adj}})=\text{Conv1D}^{C/r\rightarrow C}(\delta(\text{BN}(\text{Conv1D}^{C\rightarrow C/r}(\mathbf{v}_t^{\text{adj}})))) \)

全局的上下文 \mathbf{g}g 则是通过一个线性映射（FC)叠加到帧描述子上：

\( \mathcal{F}(\mathbf{x}_t^{\text{adj}}, \mathbf{g})=\text{Conv1D}^{C/r\rightarrow C}(\delta(\text{BN}(\text{Conv1D}^{C\rightarrow C/r}(\mathbf{v}_t^{\text{adj}}+\text{FC}^{C\rightarrow C}(\mathbf{g}))))) \)

这个生成过程可以如下图(b)所示。

 

2.3 校准权重的初始化 Initialization of calibration weights

相比于已有的动态卷积方法，为了能更好地利用预训练的权重，我们精心设计了TAdaConv校准权重的初始化，以保证在初始状态下，TAdaConv完全保留预训练的权重。具体地，在校准权重生成函数初始化的时候，最后一层1D卷积的权重被初始化为全零，并且加上了一个1以保证全1的输出：

\( \alpha_t=\mathcal{G}(\mathbf{x})=\mathbf{1}+\mathcal{F}(\mathbf{x}_t^{\text{adj}}, \mathbf{g}) \)

在这样的初始状态下，动态卷积的权重 \( \mathbf{W}_t=\mathbf{1}\cdot\mathbf{W}_b=\mathbf{W}_b \)​ ，与预训练载入的权重Wb​ 相同。

对比(2+1)D Conv，TAdaConv在操作层面和模型层面都有明显的计算量和参数优势：

 

2.4 校准权重的维度 Calibration dimension

对于一个基权重Wb​ 来说，它的维度通常是 \( C_{\text{out}}\times C_{\text{in}} \times k^2 \)，因此有三个维度可以用来校准。我们将校准维度设置为 \( C_{\text{in}} \)。

 

03. 在视频模型中使用TAdaConv

具体代码实现请见TAdaConv repo。

# 1. copy models/module_zoo/ops/tadaconv.py somewhere in your project #    and import TAdaConv2d, RouteFuncMLPfrom tadaconv import TAdaConv2d, RouteFuncMLP

class Model(nn.Module):

  def __init__(self):




    ...




    # 2. define tadaconv and the route func in your model

    self.conv_rf = RouteFuncMLP(

                c_in=64,            # number of input filters

                ratio=4,            # reduction ratio for MLP

                kernels=[3,3],      # list of temporal kernel sizes

    )

    self.conv = TAdaConv2d(

                in_channels     = 64,

                out_channels    = 64,

                kernel_size     = [1, 3, 3], # usually the temporal kernel size is fixed to be 1

                stride          = [1, 1, 1], # usually the temporal stride is fixed to be 1

                padding         = [0, 1, 1], # usually the temporal padding is fixed to be 0

                bias            = False,

                cal_dim         = "cin"

            )




     ...




  def self.forward(x):




    ...

    

    # 3. replace 'x = self.conv(x)' with the following line

    x = self.conv(x, self.conv_rf(x))




    ...

 

04. TAda2D & TAdaConvNeXt 网络

基于ConvNeXt[6]和ResNet，我们分别构建TAdaConvNeXt和TAda2D视频模型。针对ConvNeXt，我们直接将ConvNeXt中的2D depthwise卷积替换为depthwise TAdaConv，并遵循大部分已有的基于transformer的视频模型，使用3D的tokenization方法。针对ResNet，由于基于ResNet的视频模型通常使用2D stem，我们额外提出一种基于average pooling的时序信息聚合方式，连接在TAdaConv之后：

\( \mathbf{x}_\text{aggr}=\delta(\text{BN}_1(\mathbf{\tilde{x}})+\text{BN}_2(\text{TempAvgPool}_k(\mathbf{\tilde{x}}))) \)

 

实验

实验中，针对TAdaConv，TAda2D和TAdaConvNeXt，我们在两个任务，一共5个数据集上进行评估。

5.1 假设验证

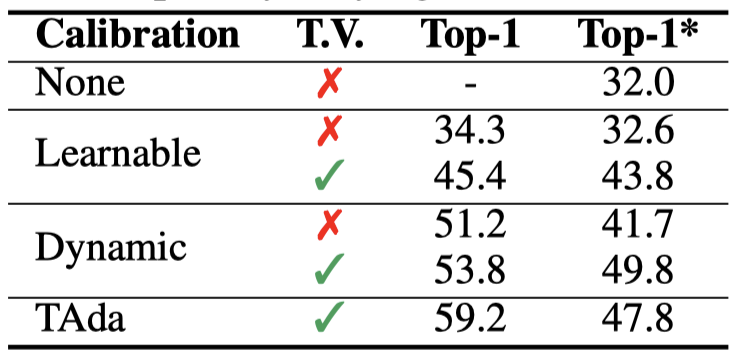
我们首先对放松时序不变性可以提升时序建模能力进行验证。我们采用了3种校准权重生成的方式，分别为learnable calibration，dynamic calibration和我们的TAda。对于learnable和dynamic，我们又分为两种，分别为是否temporally varying（T.V.），T.V.代表对不同的帧，卷积权重不同（也就是放松了temporal invariance）。从下表可以得出以下结论

1. 可学习校准，相较没有校准权重的baseline来说有一定的提升（2.3%），而如果放松temporal invariance，那么性能提升会达到13.4%
2. 动态校准即使在严格的temporal invariance约束下，也会在baseline上有更大的提升（19.2%），进一步放松temporal invariance，性能可以得到进一步提升（21.8%）
3. TAdaConv结合局部和全局时序上下文的校准权重生成方式性能最优（59.2%）

这也证明了，适当地放松temporal invariance是可以对时序建模有益的。

5.2 插入实验

可以看到，将TAdaConv放到主流的视频卷积网络上，包括R(2+1)D[2], R3D[7], SlowFast[8]，都可以看到可观的涨点。其中在kinetics400上平均提升约1.3%，在something-something-v2数据集上平均提升约2.8%，在epic-kitchens上平均提升1%以上。与此同时，计算量的增加仅为0.01~0.02GFlops。

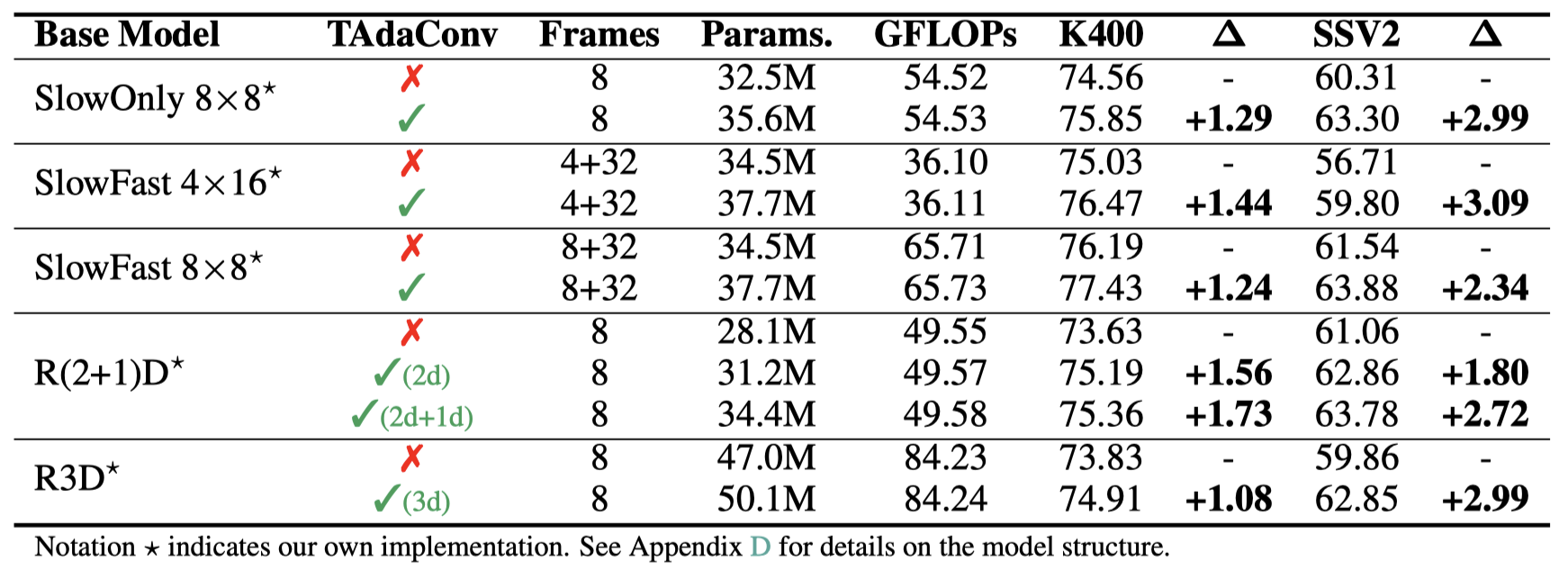
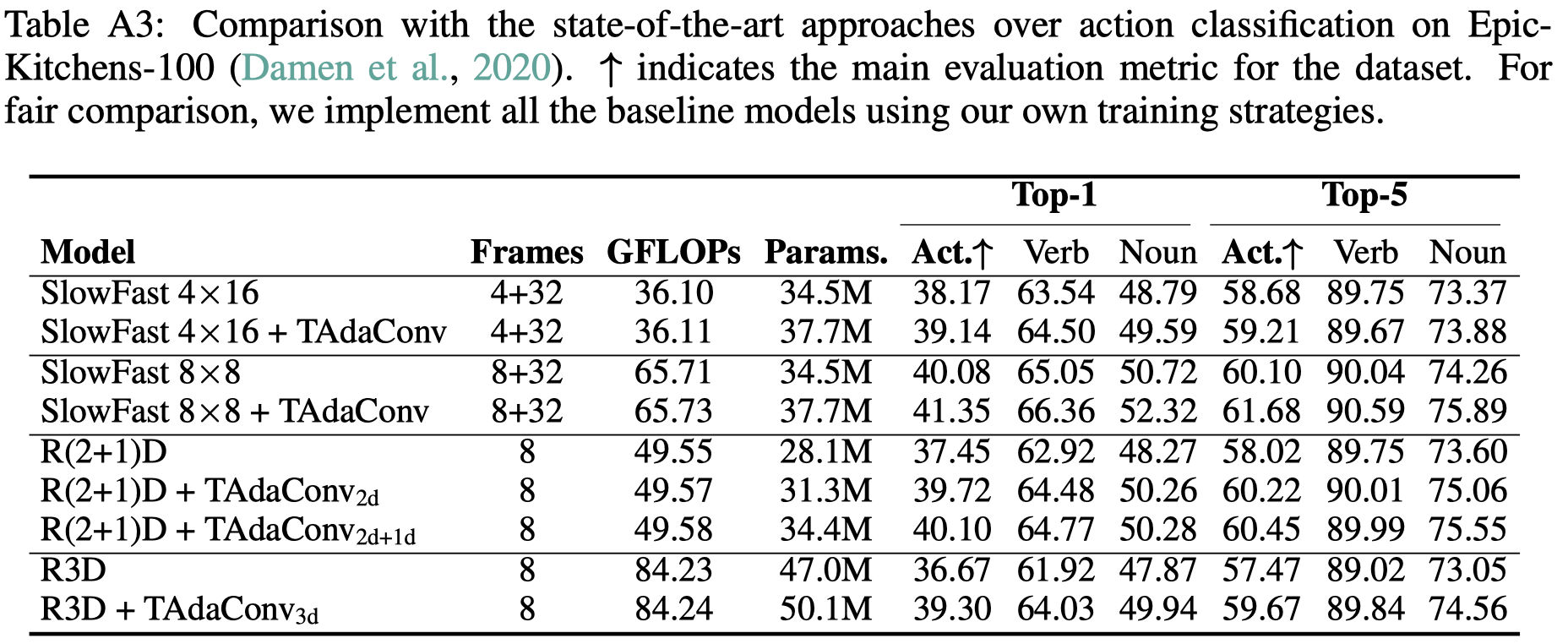
5.3 动作识别上的结果

我们主要在Kinetics-400、Something-Something-V2以及Epic-Kitchens-100上进行动作识别的评估。TAda2D对比已有的卷积视频模型有较好的性能和计算量的tradeoff，而TAdaConvNeXt则相对最近基于transformer的视频模型有一个极具竞争力的性能。

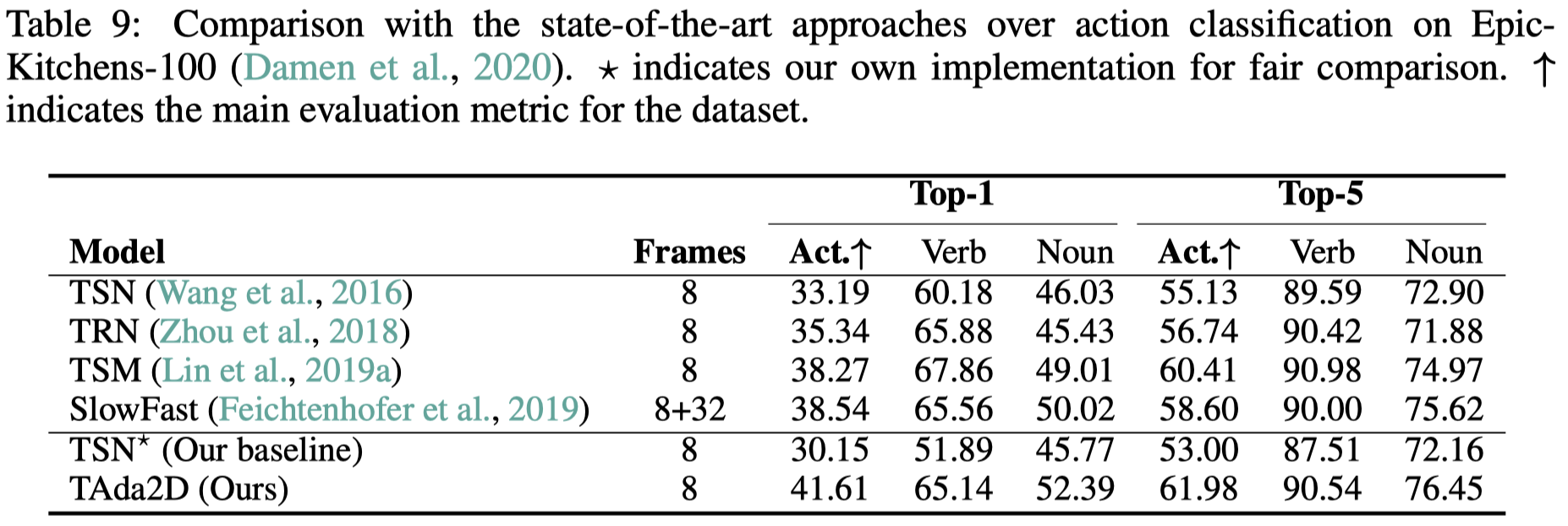
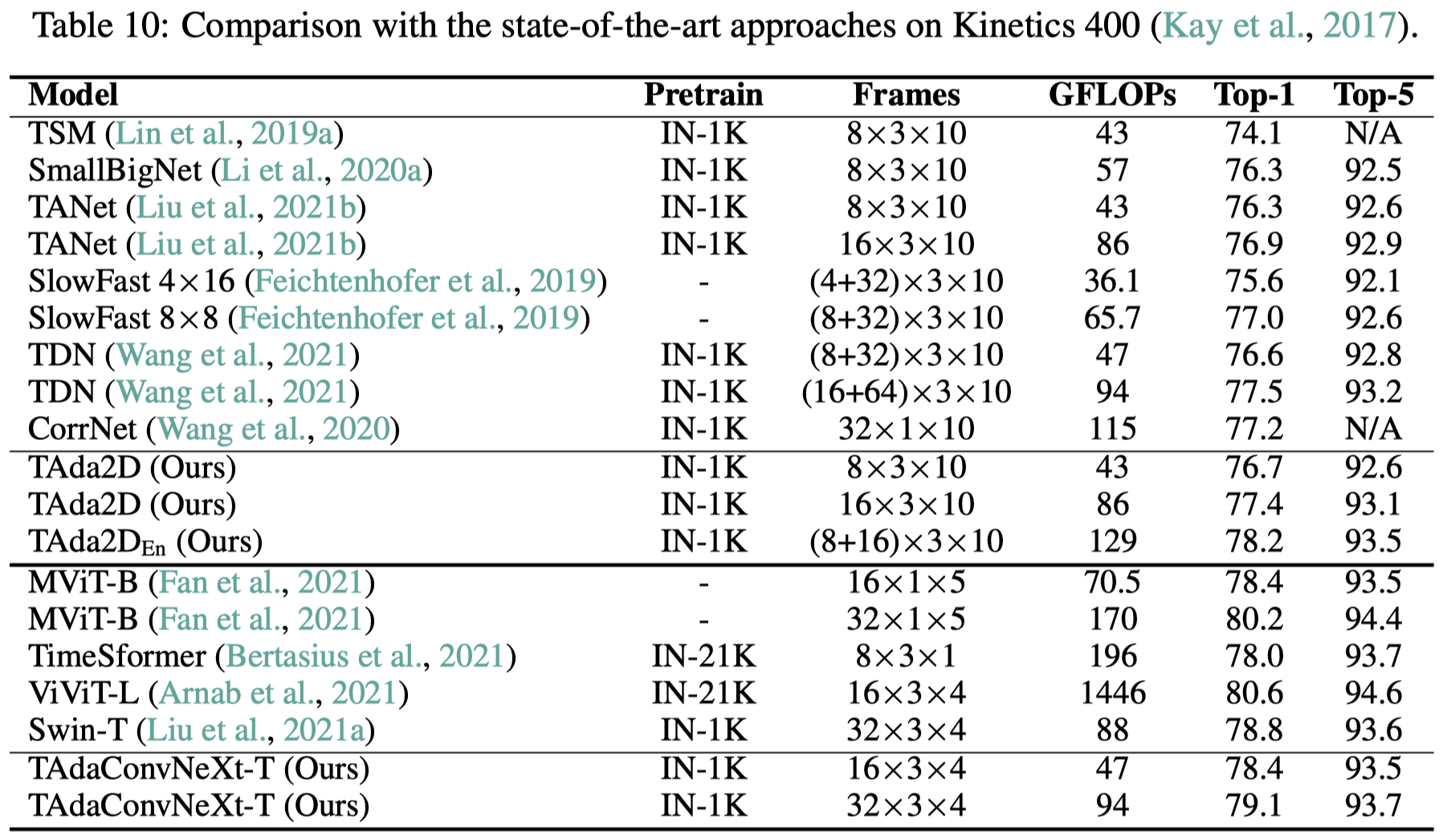
5.4 时序动作定位上的结果

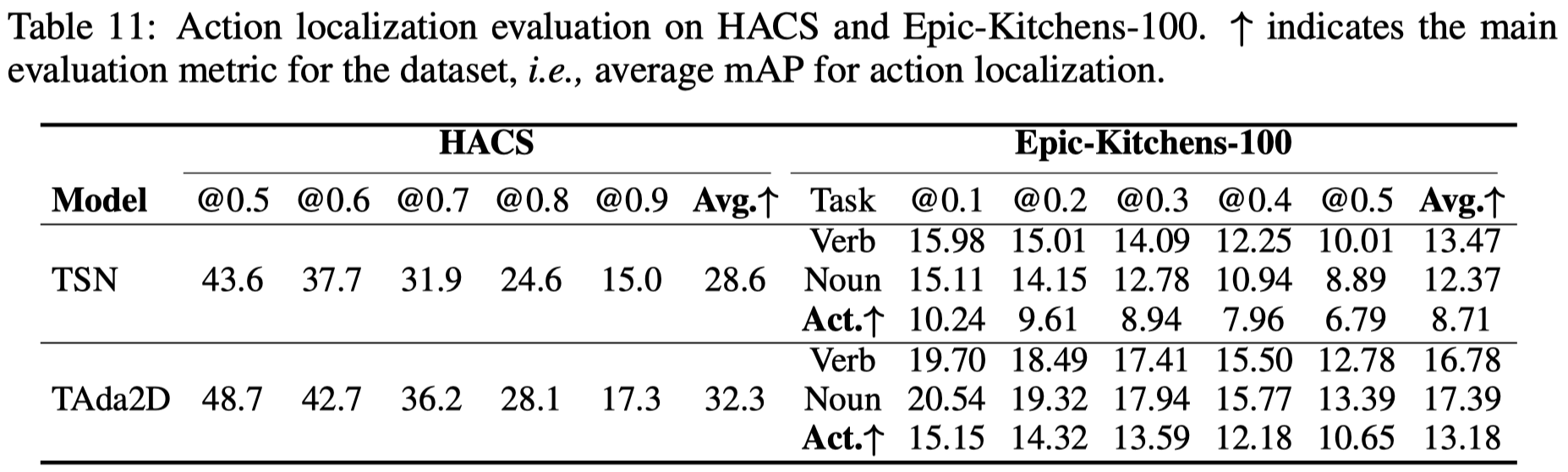
在时序动作定位任务上，我们在HACS和Epic-Kitchens-100上进行评估。对比baseline TSN，TAda2D提供的特征在两个数据集上均有5%的mAP提升。

5.5 消融实验

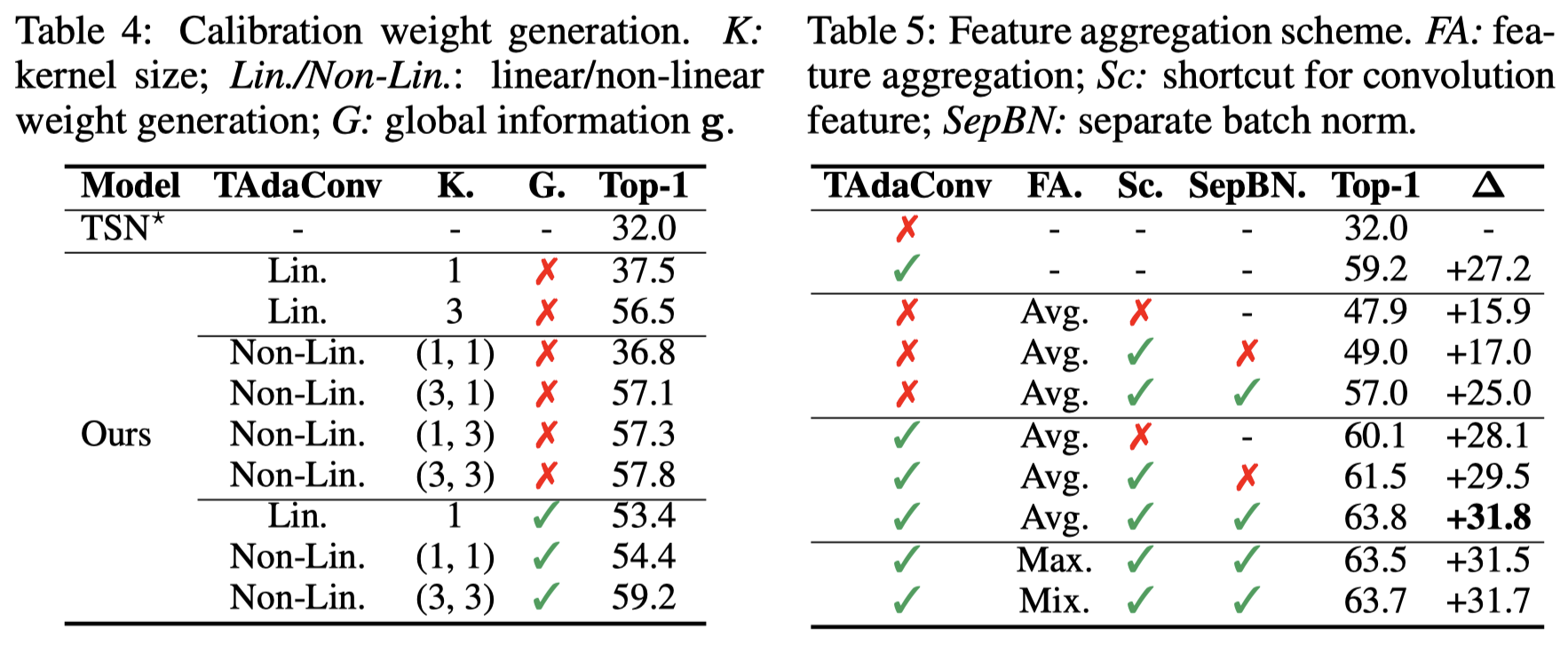
我们对TAda的校准权重生成（calibration weight generation）的过程进行消融实验（Table 4）。我们发现，在校准权重生成的过程中，考虑时序上下文是TAdaConv性能提升的关键。在baseline的基础上，使用两个1D Conv (Non-Lin.) 基于局部上下文生成校准权重，可以带来25.8%的性能增益，而单纯考虑全局上下文可以带来17.6%（54.4 vs. 36.8）的性能增益。两者结合，在baseline的基础上可以带来27.2%的性能增益。

进一步加入时序信息聚合，我们发现，对于avg pooling之后的特征使用不同的batchnorm，对比相同的batchnorm可以带来8%的性能增益。

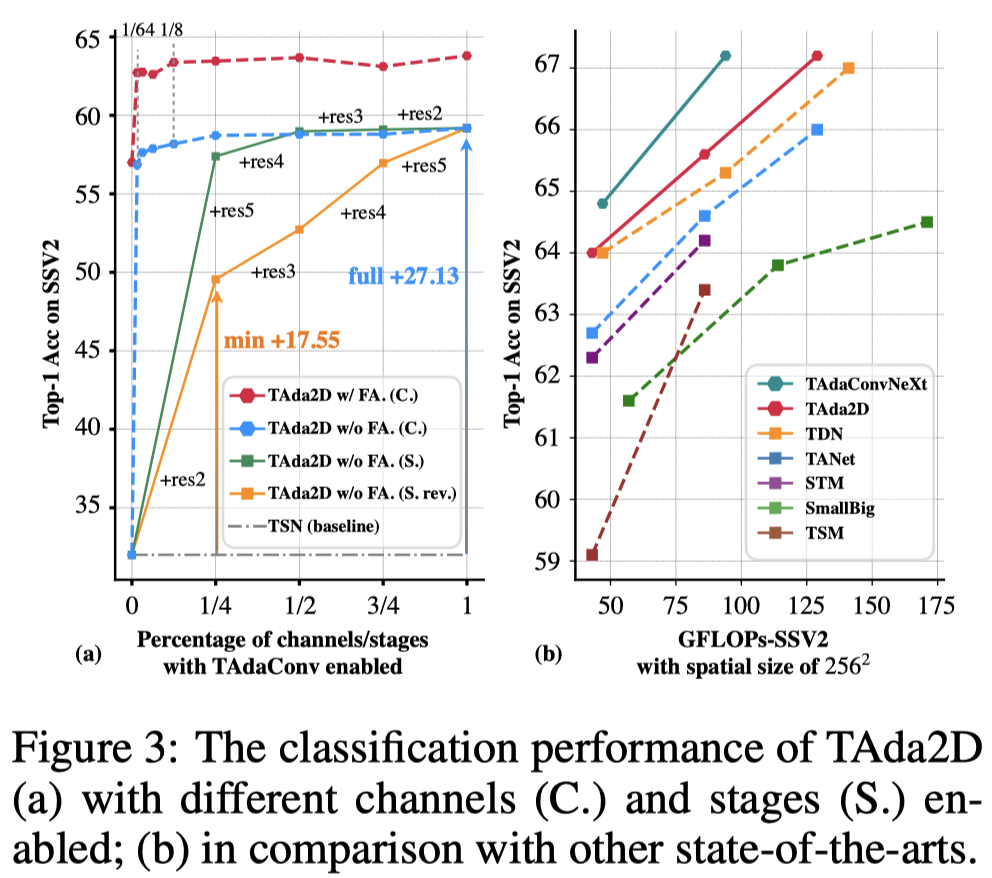
我们尝试在不同的stage，在不同数量的channel上将2D conv替换为TAdaConv（左图）。我们发现，仅仅使用1/64的通道就足以让网络的时序建模能力大大提升。而对于不同的stage来说，在网络更深处将2D conv替代为TAdaConv带来的增益更大。相比已有的视频模型（右图），TAda2D和TAdaConvNeXt达到了最优的性能和计算量的tradeoff。

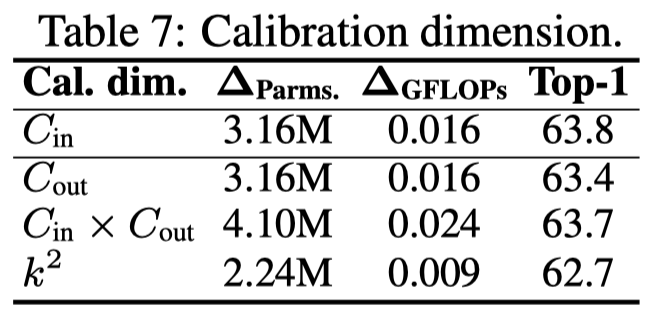
对于校准维度来说，我们发现对输入通道进行校准的性能提升最大。但只要进行了校准，性能都相差不多。

 

参考文献

[1] Learning spatio-temporal representation with pseudo-3d residual networks, in ICCV, 2017.

[2] A closer look at spatiotemporal convolutions for action recognition, in CVPR 2018.

[3] Natural image statistics and neural representation, in Physical review letters 1994.

[4] Revisiting spatial invariance with low-rank local connectivity, in ICML 2020.

[5] Decoupled Dynamic Filter Networks, in CVPR 2021.

[6] A ConvNet for the 2020s, in arXiv 2022.

[7] Learning spatiotemporal features with 3d convolutional networks, in ICCV 2015.

[8] Slowfast networks for video recognition, in ICCV 2019.

内容中包含的图片若涉及版权问题，请及时与我们联系删除