导言：本期给大家分享NetworkX官方给出的社交网络分析案例：Facebook网络分析[1]，以进一步加深对复杂网络基础知识的理解。
这个笔记本包含了一个社交网络分析，主要是用NetworkX的库执行的。具体来说，将对10个人的facebook圈子(好友列表)进行检查和审查，以提取各种有价值的信息。数据集可以在斯坦福大学的网站上[2]找到。此外，众所周知，facebook网络是无向的，没有权重，因为一个用户可能只与另一个用户成为一次好友。从图表分析的角度来看数据集：
★ 每个节点代表一个匿名的facebook用户，他属于这十个好友列表中的一个。
★ 每条边都对应着属于这个网络的两个facebook用户的友谊。换句话说，两个用户必须在facebook上成为好友才能在特定的网络中连接。
下面给出官方的jupyter notebook示例代码：
首先，导入必要的库：
import pandas as pd
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from random import randint
从数据文件夹加载连边数据，每条边都是一个新行，每条边都有一个start_node和一个end_node列：
facebook = pd.read_csv(
    "data/facebook_combined.txt.gz",
    compression="gzip",
    sep=" ",
    names=["start_node", "end_node"],
)

 

创建网络：
G = nx.from_pandas_edgelist(facebook, "start_node", "end_node")
可视化网络：因为我们对数据的结构没有任何真正的感觉，所以让我们从使用random_layout查看网络，这是最快的布局函数之一。
fig, ax = plt.subplots(figsize=(15, 9))
ax.axis("off")
plot_options = {"node_size": 10, "with_labels": False, "width": 0.15}
nx.draw_networkx(G, pos=nx.random_layout(G), ax=ax, **plot_options)
生成的图不是很有用，这种图可视化有时被通俗地称为“毛球”，因为重叠的边会导致纠缠的混乱。
很明显，如果我们想要获得数据的感觉，我们需要在定位上施加更多的结构。为此，我们可以使用spring_layout函数，它是networkx绘图模块的默认布局函数。spring_layout函数的优点是它考虑了节点和边来计算节点的位置。然而，缺点是这个过程的计算成本要高得多，而且对于有100个节点和1000个边的图来说会非常慢。
由于我们的数据集有超过80k条边，我们将限制spring_layout函数中使用的迭代次数，以减少计算时间。我们还将保存计算出来的布局，以便在将来的可视化中使用它。
pos = nx.spring_layout(G, iterations=15, seed=1721)
fig, ax = plt.subplots(figsize=(15, 9))
ax.axis("off")
nx.draw_networkx(G, pos=pos, ax=ax, **plot_options)
★ 获取网络的基本拓扑属性：
# 节点数量
G.number_of_nodes()
4039
# 连边数量
G.number_of_edges()
88234
np.mean([d for _, d in G.degree()])
43.69101262688784
shortest_path_lengths = dict(nx.all_pairs_shortest_path_length(G))
# Length of shortest path between nodes 0 and 42
shortest_path_lengths[0][42]  
1
diameter = max(nx.eccentricity(G, sp=shortest_path_lengths).values())
diameter
8
# Compute the average shortest path length for each node
average_path_lengths = [
    np.mean(list(spl.values())) for spl in shortest_path_lengths.values()
]
# The average over all nodes
np.mean(average_path_lengths)
3.691592636562027
上述结果代表了所有节点对最短路径长度的平均值：为了从一个节点到达另一个节点，平均大约要遍历3.6条边。
上面的度量捕获了关于网络的有用信息，但是像平均值这样的度量只代表了分布的一个时刻。我们可以通过预先计算的dict-of-dicts构建一个最短路径长度分布的可视化：
# We know the maximum shortest path length (the diameter), so create an array
# to store values from 0 up to (and including) diameter
path_lengths = np.zeros(diameter + 1, dtype=int)

# Extract the frequency of shortest path lengths between two nodes
for pls in shortest_path_lengths.values():
    pl, cnts = np.unique(list(pls.values()), return_counts=True)
    path_lengths[pl] += cnts

# Express frequency distribution as a percentage (ignoring path lengths of 0)
freq_percent = 100 * path_lengths[1:] / path_lengths[1:].sum()

# Plot the frequency distribution (ignoring path lengths of 0) as a percentage
fig, ax = plt.subplots(figsize=(15, 8))
ax.bar(np.arange(1, diameter + 1), height=freq_percent)
ax.set_title(
    "Distribution of shortest path length in G", fontdict={"size": 35}, loc="center"
)
ax.set_xlabel("Shortest Path Length", fontdict={"size": 22})
ax.set_ylabel("Frequency (%)", fontdict={"size": 22})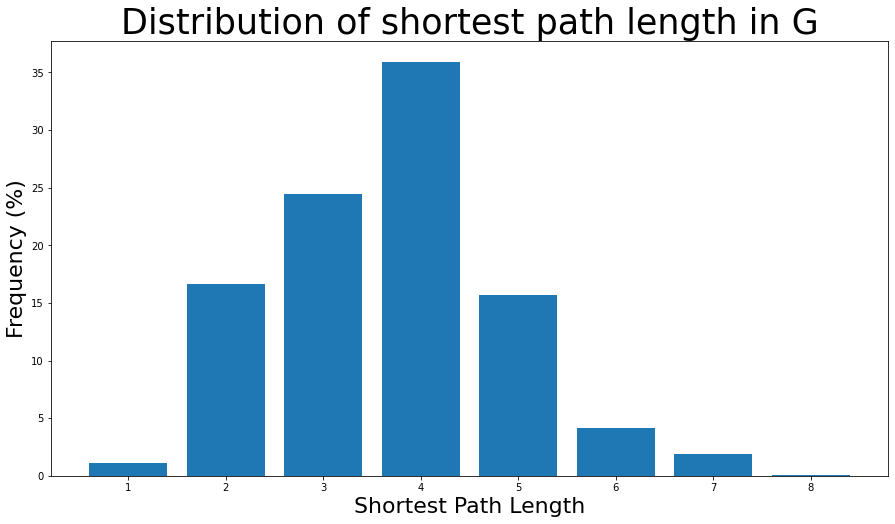
大多数最短路径的长度是从2条边到5条边的长度。此外，对于一对节点来说，其最短路径长度为8(直径长度)的可能性非常小，因为其可能性小于0.1%。
计算图的密度，显然，这是一个非常稀疏的图。以及图包含组件的数量，正如预期的那样，这个网络由一个巨大的组件组成：
nx.density(G)
0.010819963503439287
nx.number_connected_components(G)
1
接下来，对facebook网络的中心性指标进行研究：
★ 度中心性：度中心性简单地根据每个节点所拥有的链接数量分配一个重要分数。在这个分析中，这意味着一个节点的中心性程度越高，连接到该节点的边越多，因此该节点的邻居节点(facebook好友)也越多。事实上，一个节点的中心性程度就是它所连接的节点的分数。换句话说，它是网络中特定节点与交友关系的百分比。
首先，我们找到中心度最高的节点。其中，8个度中心性最高的节点及其度中心性如下图所示：
degree_centrality = nx.centrality.degree_centrality(G)  
# save results in a variable to use again
(sorted(degree_centrality.items(), key=lambda item: item[1], reverse=True))[:8]

[(107, 0.258791480931154),
 (1684, 0.1961367013372957),
 (1912, 0.18697374938088163),
 (3437, 0.13546310054482416),
 (0, 0.08593363051015354),
 (2543, 0.07280832095096582),
 (2347, 0.07206537890044576),
 (1888, 0.0629024269440317)]
现在我们还可以看到中心度最高的节点的邻居数量：
(sorted(G.degree, key=lambda item: item[1], reverse=True))[:8]
[(107, 1045),
 (1684, 792),
 (1912, 755),
 (3437, 547),
 (0, 347),
 (2543, 294),
 (2347, 291),
 (1888, 254)]
绘制出程度中心性的分布：
plt.figure(figsize=(15, 8))
plt.hist(degree_centrality.values(), bins=25)
plt.xticks(ticks=[0, 0.025, 0.05, 0.1, 0.15, 0.2])  # set the x axis ticks
plt.title("Degree Centrality Histogram ", fontdict={"size": 35}, loc="center")
plt.xlabel("Degree Centrality", fontdict={"size": 20})
plt.ylabel("Counts", fontdict={"size": 20})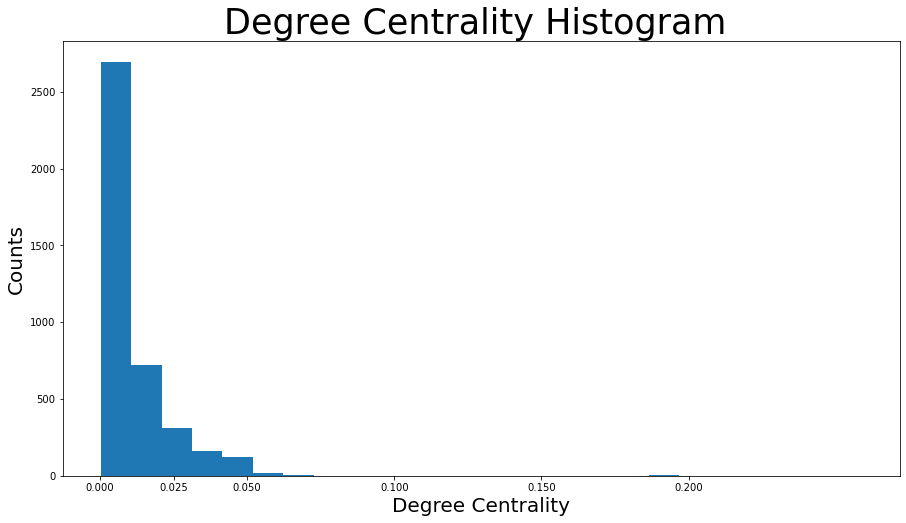
现在让我们根据节点的大小来检查中心度最高的用户：
node_size = [
    v * 1000 for v in degree_centrality.values()
]  # set up nodes size for a nice graph representation
plt.figure(figsize=(15, 8))
nx.draw_networkx(G, pos=pos, node_size=node_size, with_labels=False, width=0.15)
plt.axis("off")
★ 介数中心性：
betweenness_centrality = nx.centrality.betweenness_centrality(
    G
)  # save results in a variable to use again
(sorted(betweenness_centrality.items(), key=lambda item: item[1], reverse=True))[:8]

[(107, 0.4805180785560152),
 (1684, 0.3377974497301992),
 (3437, 0.23611535735892905),
 (1912, 0.2292953395868782),
 (1085, 0.14901509211665306),
 (0, 0.14630592147442917),
 (698, 0.11533045020560802), (567, 0.09631033121856215)]
plt.figure(figsize=(15, 8))
plt.hist(betweenness_centrality.values(), bins=100)
plt.xticks(ticks=[0, 0.02, 0.1, 0.2, 0.3, 0.4, 0.5])  # set the x axis ticks
plt.title("Betweenness Centrality Histogram ", fontdict={"size": 35}, loc="center")
plt.xlabel("Betweenness Centrality", fontdict={"size": 20})
plt.ylabel("Counts", fontdict={"size": 20})
按照介数值的大小进行网络可视化：
node_size = [
    v * 1200 for v in betweenness_centrality.values()
]  # set up nodes size for a nice graph representation
plt.figure(figsize=(15, 8))
nx.draw_networkx(G, pos=pos, node_size=node_size, with_labels=False, width=0.15)
plt.axis("off")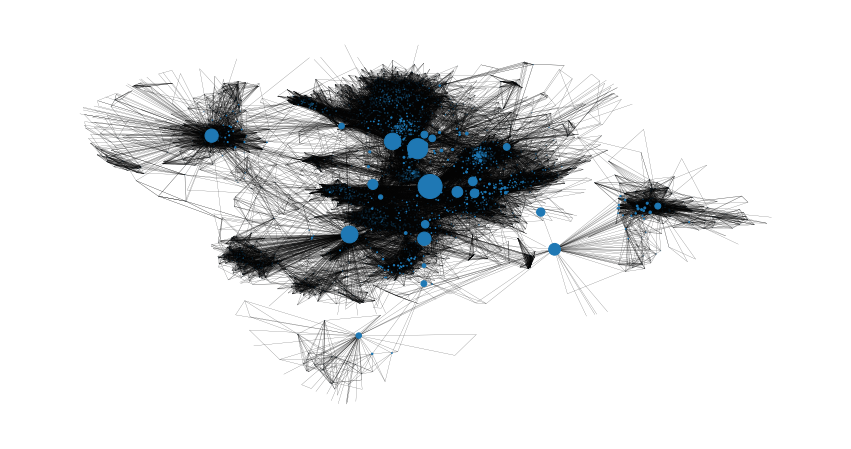
★ 接近度中心性：
closeness_centrality = nx.centrality.closeness_centrality(
    G
)  # save results in a variable to use again
(sorted(closeness_centrality.items(), key=lambda item: item[1], reverse=True))[:8]

[(107, 0.45969945355191255),
 (58, 0.3974018305284913),
 (428, 0.3948371956585509),
 (563, 0.3939127889961955),
 (1684, 0.39360561458231796),
 (171, 0.37049270575282134),
 (348, 0.36991572004397216),
 (483, 0.3698479575013739)]
# 此外，一个特定节点v到任何其他节点的平均距离也可以很容易地用公式求出：1 / closeness_centrality[107]
2.1753343239227343
plt.figure(figsize=(15, 8))
plt.hist(closeness_centrality.values(), bins=60)
plt.title("Closeness Centrality Histogram ", fontdict={"size": 35}, loc="center")
plt.xlabel("Closeness Centrality", fontdict={"size": 20})
plt.ylabel("Counts", fontdict={"size": 20})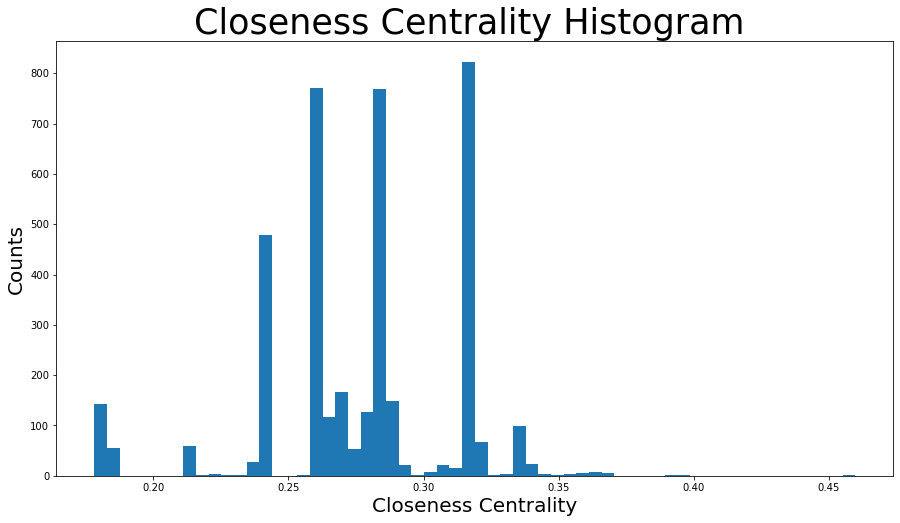
node_size = [
    v * 50 for v in closeness_centrality.values()
]  # set up nodes size for a nice graph representation
plt.figure(figsize=(15, 8))
nx.draw_networkx(G, pos=pos, node_size=node_size, with_labels=False, width=0.15)
plt.axis("off")

以及特征向量中心性等中心性指标，用类似的方式即

可获取上述图表。

 
★ 集聚系数：
# 平均集聚系数
nx.average_clustering(G)
0.6055467186200876

plt.figure(figsize=(15, 8))
plt.hist(nx.clustering(G).values(), bins=50)
plt.title("Clustering Coefficient Histogram ", fontdict={"size": 35}, loc="center")
plt.xlabel("Clustering Coefficient", fontdict={"size": 20})
plzt.ylabel("Counts", fontdict={"size": 20})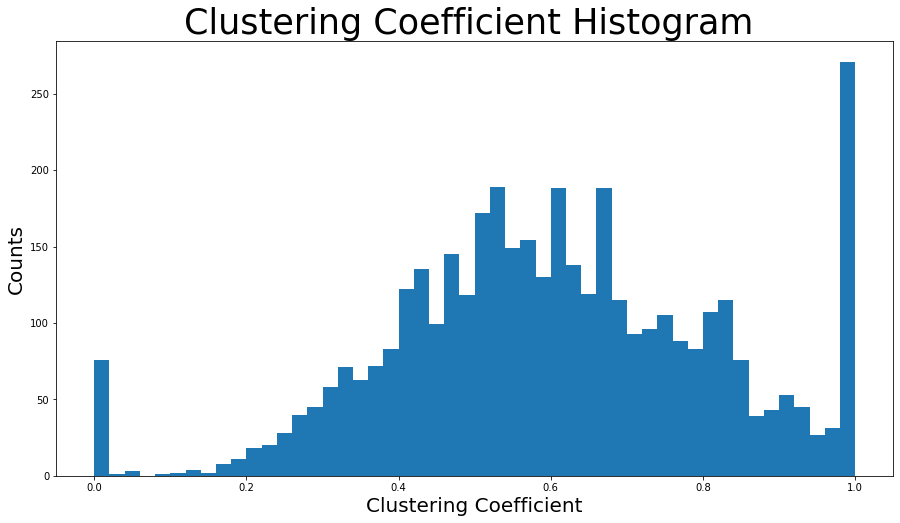
★ 桥：
nx.has_bridges(G)
True

# 输出桥的数量
bridges = list(nx.bridges(G))
len(bridges)
75
plt.figure(figsize=(15, 8))
nx.draw_networkx(G, pos=pos, node_size=10, with_labels=False, width=0.15)
nx.draw_networkx_edges(
    G, pos, edgelist=local_bridges, width=0.5, edge_color="lawngreen"
)  # green color for local bridges
nx.draw_networkx_edges(
    G, pos, edgelist=bridges, width=0.5, edge_color="r"
)  # red color for bridges
plt.axis("off")
★ 网络关联系数：
nx.degree_assortativity_coefficient(G)
0.06357722918564943
nx.degree_pearson_correlation_coefficient(G)  
0.06357722918564918
★ 网络社区：社区是一组节点，因此组内的节点连接
的边要比组间连接的边多得多。该网络将采用两种不
同的算法进行社区检测。
首先，采用半同步标签传播方法检测社区：

该函数自行确定将检测到的社区数量。现在将遍历社
区，并创建一个颜色列表，为属于同一个社区的节点
包含相同的颜色。此外，社区的数量也被打印出来:
colors = ["" for x in range(G.number_of_nodes())]  # initialize colors list
counter = 0
for com in nx.community.label_propagation_communities(G):
    color = "#%06X" % randint(0, 0xFFFFFF)  # creates random RGB color
    counter += 1
    for node in list(
        com
    ):  # fill colors list with the particular color for the community nodes
        colors[node] = color
counter
44
plt.figure(figsize=(15, 9))
plt.axis("off")
nx.draw_networkx(
    G, pos=pos, node_size=10, with_labels=False, width=0.15, node_color=colors
)

其次，采用异步流体团体算法：
colors = ["" for x in range(G.number_of_nodes())]
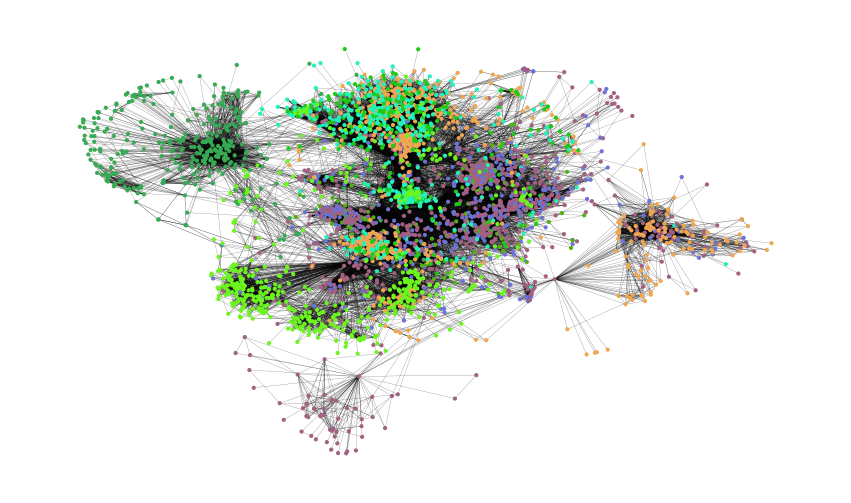
for com in nx.community.asyn_fluidc(G, 8, seed=0):
    color = "#%06X" % randint(0, 0xFFFFFF)  # creates random RGB color
    for node in list(com):
        colors[node] = color

plt.figure(figsize=(15, 9))
plt.axis("off")
nx.draw_networkx(
    G, pos=pos, node_size=10, with_labels=False, width=0.15, node_color=colors
)

 

[1]https://networkx.org/nx-guides/content/exploratory_notebooks/facebook_notebook.html#id2
[2]http://snap.stanford.edu/data/ego-Facebook.html

内容中包含的图片若涉及版权问题，请及时与我们联系删除