编者按:“几何深度学习”先驱、牛津大学DeepMind教授Michael Bronstein 最近在博客发表系列长文《迈向几何深度学习》的第1篇:站在巨人的肩膀上。下文是对它的编译。
几何深度学习从对称性和不变性的角度来处理广泛的 ML 问题,为 CNN、GNN 和 Transformers 等神经网络架构提供了通用的蓝图。我们在一系列新发表的文章里,研究了从古希腊几何到图神经网络的历史中,这些想法是如何出现的。

图片基于Shutterstock网站
雪花和标准模型有什么共同点?对称。在“迈向几何深度学习”系列的第一篇文章中,我们将讨论对称性的概念如何帮助组织十九世纪动物园的几何结构并彻底改变理论物理学。这篇文章基于M. M. Bronstein,J. Bruna,T. Cohen和P. Veličković 合著的《Geometric Deep Learning》(完稿后将由麻省理工学院出版社出版)书的介绍章节,以及我们开设的非洲机器智能硕士(AMMI)课程内容。请参阅我们已经总结的关于几何深度学习概念的文章。
过去的十年,以深度学习为代表,我们已经见证了数据科学和机器学习的实验性革命。许多曾被认为遥不可及的高维学习任务——计算机视觉、围棋或蛋白质折叠——实际上在适当的计算规模下是可行的。值得注意的是,深度学习本质是从两个简单的算法原则中构建的:首先,表示特征学习的概念,由此开展的,通常是分层、特征捕获每个任务的适当规律性概念;其次,通过梯度下降优化来学习,通常用反向传播实现。
虽然学习高维的泛型函数是一个被诅咒的估计问题,但我们感兴趣的大多数任务都不是泛型的,并具有物理世界潜在低维性和结构引起的基本预定义规则。几何深度学习关注的是通过统一的几何原理来揭示这些规律性,这些原理可以被广泛应用。
利用大系统的已知对称性是对抗维度诅咒的强大而经典的补救措施,并构成了大多数物理理论的基础。深度学习系统也不例外,从早期开始,研究人员就通过调正神经网络,以便利用物理测量产生的低维几何,例如图像中的网格、时间序列中的序列或分子中的位置和动量,以及它们相关的对称性,例如平移或旋转。
由于这些想法在科学研究中根深蒂固,我们将尝试着看看它们在整个历史中是如何演变,并最终形成一个普适于各神经网络架构的共同蓝图。
秩序、美丽和完美
“对称性,无论你对它的定义有多么宽泛或者狭窄,它均是人类历代以来试图理解和创造秩序、美丽和完美的一个构思”——赫尔曼·韦尔(Hermann Weyl,1952)
这个颇有诗意的对称性定义,来自于伟大的数学家赫尔曼·外尔(Hermann Weyl)的同名著作[1],这部“天鹅之歌”般作品出版于他在普林斯顿高等研究院的退休前夕。外尔将对称性在科学和艺术中占据的特殊地位追溯到古代,从苏美尔对称设计到毕达哥拉斯主义者——毕达哥拉斯主义者认为圆由于其旋转对称性而完美。柏拉图认为,今天以他名字命名的五个规则多面体是如此基本,以至于它们一定是塑造物质世界的基本组成部分。
然而,尽管柏拉图创造了术语συμμετρία,字面意思是“相同的措施”,但他只是模糊地用它来传达艺术中比例和音乐中的和谐之美。德国天文学家和数学家约翰内斯·开普勒(Johannes Kepler)首次对水晶体的对称形状进行了严格的分析。在他的专著《论六角雪花上》(On the Six-Cornered Snowflake)[2]中,他将雪花的六倍二面体结构归因于粒子的六角密排——这一观点,虽然在我们形成对物质构成的清晰理解之前就存在,但今天仍然作为了晶体学的基础[3]。

柏拉图(左)认为对称多面体(“柏拉图固体”)是自然界的基本组成部分。约翰内斯·开普勒(右)首次将水晶体的六重对称性归因于粒子的六边形堆积,早于现代晶体学。
在现代数学中,对称性几乎是用群论的语言形式一致地表达出来。这一理论的起源通常归功于Évariste Galois,他创造了这个术语,并在1830年代用它来研究多项式方程的可解性[4]。另外两个与群论相关的名字是Sophus Lie和Felix Klein,他们曾经会面并一起富有成效地进行了合作[5]。前者发展出了连续对称理论,今天以他的名字命名(李群);后者在他的埃尔兰根纲领中宣称群论是几何学的组织原理。鉴于Klein的纲领是几何深度学习的灵感来源,因此值得花更多时间研究其历史背景和革命性影响。

埃瓦里斯特·伽罗瓦(左)和他在致命决斗前一天晚上给朋友的信,描述了群论。Felix Klein(右)和为他的教授任命准备的研究招生简章的封面,该研究招生简章已作为“埃尔兰根计划”进入了数学史。克莱因的肖像:伊霍尔·戈尔斯基。
一个陌生的新世界
近2300年前,古希腊的欧几里得在一篇名为《元素》的专著中正式确定了现代几何学的基础。欧几里得几何(在学校仍通称为“几何”)是一组建立在五个直观公理或假设基础上的体系。第五个假设指出过一条给定直线外一点,有且只有一条直线与已知直线平行——公理特质似乎不那么明显,但自古以来无数杰出的数学家们咬牙切齿地试图证明它,均无功而返。
解决平行问题的早期方法出现在十一世纪的波斯专著“关于欧几里得元素假设的困难的评论”中,作者是Omar Khayyam[6]。十八世纪的意大利耶稣会牧师乔瓦尼·萨切里(Giovanni Saccheri)可能知道这部先前的作品——从他自己的作品《欧几里得》的标题来看:Euclides ab omni nævo vindicatus(“欧几里得清除了所有污点”)。
和Khayyam方案类似,乔瓦尼·萨切里考虑了四边形的顶角,其侧面垂直于底部。锐角导致无限多的非相交线,这些线可以通过一个不在直线上的点,这一结论似乎非常违反直觉,以至于他定论为“repugnatis naturæ linæ rectæ(与直线的性质相悖)”[7]。
 乔瓦尼·萨切里的“Euclides vindicatus”的卷首部分,以及将双曲几何判断为“repugnatis naturæ linæ rectæ”的段落。
乔瓦尼·萨切里的“Euclides vindicatus”的卷首部分,以及将双曲几何判断为“repugnatis naturæ linæ rectæ”的段落。
十九世纪时人们已经意识到第五假设并不是必需的,可以基于不同的平行概念构建可替代的几何。一个早期的例子是投影几何,顾名思义,它出现在透视绘图和建筑中。在这种类型的几何中,点和线是可以互换的,并且没有通常意义上的平行线:任何线都会在“无穷远处的点”相遇。虽然投影几何的现象自古以来就已为人所知,但首位系统地对它进行研究的,是1812年的让-维克多·庞塞莱特(Jean-Victor Poncelet)[8]。
关于非欧几何的第一次构造目前尚存争议。卡尔·弗里德里希·高斯(Carl Friedrich Gauss)在1813年左右研究过它,但从未发表过任何结果[9]。非欧几何主题的第一本出版物是俄罗斯数学家尼古拉·罗巴切夫斯基(Nikolai Lobachevsky)的《论几何的起源》(On the Origins of Geometry)[10]。在这项工作中,他认为第五假设是一个任意的限制,并提出了一个替代方案,即多条线可以穿过一个与给定点平行的点。这种构造需要一个具有负曲率的空间 - 我们现在称之为双曲空间 - 这个概念在当时还未被大家完全掌握[11]。

1823 年 11 月 3 日,亚诺什·博雅伊用匈牙利语写给父亲的信(左),宣布他发现了双曲几何。尼古拉·罗巴切夫斯基(右)和他的作品《论几何学的起源》的第一页,出版于1829年。
罗巴切夫斯基的想法似乎是异端邪说,他被同事们公开嘲笑[12]。匈牙利的János Bolyai独立地发现了类似的结构,他于1832年以“绝对几何”的名义发表了它。较早在1823年给他父亲的一封信中,他热情地写下了这一新发展:
“我发现了如此美妙的事情,我感到惊讶......凭空,我创造了一个陌生的新世界“——János Bolyai(1823)
与此同时,新的几何形状继续像聚宝盆一样出现。奥古斯特·莫比乌斯[13],因对仿射几何的研究声誉鹊起。高斯的学生伯恩哈特·黎曼(Bernhardt Riemann)在他的资格认证讲座中介绍了一类非常广泛的几何学——今天获誉为黎曼几何——随后以“Über die Hypothesen, welche der Geometrie zu Grunde liegen”(“关于几何学所基于的假设”)的标题发表[14]。黎曼几何的一个特例是球体的“椭圆”几何,这是违反欧几里得第五假设的另一种构造,因为球体上没有一个点可以画出一条从不与给定线相交的线。
到了十九世纪下半叶,欧几里得对几何学的垄断被完全关闭。新型几何(欧几里得,仿射,射影,双曲,球面)出现了并成为独立的研究领域。但是,这些几何形状及其层次结构之间的关系尚不清楚。
正是在这种令人兴奋但又混乱的情况下,Felix Klein出现了,他以天才的洞察力,使用群论作为对称性的代数抽象来组织“几何动物园”。克莱因在埃尔兰根被任命为教授时只有23岁,按照德国大学的惯例,他被要求提供首个研究计划 - 名为Vergleichende Betrachtungen über neuere geometrische Forschungen(“对最近几何研究的比较回顾”),它已作为“埃尔兰根计划”进入数学史册[15]。
克莱因的突破性见解是将几何学定义为对不变量的研究,换句话说,是在某种类型的变换(对称性)下保留的结构。克莱因使用群论的形式主义来定义这种变换,并使用群及其子群的层次结构来对由它们产生的不同几何进行分类。
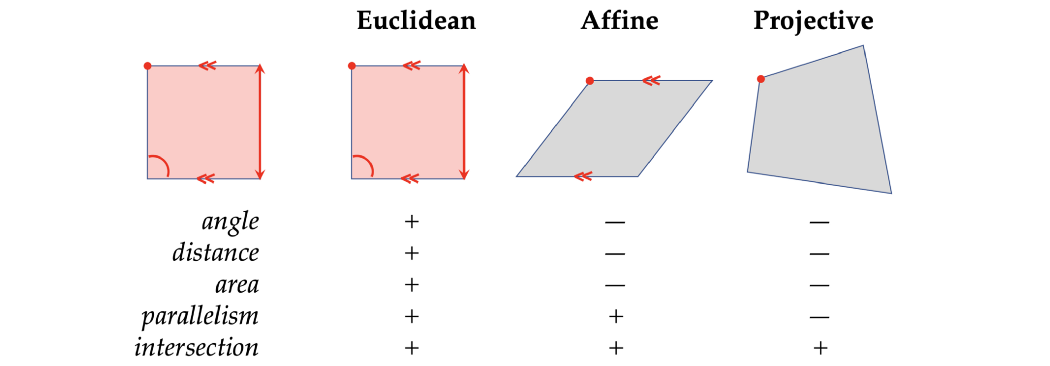
莱因的埃尔兰根计划将几何定义为一组变换的空间。这允许对不同类型的几何图形进行分类。
看起来,欧几里得几何是仿射几何的一个特例,而仿射几何又是射影几何的一个特例(或者就群论而言,欧几里得群是射影群的子群)。从某种意义上说,克莱因的埃尔兰根纲领是几何学的“第二代数化”(第一个是勒内·笛卡尔的解析几何,和带有他的拉丁名称笛卡尔的坐标方法),它允许产生过去几何学中无法产生的结果。
更具概括性的黎曼几何被明确排除在克莱因的统一几何图景之外,它又花了五十年的时间才被整合,这在很大程度上要归功于埃莉·卡坦在1920年代的工作。此外,范畴论,现在在纯数学中普遍存在,可以“被视为克莱因·埃尔兰根纲领的延续,从某种意义上说,一个几何空间及其一组变换被推广到一个具有映射代数的范畴”,用它的创造者塞缪尔·艾伦伯格和桑德斯·麦克莱恩的话说[16]。
万物理论
Klein在他的Vergleichende Betrachtungen [17]中抱怨说:
“数学物理学家是多么执着地无视许多情况下只需适度培养投影观点而带来的优势。”——Felix Klein(1872)
他倡导在物理学中利用几何学和对称性原理,这预示了这个领域在下一世纪中的真正革命性变化。在哥廷根[18],克莱因的同事Emmy Noether[19]证明了物理系统行为中的每个可微对称性都有相应的守恒定律[20]。无论如何,这是一个惊人的结果:事先,需要细致的实验观察来发现能量守恒定律等基本定律,即使这样,它也不是来自任何地方的经验结果。诺特定理——用诺贝尔奖获得者弗兰克·维尔切克(Frank Wilczek)的话来说,“20世纪和21世纪物理学的指路明灯”——例如,它允许证明能量守恒来自时间的平移对称性,这是一个相当直观的想法,即实验的结果不应该取决于它是今天还是明天进行。

赫尔曼·外尔(左)和爱因斯坦1918年的明信片(与外尔最初提出的规范理论进行辩论)。艾米·诺特(右)和同年的出版物,包含以她命名的定理。诺特的肖像:伊霍尔·戈尔斯基。
另一个与电荷守恒相关的对称性,即电磁场的全局规范不变性,首先出现在麦克斯韦的电动力学公式中[21];然而,它的重要性最初并未引起注意。赫尔曼·外尔(Hermann Weyl)在20世纪初首次在物理学中引入了规范不变性的概念[22],他强调了它作为可以推导出电磁学的原理的作用。直到这个基本原理——由杨和米尔斯[23]开发的广义形式——被证明成功地提供了一个统一的框架来描述电磁学的量子力学行为以及弱力和强力,最终在标准模型中达到了顶峰,该模型捕获了除重力之外的所有自然界基本力。正如另一位诺贝尔奖得主菲利普·安德森(Philip Anderson)[24]简明扼要地指出的那样:
“说物理学是关于对称性的研究,仅仅是略微夸大其词而已。”——菲利普·安德森(Philip Anderson,1972)
说到这里,一个不耐烦的读者可能会感到困惑:所有这些对几何和物理学历史的探索,无论多么令人兴奋,都与深度学习有什么关系?这正如我们将在下一部分中看到的,即使在早期探索“模式识别”时,对称性和不变性的几何概念也被认为是至关重要的,公平地说,几何学从一开始就伴随着人工智能的新生领域。
参考资料
[1] H. Weyl, Symmetry (1952), Princeton University Press.
[2] Fully titled Strena, Seu De Nive Sexangula (’New Year’s gift, or on the Six-Cornered Snowflake’) was, as suggested by the title, a small booklet sent by Kepler in 1611 as a Christmas gift to his patron and friend Johannes Matthäus Wackher von Wackenfels.
[3] P. Ball, In retrospect: On the six-cornered snowflake (2011), Nature 480 (7378):455–455.
[4] Galois famously described the ideas of group theory (which he considered in the context of finding solutions to polynomial equations) and coined the term “group” (groupe in French) in a letter to a friend written on the eve of his fatal duel. He asked to communicate his ideas to prominent mathematicians of the time, expressing the hope that they would be able to “‘decipher all this mess’” (“‘déchiffrer tout ce gâchis”). Galois died two days later from wounds suffered in the duel aged only 20, but his work has been transformational in mathematics.
[5] See biographic notes in R. Tobies, Felix Klein — Mathematician, Academic Organizer, Educational Reformer (2019), The Legacy of Felix Klein 5–21, Springer.
[6] Omar Khayyam is nowadays mainly remembered as a poet and author of the immortal line “‘a flask of wine, a book of verse, and thou beside me.”
[7] The publication of Euclides vindicatus required the approval of the Inquisition, which came in 1733 just a few months before the author’s death. Rediscovered by the Italian differential geometer Eugenio Beltrami in the nineteenth century, Saccheri’s work is now considered an early almost-successful attempt to construct hyperbolic geometry.
[8] Poncelet was a military engineer and participant in Napoleon’s Russian campaign, where he was captured and held as a prisoner until the end of the war. It was during this captivity period that he wrote the Traité des propriétés
projectives des figures (‘Treatise on the projective properties of figures,’ 1822) that revived the interest in projective geometry. Earlier foundation work on this subject was done by his compatriot Gérard Desargues in 1643.
[9] In the 1832 letter to Farkas Bolyai following the publication of his son’s results, Gauss famously wrote: “To praise it would amount to praising myself. For the entire content of the work coincides almost exactly with my own meditations which have occupied my mind for the past thirty or thirty-five years.” Gauss was also the first to use the term ‘non-Euclidean geometry,’ referring strictu sensu to his own construction of hyperbolic geometry. See
R. L. Faber, Foundations of Euclidean and non-Euclidean geometry (1983), Dekker and the blog post in Cantor’s Paradise.
[10] Н. И. Лобачевский, О началах геометрии (1829).
[11] A model for hyperbolic geometry known as the pseudosphere, a surface with constant negative curvature, was shown by Eugenio Beltrami, who also proved that hyperbolic geometry was logically consistent. The term ‘hyperbolic geometry’ was introduced by Felix Klein.
[12] For example, an 1834 pamphlet signed only with the initials “S.S.” (believed by some to belong to Lobachevsky’s long-time opponent Ostrogradsky) claimed that Lobachevsky made “an obscure and heavy theory” out of “the lightest and clearest chapter of mathematics, geometry,” wondered why one would print such “ridiculous fantasies,” and suggested that the book was a “joke or satire.”
[13] A. F. Möbius, Der barycentrische Calcul (1827).
[14] B. Riemann, Über die Hypothesen, welche der Geometrie zu Grunde liegen (1854). See English translation.
[15] According to a popular belief, repeated in many sources including Wikipedia, the Erlangen Programme was delivered in Klein’s inaugural address in October 1872. Klein indeed gave such a talk (though on December 7, 1872), but it was for a non-mathematical audience and concerned primarily his ideas of mathematical education; see[4]. The name “Programme” comes from the subtitle of the published brochure [17], Programm zum Eintritt in die philosophische Fakultät und den Senat der k. Friedrich-Alexanders-Universität zu Erlangen (‘Programme for entry into the Philosophical Faculty and the Senate of the Emperor Friedrich-Alexander University of Erlangen’).
[16] S. Eilenberg and S. MacLane, General theory of natural equivalences (1945), Trans. AMS 58(2):231–294. See also J.-P. Marquis, Category Theory and Klein’s Erlangen Program (2009), From a Geometrical Point of View 9–40, Springer.
[17] F. Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen (1872). See English translation.
[18] At the time, Göttingen was Germany’s and the world’s leading centre of mathematics. Though Erlangen is proud of its association with Klein, he stayed there for only three years, moving in 1875 to the Technical University of Munich (then called Technische Hochschule), followed by Leipzig (1880), and finally settling down in Göttingen from 1886 until his retirement.
[19] Emmy Noether is rightfully regarded as one of the most important women in mathematics and one of the greatest mathematicians of the twentieth century. She was unlucky to be born and live in an epoch when the academic world was still entrenched in the medieval beliefs of the unsuitability of women for science. Her career as one of the few women in mathematics having to overcome prejudice and contempt was a truly trailblazing one. It should be said to the credit of her male colleagues that some of them tried to break the rules. When Klein and David Hilbert first unsuccessfully attempted to secure a teaching position for Noether at Göttingen, they met fierce opposition from the academic hierarchs. Hilbert reportedly retorted sarcastically to concerns brought up in one such discussion: “I do not see that the sex of the candidate is an argument against her admission as a Privatdozent. After all, the Senate is not a bathhouse”(see C. Reid, Courant in Göttingen and New York: The Story of an Improbable Mathematician (1976), Springer). Nevertheless, Noether enjoyed great esteem among her close collaborators and students, and her male peers in Göttingen affectionately referred to her as “Der Noether,” in the masculine (see C. Quigg, Colloquium: A Century of Noether’s Theorem (2019), arXiv:1902.01989).
[20] E. Noether, Invariante Variationsprobleme (1918), König Gesellsch. d. Wiss. zu Göttingen, Math-Phys. 235–257. See English translation.
[21] J. C. Maxwell, A dynamical theory of the electromagnetic field (1865), Philosophical Transactions of the Royal Society of London 155:459–512.
[22] Weyl first conjectured (incorrectly) in 1919 that invariance under the change of scale or “gauge” was a local symmetry of electromagnetism. The term gauge, or Eich in German, was chosen by analogy to the various track gauges of railroads. After the development of quantum mechanics, he modified the gauge choice by replacing the scale factor with a change of wave phase in iH. Weyl, Elektron und gravitation (1929), Zeitschrift für Physik 56 (5–6): 330–352. See N. Straumann, Early history of gauge theories and weak interactions (1996), arXiv:hep-ph/9609230.
[23] C.-N. Yang and R. L. Mills, Conservation of isotopic spin and isotopic gauge invariance (1954), Physical Review 96 (1):191.
[24] P. W. Anderson, More is different (1972), Science 177 (4047): 393–396.
The portraits of Klein and Noether were hand-drawn by Ihor Gorskiy. Detailed lecture materials on Geometric Deep Learning are available on the project webpage. See Michael’s other posts in Towards Data Science, subscribe to his posts, get Medium membership, or follow Michael, Joan, Taco, and Petar on Twitter.
内容中包含的图片若涉及版权问题,请及时与我们联系删除










评论
沙发等你来抢