本文简要介绍ECCV 2022录用的论文“When Counting Meets HMER: Counting-Aware Network for Handwritten Mathematical Expression Recognition”的主要工作。该论文旨在缓解目前大部分基于注意力机制的手写数学公式识别算法在处理较长或者空间结构较复杂的数学公式时，容易出现的注意力不准确的情况。本文通过将符号计数任务和手写数学公式识别任务联合优化来增强模型对于符号位置的感知，并验证了联合优化和符号计数结果都对公式识别准确率的提升有贡献。相关代码已开源，地址见文末。

 

一、研究背景

OCR技术发展到今天，对于常规文本的识别已经达到了较高的准确率。但是对于在自动阅卷、数字图书馆建设、办公自动化等领域经常出现的手写数学公式，现有OCR算法的识准确率依然不太理想。不同于常规文本，手写数学公式有着复杂的空间结构以及多样化的书写风格，如图1所示。其中复杂的空间结构主要是由数学公式独特的分式、上下标、根号等结构造成的。虽然目前的OCR算法能较好地识别水平排布的常规文本，甚至对于一些多方向以及弯曲文本也能够有不错的识别效果，但是依然不能很好地识别具有复杂空间结构的数学公式。 

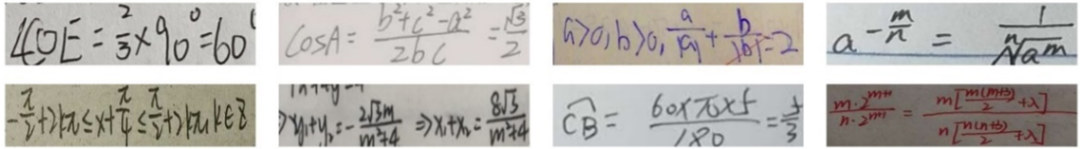
图1 手写数学公式示例

 

二、研究动机

现有的大部分手写数学公式识别算法采用的是基于注意力机制的编码器-解码器结构，模型在识别每一个符号时，需要注意到图像中该符号对应的位置区域。在识别常规文本时，注意力的移动规律比较单一，往往是从左至右或从右至左。但是在识别数学公式时，注意力在图像中的移动具有更多的可能性。因此，模型在解码较复杂的数学公式时，容易出现注意力不准确的现象，导致重复识别某符号或者是漏识别某符号。

为了缓解上述现象，本文提出将符号计数引入手写数学公式识别。这种做法主要基于以下两方面的考虑：1）符号计数（如图2(a)所示）可以隐式地提供符号位置信息，这种位置信息可以使得注意力更加准确（如图2(b)所示）。2）符号计数结果可以作为额外的全局信息来提升公式识别的准确率。 

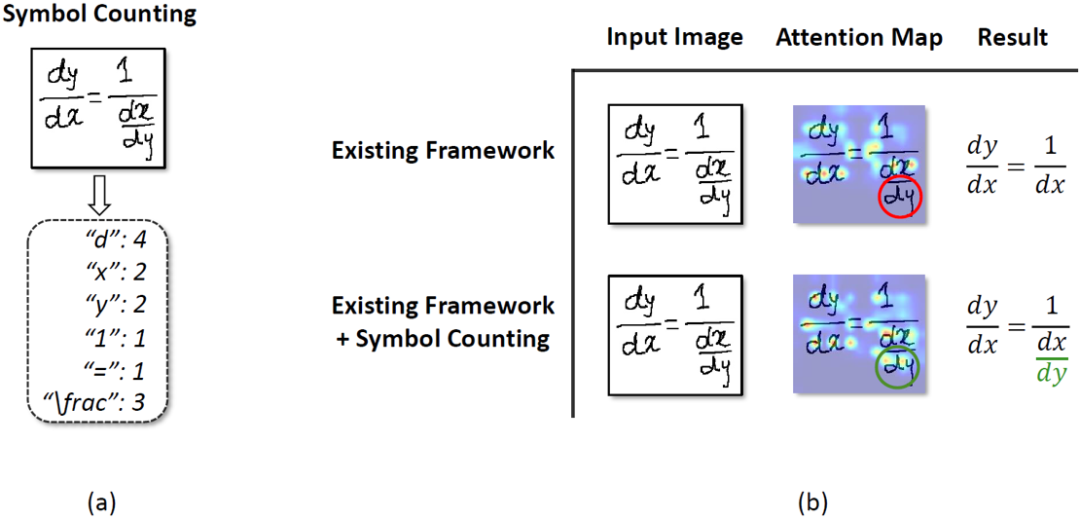
图2 （a）符号计数任务；（b）符号计数任务让模型拥有更准确的注意力

 

三、方法简述

模型整体框架：如图3所示，CAN模型由主干特征提取网络、多尺度计数模块（MSCM）和结合计数的注意力解码器（CCAD）构成。主干特征提取网络采用的是DenseNet[1]。对于给定的输入图像，主干特征提取网络提取出2D特征图F。随后该特征图F被输入到多尺度计数模块MSCM，输出计数向量V。特征图F和计数向量V都会被输入到结合计数的注意力解码器CCAD来产生最终的预测结果。 

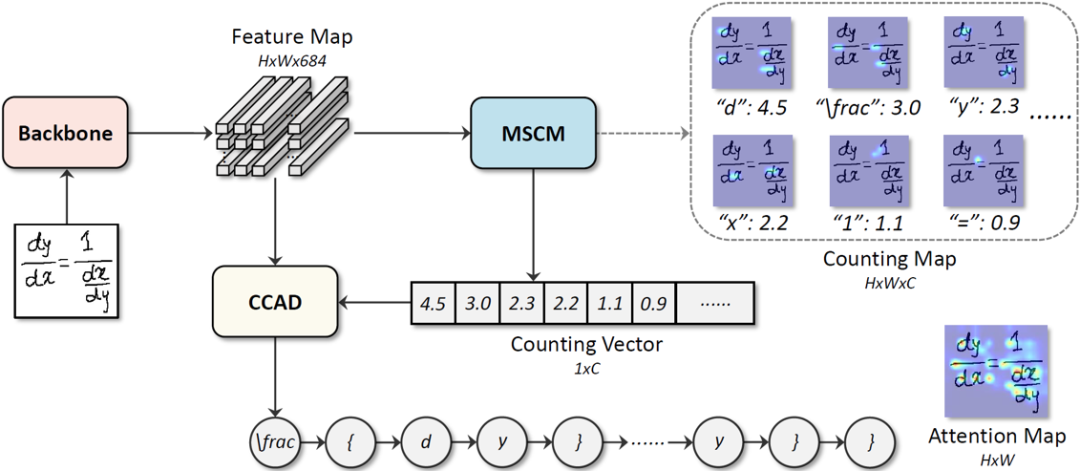
 图3 CAN模型整体框架

多尺度计数模块：在人群计数等任务中，部分方法采用弱监督的范式，在不需要使用人群位置标注的情况下预测人群密度图。本文借鉴了这一做法，在只使用公式识别原始标注（即LaTeX序列）而不使用符号位置标注的情况下进行多类符号计数。针对符号计数任务，该计数模块做了两方面独特的设计：1）用计数图的通道数表征类别数，并在得到计数图前使用Sigmoid激活函数将每个元素的值限制在(0,1)的范围内，这样在对计数图进行H和W维度上的加和后，可以直接表征各类符号的计数值。2）针对手写数学公式符号大小多变的特点，采用多尺度的方式提取特征以提高符号计数准确率。 

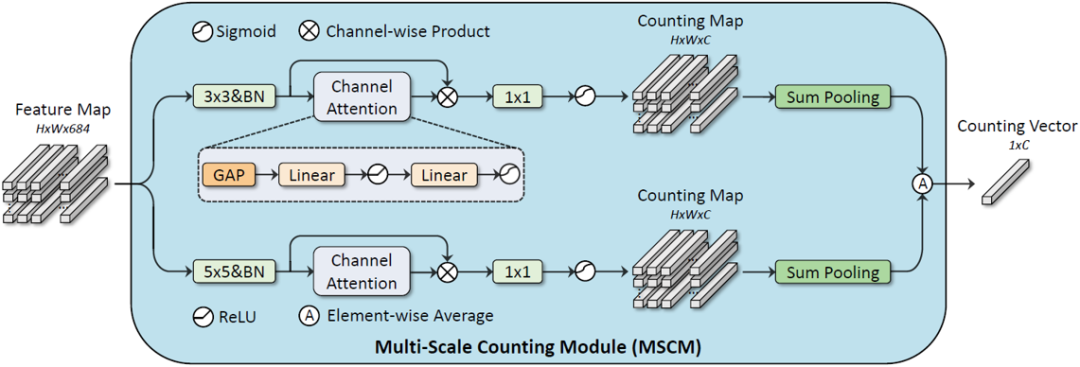
图4 多尺度计数模块MSCM

结合计数的注意力解码器：为了加强模型对于空间位置的感知，使用位置编码表征特征图中不同空间位置。另外，不同于之前大部分公式识别方法只使用局部特征进行符号预测的做法，在进行符号类别预测时引入符号计数结果作为额外的全局信息来提升识别准确率。 

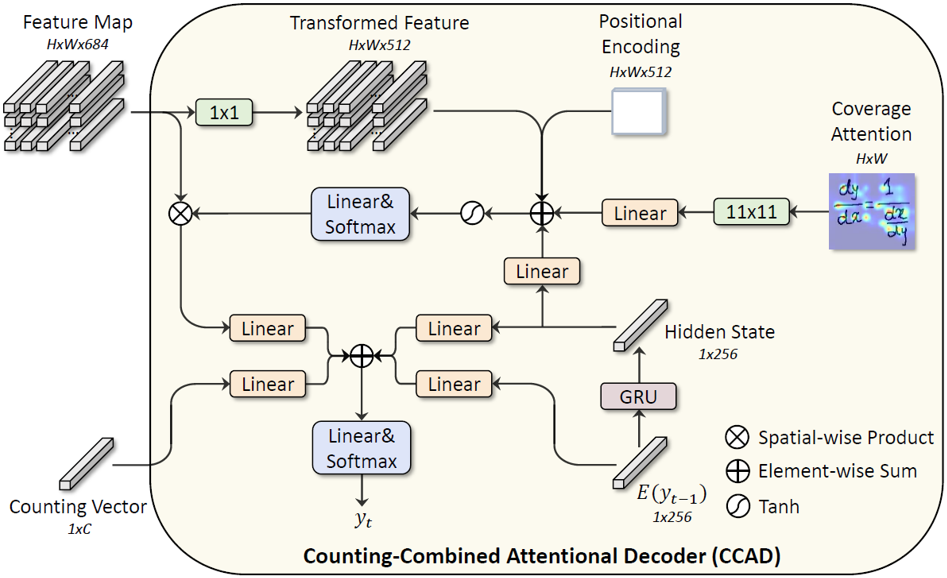
图5 结合计数的注意力解码器CCAD