在NLP领域多任务学习可以使得相似任务之间共享信息,获得更好的收益,但是要进行多任务学习的前提是要有一份多任务的标注数据,这里说的标注数据是说任务之间共享一份相同的输入数据,但是是不同的标注任务。上叙述的标注语料通常来说是比较昂贵,而主动学习可以很好的缓解这一困境,两则结合便成了今天要介绍的MT-AL即多任务学习:Multi-task;主动学习:Active learning;本篇并不是探究MT-AL的第一篇,而本篇是第一次尝试端到端的MT-AL,感兴趣的来看看吧~
论文链接:https://arxiv.org/pdf/2208.05379.pdf
Confidence Estimation
主动学习的一个最基本思路就是每次从未标注的样本中选出最困难的样本(所谓最困难就是模型最难识别的样本),然后人工标注,最后把这部分样本加入到训练样本中一起训练。
如此以往,多次迭代,直到收敛。可以看到其中最关键的步骤就是选困难样本,再说的直白点就是怎么量化困难这一含义,为此这里介绍了几种,具体的分为单任务和多任务两个方面来介绍:
先来看单任务:Random (ST-R):这里就是随机选,可以当作一个baselineEntropy-based Confidence (ST-EC) :使用熵来量化
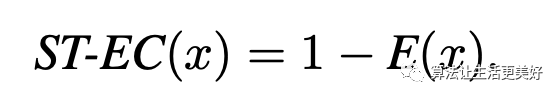
E(x)就是熵,相信大家也比较熟悉,其越大代表着结果越不确定,所以ST-EC(x)越小越代表着困难样本。Dropout Agreement (ST-DA) :这里借鉴了Ensemble方式即通过多个模型来综合决定最后的分数说完了单任务的,再来看看多任务的,其实和单任务一样,对应的为MT-EC 和MT-DA,只不过这里是多个任务,那就是说一个样本对应多个量化指标,所以最后得聚合一下得到一个总的量化值,具体的聚合方式也非常的常见就是平均值、最大值、最小值即MT-AVGDA、MT-MAX、MT- MIN。
多任务的量化指标除了上面容易想到的简单指标,作者这里还提出了另外三个MT-PAR、MT-RRF和MT-IND。首先说第一个即把每一个样本的不确定量化值看成一个向量,假设有n个任务,那么该向量值就是一个n维的向量,向量中的每一个值代表当前任务的一个量化值,如果一个样本对应向量中存在一个元素小于其他所有样本的向量对应位置的元素或者一个样本所有元素都小于其他样本向量对应位置元素的时候,这个样本就叫做边界点,而这样样本就是被选择的困难样本,当通过这种方式选出了的样本数量小于规定的样本数时,那就先把这部分样本选出来,然后在剩下的样本中重复上述逻辑,直到达到规定的数量,当超出时,那就选第一个维度先进行排序,然后等间隔选择出规定的数量。其次来看MT-RRF,对于每一个样本首先计算得到其t个任务对应的ST-EC值,然后假设对于某一个任务,我们对所有样本进行排序,具体的是ST-EC值从小到大排序,然后每一个样本就可以得到其t个任务对应的ST-EC排序值即r,最后样本x的MT-RRF值就是倒排,公式如下:
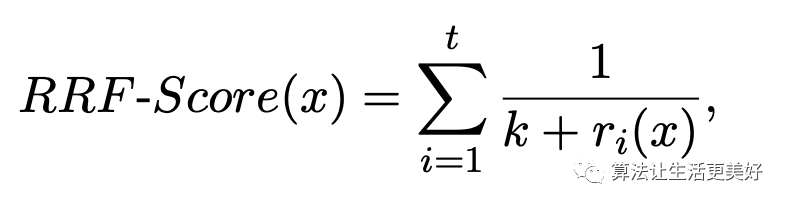
然后在选择的时候,优先选择MT-RRF值大的值,因为MT-RRF值越大意味着其各个任务的排序就越小,意味着其各个认为的ST-EC值排序地位就越靠前,就意味着其各个任务的ST-EC值越小,就意味着越是困难样本。
最后来看MT-IND就更简单粗暴了,假设要选n个样本,一个t个任务,那么就每个任务选出n/t个样本,具体的也是根据ST-EC值。看到这里,大家应该就更清楚了,其实本质上用的基本都是ST-EC,只不过对于多任务就是怎么想办法把多个任务的ST-EC值聚合成一个,为此作者想了MT-PAR、MT-RRF和MT-IND三个值。
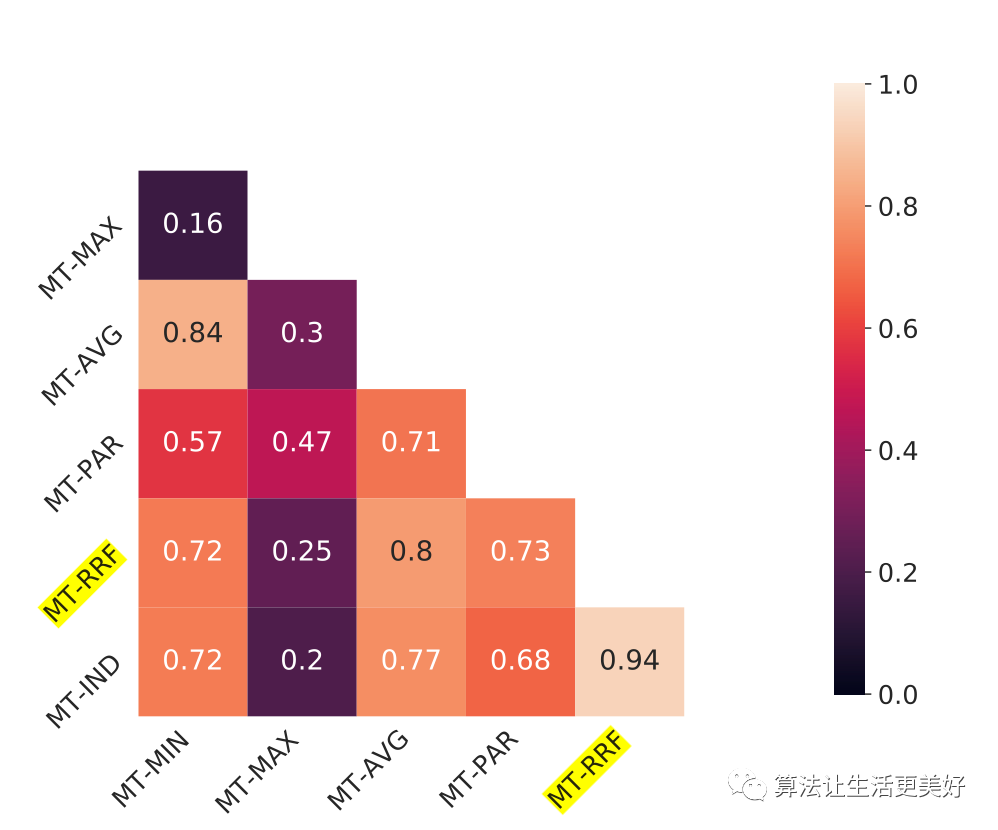
通过上面几种方式选出的困难样本,可以看到有很多交叉的Model
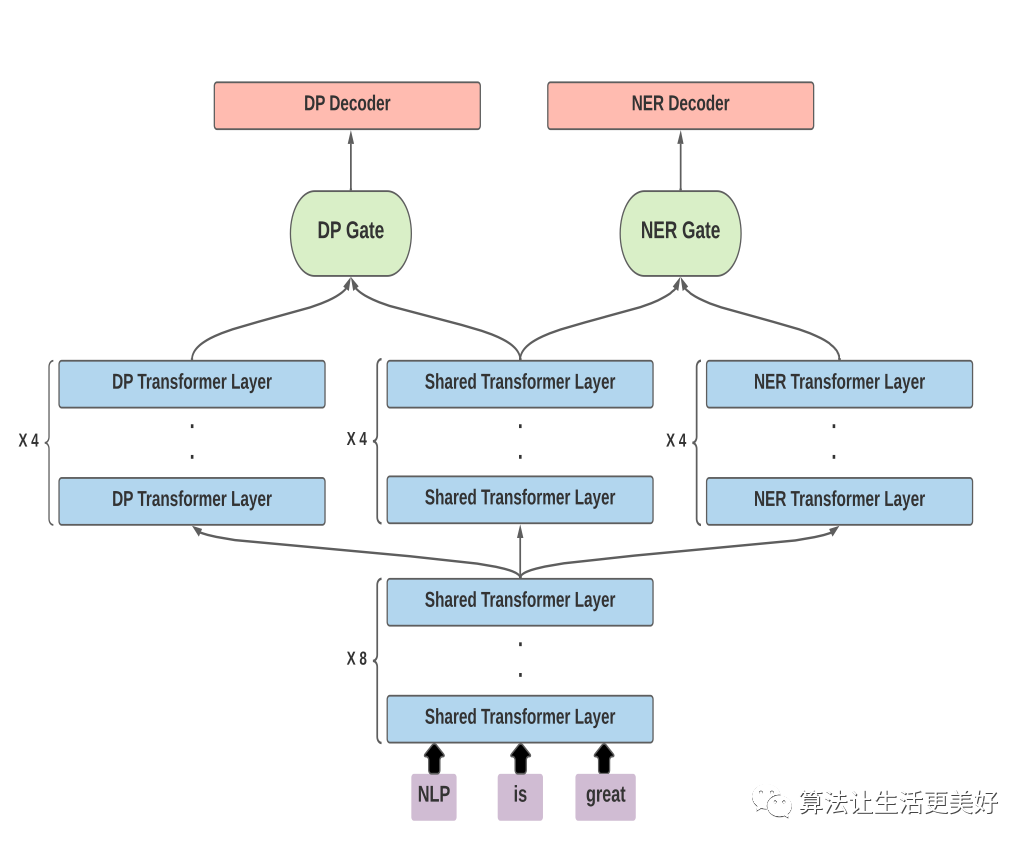
模型如下,这里有两个任务DP和NER任务,有一个底层共享的transformer和自己交叉的模型,模型图也比较清楚
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢