
论文链接:
https://arxiv.org/abs/2207.08877
代码链接:
https://github.com/tsun/KUDA
导读
在本文中,作者提出了参考先验知识来补偿目标域没有确定标记的问题,并针对两种关于目标域中类分布的特定类型的先验知识:描述单个类概率的上下界的一元界,以及描述两个类概率之间关系的二元关系,给出了通过先验知识细化伪标签的通用校正模块。这种模块它可以很容易地插入到基于自我训练的UDA方法中。作者将它与两种最先进的方法:SHOT and DINE相结合,提高了生成伪标签的质量,进一步提高了两种方法的性能。
贡献
深度神经网络在各种视觉任务中表现出显著的性能改进。然而,这样的性能高度依赖于大量的注释数据,而获得这些数据通常是昂贵的。无监督域自适应(UDA)通过将从标记的源域学习的预测模型转移到未标记的目标域来解决这个问题。尽管近年来取得了进展,但由于目标域中没有标签,UDA仍然是一项具有挑战性的任务。
另一方面,在许多实际应用中,关于目标域的先验知识通常是现成的。特别是,关于类分布的一些信息通常是可用的,而不需要麻烦标记特定的目标样本。例如,植物学家可以利用历史信息估计保护区内野生物种的比例;经济学家可以根据当地的产业结构判断货车是否比其他车辆拥有更多;这样的先验知识可以提供与未标记的训练数据互补的有价值的线索,并且在源域和目标域之间存在大的分布偏移时尤其有益。事实上,先前的知识已被用来弥补标记数据的不足,但其系统集成到UDA解决方案中仍有待探索。
受上述观察的启发,作者研究了一种新的UDA设置,名为知识引导的无监督域自适应(KUDA),如图1所示。具体而言,除了目标训练样本之外,还可以访问目标类分布上的先验知识集合。
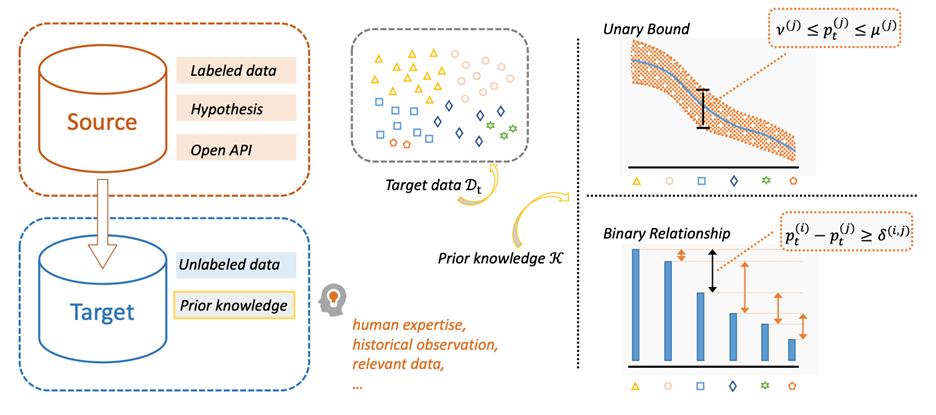
图1.1 KUDA及其先验知识
图1.1(左)知识引导的无监督域自适应(KUDA)。除了目标数据外,还可以获得有关目标类分布的一些先验知识。(右)本文考虑了两种类型的先验知识。
文中考虑了两种类型的先验知识:一元边界,描述单个类概率的上下界(例如,“平方”的t概率在0.1和0.3之间),二元关系,描述两类概率之间的关系(例如,“三角形”多于“平方”)。KUDA的任务是在这些先验知识的指导下,将从源域学习的预测模型调整到目标域。文中之所以选择一元和二元统计数据而不是类分布,是因为它们在实践中的通用性和可访问性。
为了将先验知识结合到领域自适应中,文中提出了一种新的校正模块来改进模型生成的伪标签。作者将使用先验知识的校正过程表述为零一规划(ZOP)问题,其中其最优解返回更新的伪标签。该模块可以很容易地集成到基于自训练的UDA方法中。为了验证其有效性,文中使用校正模块对两种最新的UDA方法,SHOT和DINE进行了改进。
实验验证是在四个常用的UDA基准点上进行的,其中两个在设计上具有较大的标签分布偏移。结果证实,校正模块提高了伪标签的质量,因此有利于自训练阶段。因此,与普通版本相比,在先验知识指导下的两种方法(分别命名为kSHOT和kDINE)的性能显著提高。实验表明,考虑目标类的先验知识非常重要,尤其是当领域差距较大时。
方法
一般情况下。假设有一个对于目标数据的模型预测类概率矩阵 \( P \in \mathbb{R}^{n_t \times C} \) 。其中第 i 个样本的伪标签可以通过 \( \hat y_i^t=\text{arg max} \) 获得,其中\( p_i \) 是 P 的第 i 行。该过程可以使用one-hot标签表示 \( l_i \)及其矩阵形式 L 以更紧凑的形式等效表示:
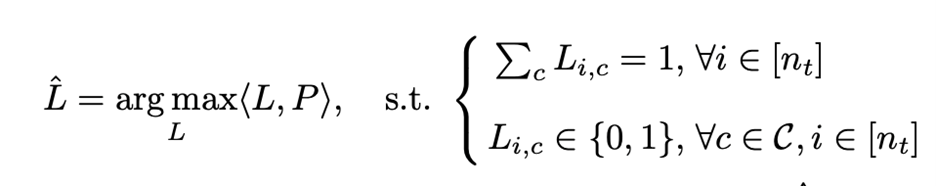
其中 ⟨⋅,⋅⟩ 是两个矩阵的内积,并且 \( [n_t ]=\{0,1,…,n_t-1\} \) 。该式的最优解为 \( \hat L_{i,\hat y _i^t}=1 \)以及\( \hat L_{i,c}=0 \forall c \neq \hat{y}_{i}^{t} \)。
在没有任何先验知识的情况下,为每个目标样本独立地分配最优 \( l_i \) 。经验概率 \( \hat{p}_{t}^{(c)}=\sum_{i} L_{i, c} / n_{t} \)应接近 \( p_t^{(c)} \) 。然而,由于模型预测 t 有噪声,实践中经常不能达到效果。文中使用 \( p_t \) 的先验知识 K 来校正伪标签。
对于之前叙述的不等式,插入\( \hat p_t \) 并将约束添加到等式1中的优化问题中。可以得到硬约束形式的优化问题公式:
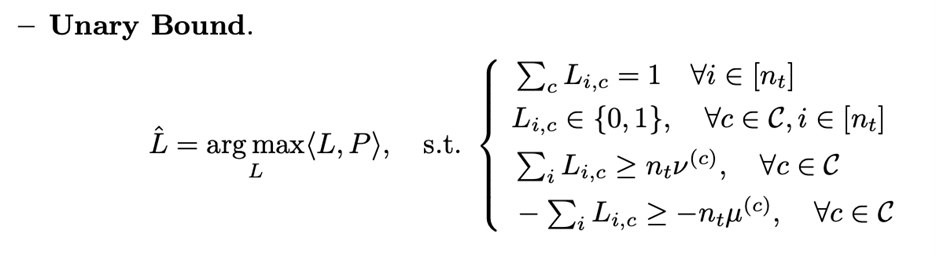
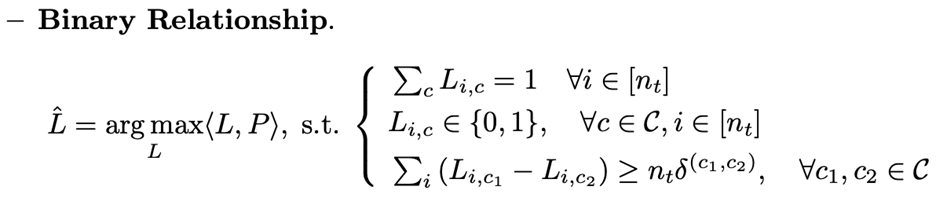
3.1 硬约束形式
上面的两式是0-1编程问题,可以用标准解算器求解。然而,使用硬约束形式是不可取的。当这些约束不一致时,优化问题变得不可行。为了克服硬约束形式的缺点,文中通过引入松弛变量将先验知识转化为软约束:
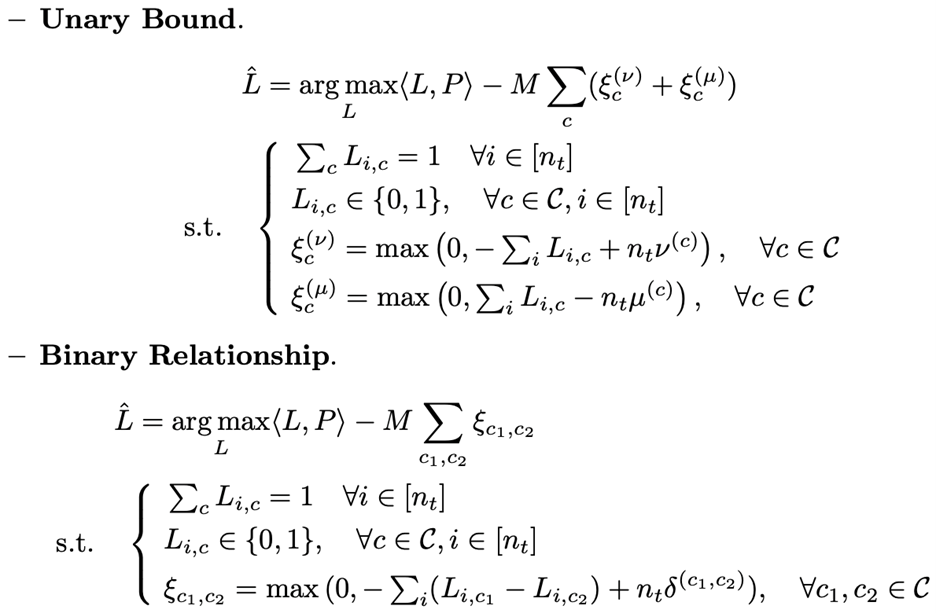
3.2 软约束形式
在软约束的等式中中, M 是预定义的非负常数。当 M 足够大时,只要来自先验知识的硬约束是可满足的,它们的解将分别与硬约束时的解相同。当 M=0 时,软约束将退化为针对原问题的基础问题。
3.3 平滑正则化
以前的优化问题利用关于类分布的先验知识来改进伪标签。然而,这仅依赖于模型预测概率矩阵 PP ,而不考虑特征空间中的数据分布。在分类任务中,预期标签预测是局部平滑的。因此,作者添加了一个平滑正则化,使相邻样本的伪标签保持一致。
文中选择模型预测不确定的目标样本的子集\( \mathcal{S}_{t} \subseteq \mathcal{D}_{t} \)。让每个 \( x_i^t \in \mathcal{S}_t \) 在 \( \mathcal{D}_{t} \backslash \mathcal{S}_{t} \) 中的最近邻为 \( x_{ki}^t \)。平滑正则化是等约束的集合, \( \mathcal{R}=\left\{\left({l}_{i}={l}_{k i}\right) \mid {x}_{i}^{t} \in\right. \left.\mathcal{S}_{t}\right\} \) 。将这些等式转换为软约束是非常重要的,因为它将在目标中引入二阶项。这些等式是硬约束时,无法直接将它们添加到上面两个等式中。
3.4 kSHOT和kDINE
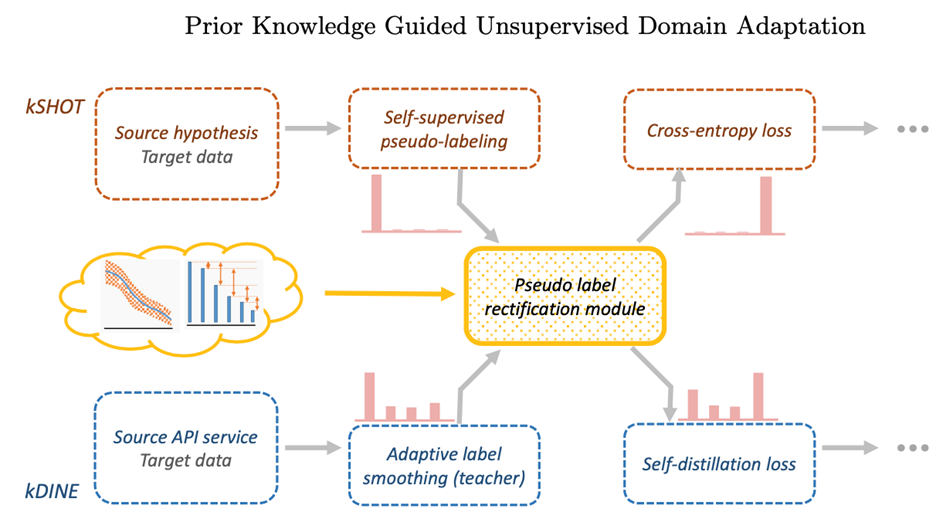
图2.4.2校正模块集成到SHOT和DINE中的过程示意图。可以以类似的方式容易地扩展到其他基于自训练的UDA方法。
文中提出的校正模块可以很容易地插入到基于自训练的UDA方法中。文中选择了两种最新的UDA算法,SHOT和DINE,来验证其有效性。利用先验知识指导的kSHOT和kDINE如图2.4.2所示。
实验
作者在 office-home,VisDA-2017,DomainNet ,office以及PDA五个数据集上分别对知识引导下SHOT以及DINE两种方法的准确率提升进行了实验和计算。实验结果如下:
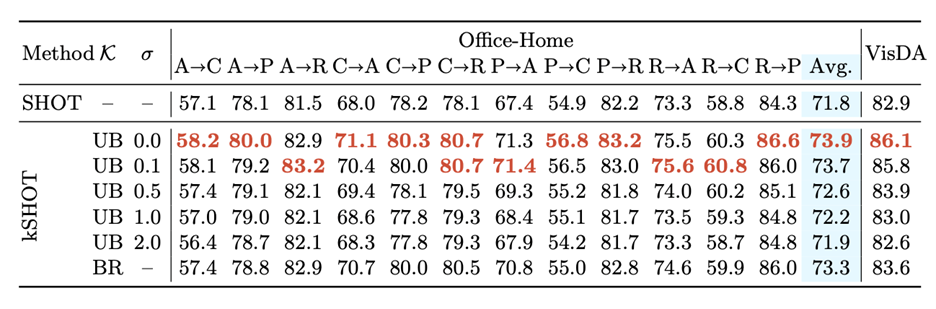
图3.1 SHOT,kSHOT方法在office-home以及VisDA上的测试结果
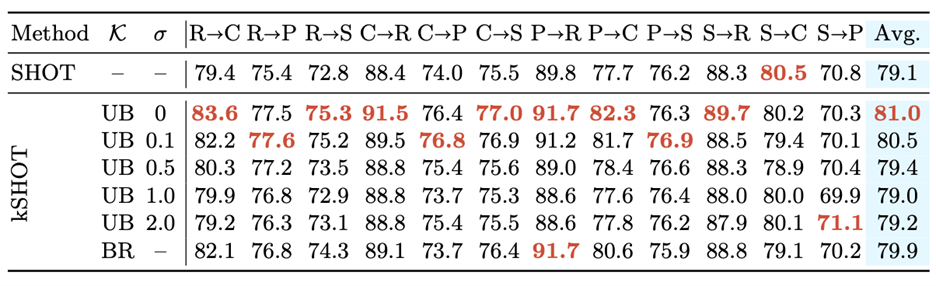
图3.2 SHOT,kSHOT方法在DomainNet 上的测试结果
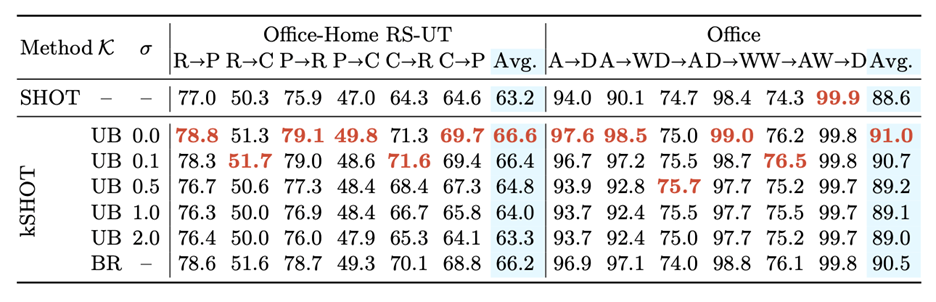
图3.3 SHOT,kSHOT 方法在office-home RS-UT以及 Office 上的测试结果
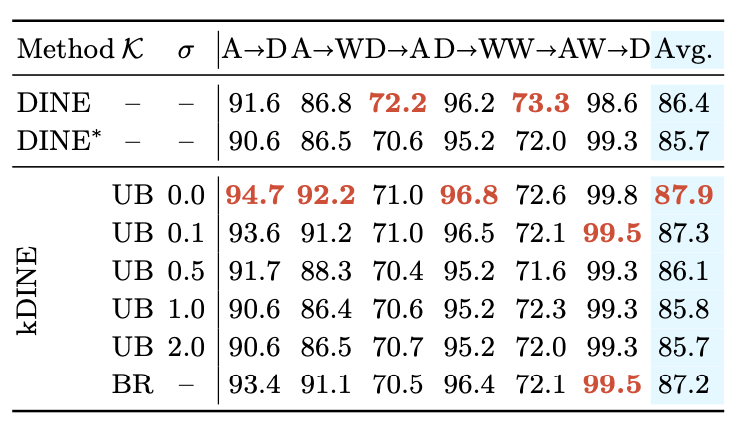
图3.4 DINE,DINE*,kDINE方法在office上的测试结果
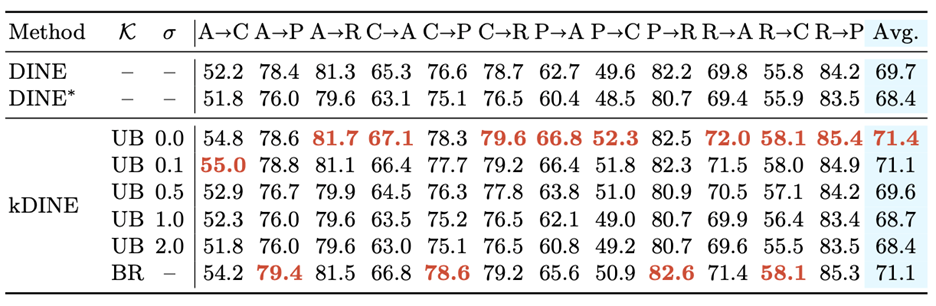
图3.5 DINE,DINE*,kDINE方法在office-Home上的测试结果
经过测试,当先验知识充足时,kSHOT在Office Home RS-UT上的准确率相对于SHOT提高了+3.4%,在DomainNet上提高了+1.9%。随着先验信息量的减少kSHOT的准确率逐渐接近SHOT。对PDA上的实验则证明·当数据具有长尾性时,使用先验知识对准确率的提高更大。
经过分析,先验知识可以从以下几点指导UDA:
- 可以帮助归类模棱两可的样本
- 可以改善样本的伪标签分布使其更接近真实情况
- 即使在先验知识中含有较多噪声时或仅有部分先验知识,仍能起到优化UDA的作用。
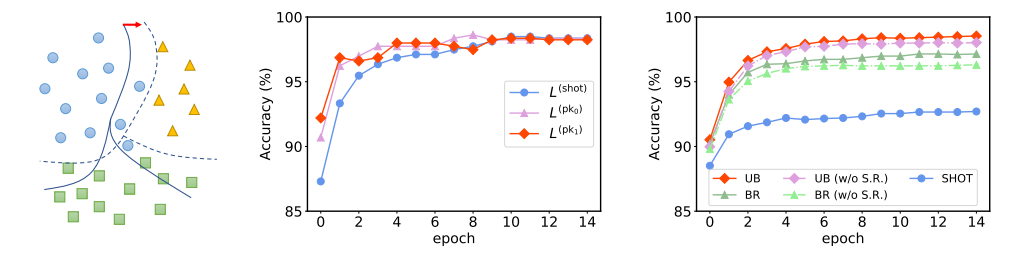
图3.6 (左)先验知识纠正模糊样本的伪标签;(中心)kSHOT在数据集Office A→W上训练时,使用事先知识纠正前后伪标签的准确度(右)Office A→W上的收敛曲线比较图(S.R.是平滑正则化的缩写)。
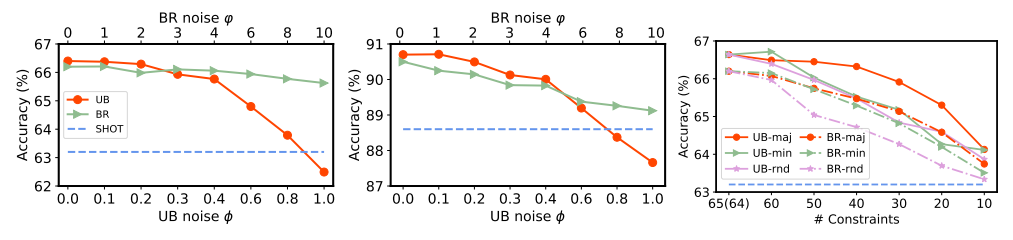
图3.7 在(左)Office US-RT (中)Office 数据集上应用先验知识有噪声的kSHOT时的准确率曲线:在 Office US-RT 数据集上应用不完全先验知识的kSHOT 时的准确率曲线
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢