
经典机器学习(ML)为解决物理和化学中具有挑战性的量子多体问题提供了一种潜在的强大方法。然而,ML 相对于传统方法的优势尚未得到牢固确立。
在一项新的工作中,加州理工学院的研究人员证明了经典的 ML 算法在向物质相同量子相中的其他哈密顿量学习后,可以有效地预测带隙哈密顿量的基态特性。相比之下,在一个被广泛接受的猜想下,不从数据中学习的经典算法无法实现同样的保证。
该团队还证明了经典的 ML 算法可以有效地对各种量子相进行分类。大量的数值实验证实了他们在各种场景中的理论结果,包括里德堡原子系统、二维随机海森堡模型、对称保护拓扑相和拓扑有序相。
该研究以「Provably efficient machine learning for quantum many-body problems」为题,于 2022 年 9 月 23 日发布在《Science》。

解决量子多体问题,例如寻找量子系统的基态,对物理学、材料科学和化学具有深远的影响。经典计算机促进了科学和技术的许多深刻进步,但它们往往难以解决这些问题。可扩展、容错的量子计算机将能够解决广泛的量子问题,但在未来几年内不太可能出现。同时,如何才能最好地利用强大的经典计算机来促进对复杂量子系统的理解?
最近,经典机器学习 (ML) 技术已被用于研究量子多体物理中的问题。到目前为止,这些方法大多是启发式的,反映了 ML 中严格理论的普遍缺乏。尽管它们已被证明在一些中等规模的实验中是有效的,但这些方法通常没有令人信服的理论论据来确保良好的性能。
一个中心问题是,经典 ML 算法是否可以在具有挑战性的量子多体问题中证明优于非 ML 算法。加州理工学院的研究人员通过设计和分析用于预测量子系统基态特性的经典 ML 算法来提供具体的答案。该团队证明,这些 ML 算法可以在从测量同一量子相中的其他基态获得的数据中学习后,有效且准确地预测间隙局部哈密顿量的基态特性。
此外,在一个被广泛接受的复杂性理论猜想下,他们证明没有不从数据中学习的有效经典算法可以实现相同的预测保证。通过从实验数据中进行概括,ML 算法可以解决在没有访问实验数据的情况下,无法有效解决的量子多体问题。
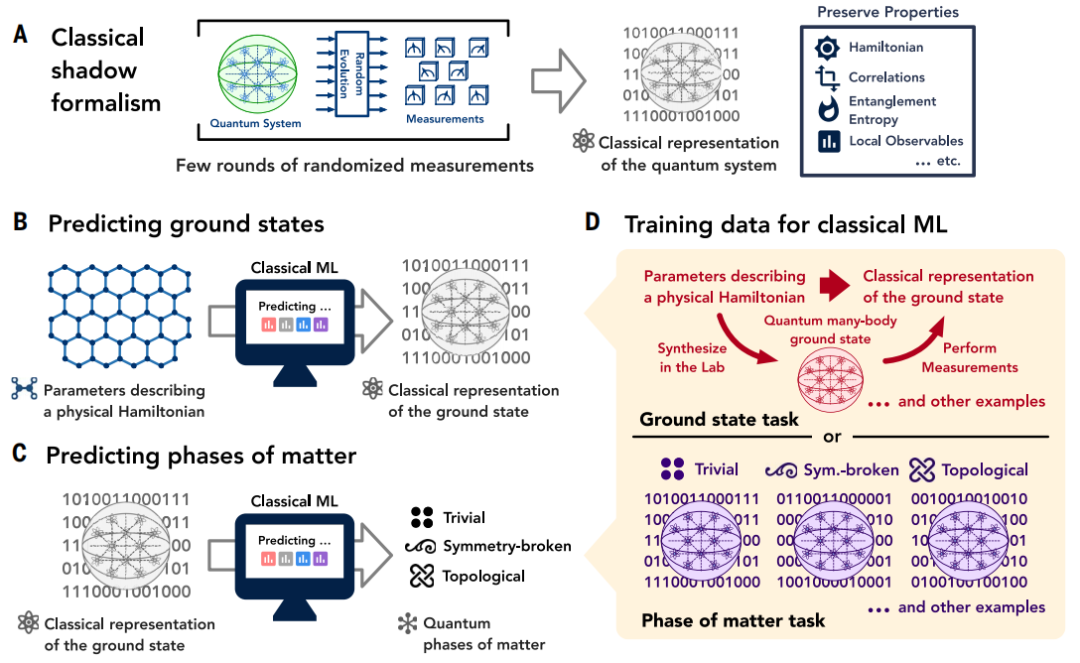
图示:中心概念。(来源:论文)
研究人员考虑了一系列有间隙的局部量子哈密顿量,其中哈密顿量 H(x) 平滑地依赖于 m 个参数(用 x 表示)。ML 算法从一组由 x 的采样值组成的训练数据中学习,每个采样值都伴随着 H(x) 的基态的经典表示。这些训练数据可以从经典模拟或量子实验中获得。
在预测阶段,ML 算法为哈密顿量预测与训练数据中不同的基态的经典表示;然后可以使用预测的经典表示来估计基态属性。具体来说,这里经典 ML 算法预测基态中局部可观察的乘积的期望值,在 x 的值上平均时有一个小的误差。算法的运行时间和训练数据量都需要以 m 为单位进行多项式缩放,并与量子系统的大小呈线性关系。
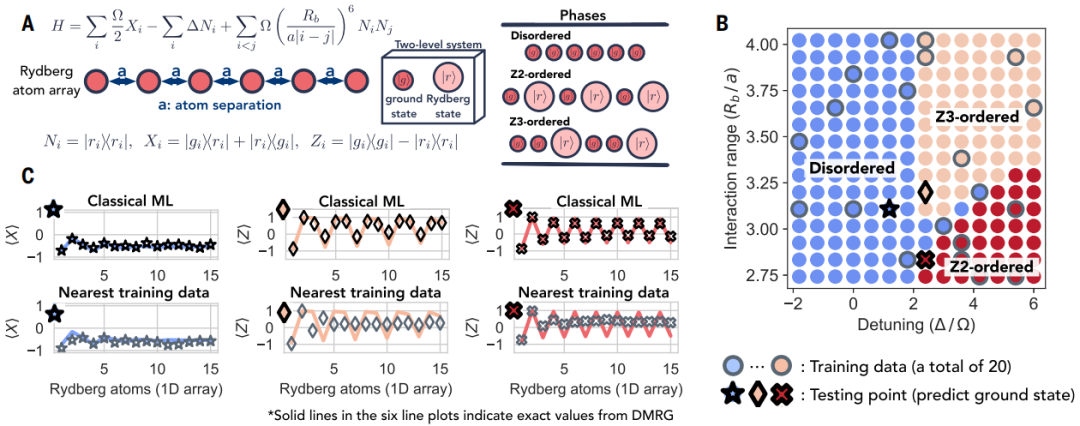
图示:预测具有 51 个原子的一维里德堡原子系统中基态特性的数值实验。(来源:论文)
研究人员对这一结果的证明建立在量子信息理论、计算学习理论和凝聚态理论的最新发展之上。此外,在普遍接受的猜想下,非确定性多项式时间(NP)完全问题不能在随机多项式时间内解决,该团队证明,任何不从数据中学习的多项式时间经典算法都无法与 ML 算法实现的预测性能相匹敌。
在使用类似证明技术的相关贡献中,该团队展示了经典 ML 算法可以有效地学习如何对物质的量子相进行分类。在这种情况下,训练数据由量子状态的经典表示组成,其中每个状态都带有一个标签,表明它属于 A 相还是 B 相。然后,ML 算法预测训练期间未遇到的量子态的相位标签。经典的 ML 算法不仅对相位进行准确分类,而且构造了显式的分类函数。数值实验验证了他们提出的机器学习算法在各种场景中都能很好地工作,包括里德堡原子系统、二维随机海森堡模型、对称保护拓扑相和拓扑有序相。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢