
图神经网络对非欧式空间数据建立了深度学习框架,相比传统网络表示学习模型,它对图结构能够实施更加深层的信息聚合操作。近年来,图神经网络完成了向复杂图结构的迁移,诞生了一系列基于复杂图的图神经网络模型。然而,现有综述文章缺乏对复杂图神经网络全面、系统的归纳和总结工作.将复杂图分为异质图、动态图和超图3种类型。将异质图神经网络按照信息聚合方式划分为关系类型感知和元路径感知两大类,在此基础上,分别介绍普通异质图和知识图谱.将动态图神经网络按照处理时序信息的方式划分成基于循环神经网络、基于自编码器以及时空图神经网络三大类。将超图神经网络按照是否将超图展开成成对图划分为展开型和非展开型两大类,进一步按照展开方式将展开型划分成星形展开、团式展开和线形展开3种类型。详细阐述了每种算法的核心思想,比较了不同算法间的优缺点,系统列举了各类复杂图神经网络的关键算法、(交叉)应用领域和常用数据集,并对未来可能的研究方向进行了展望。
http://www.jos.org.cn/jos/article/abstract/6626
1 背景与分类
图(Graph)作为一种数据结构, 能够精确描述事物间复杂的相互作用关系, 因而被广泛应用于诸多科学和 工程领域. 近年来, 由于图结构丰富的信息表达能力, 利用机器学习对图进行分析的研究受到越来越多的关 注. 图表示学习, 便是将图中丰富的结构和语义信息转化成低维稠密的节点表示向量, 以便于后续利用机器 学习方法进行诸如节点分类、链接预测和知识推断等图相关应用. 其中, 图神经网络(graph neural networks, GNNs)由于对图结构建立了深度学习框架, 相比于 DeepWalk[1]、Node2vec[2]等传统网络表示学习方法, 可以同 时利用图结构信息和节点特征信息, 并构造更加复杂深层的神经网络进行表示学习, 因而逐渐成为了近年来 的研究热点.
为了简化问题和便于建模, 早期的图神经网络大多基于简单图结构, 即静态、同质的成对图结构. Sperduti 等人[3]最早尝试将神经网络应用到有向无环图上. 他们提出了一个将输入的图结构转化成固定维度的节点向 量的编码器, 并将向量输入到一个前馈神经网络中进行分类. 在此基础上, Gori 等人[4]首次提出了图神经网络 的概念, 他们将递归神经网络(recursive neural network, RNN)扩展到了图结构, 进而提出了递归图神经网络. 由此衍生出一系列早期图神经网络研究[5,6]. 然而, 这些早期方法有着很高的计算复杂度, 难以应用到大型图 结构上, 因此并没有得到广泛应用.
近年来, 得益于卷积神经网络(convolutional neural network, CNN)在计算机视觉领域的成功, 许多方法开 始尝试对图结构定义卷积操作, 并将卷积神经网络迁移到图结构上. 这些方法统称为图卷积神经网络(graph convolutional networks, GCNs). 图卷积神经网络可以按照实施卷积的方式分为谱方法(spectral-based GCNs)和 空间方法(spatial-based GCNs)两种类型. 其中, 谱方法利用卷积定理从谱域定义图卷积. 例如, Xu 等人提出的 GWNN[7]引入小波变换替换傅里叶变换作为基底, 使得模型拥有更好的局部性; Defferrard 等人[8]和 Kipf 等 人[9]通过对卷积核参数化, 实现了局部性并降低了复杂度. 空间方法则致力于从节点所在的空间域出发, 通 过定义聚合操作和连接操作来聚合邻居信息并与中心节点信息合并从而形成新的中心节点表示. 例如, MPNN[10]将图卷积转化成节点间信息的传递, 并提出了空间方法的一个通用框架. 后续的 GraphSage[11]使用 采样选取固定数量的邻居节点, 并给出更加丰富的聚合函数类型.
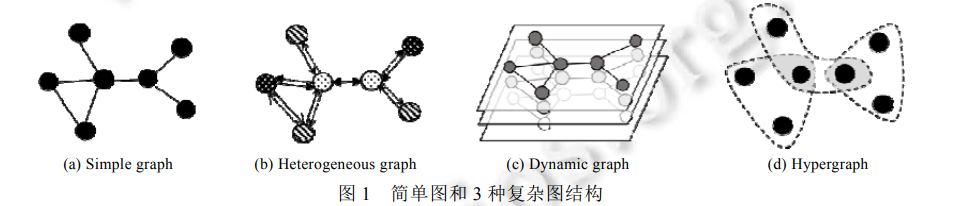
随着 GNNs 在简单图上的逐渐完善, 人们开始考虑更加复杂多样的图结构. 通过赋予图异质性、时序性 或高阶关联等特征, GNNs 衍生出了一大批基于复杂图结构的变种, 使其拥有更加灵活广泛的应用场景. 本文 按照复杂图的结构类型将这些方法分为异质图、动态图和超图三大类. 图 1 表示了简单图和 3 种复杂图结构
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢