摘要
数学模型正变得包含越来越多的细节,以更好地在缺少可用的训练或验证数据集时,预测现象或获得对动力系统更准确的洞察力。近日发表于 Science Advances 的论文通过方差分析和统计理论表明,这种做法会带来更多的不确定性和模糊的预测,因为它增加了模型的有效维数,即有影响的参数数量和高阶相互作用的权重。通过跟踪每个模型变得复杂过程中的有效维度和输出不确定性的演变,建模人员可以更好地思考增加的细节是否真正符合模型的目的,以及输入到模型中的数据的质量。
这篇题为“更高有效维度的模型会带来更大的不确定性”的论文让我们回归科学的一条核心原则:奥卡姆剃刀——如无必要,勿增实体。
关键词:模型复杂度,不确定性,有效维度

论文题目:
Models with higher effective dimensions tend to produce more uncertain estimates
论文链接:https://www.science.org/doi/10.1126/sciadv.abn9450
- 模型不是越复杂越好
许多数学模型变得越来越复杂,建模者认为对研究过程的全面描述最终将约束不确定性,并产生更精准的洞察力。在缺少训练及验证数据时,这类模型(例如预测二氧化碳排放量或新冠感染者数量的模型)倾向于基于特定领域的物理定律或原理,因此可能将它们的估计、预测投射到未知领域,由此带来不确定性。当缺乏验证数据来评价模型的偏倚(即模型估计与可用数据的距离有多远),建模者无法从现有的统计工具中受益。
新研究指出,建模者可以通过计算模型的“有效维度”(effective dimensions),即有影响的参数和主动高阶效应的数量,来衡量模型开发的所有阶段的模型复杂性和不确定性之间的关系。有效维度的概念有助于根据应用领域的语境和建模目的,更好地调整模型的复杂性。该研究的量化证据表明,在基于过程的模型中增加模型细节,往往会产生更多(而不是更少)的不确定性估计,因为这增加了模型的有效维数,通常会增加输出方差。由于数学建模中不确定性和敏感性分析的缺乏,这一事实可能还没有被注意到,这表明应该重新评估对不断详细的数学模型的追求,以获得更准确的估计和更清晰的洞见。
- 真实模型中的不确定性
二氧化碳的排放量预估模型,通常基于对不同地理区域分割后得出。这样的模型中,引入的因果假设越多,就会有更多的二阶及三阶影响,从而使模型的不确定性增加,这里使用变异系数 Coefficient of Variation(CV) 评价。图1a中不同来源下CO2排放量预测模型,有效维度(kt)越高,变异系数越大,三阶效应所占的比例越大。
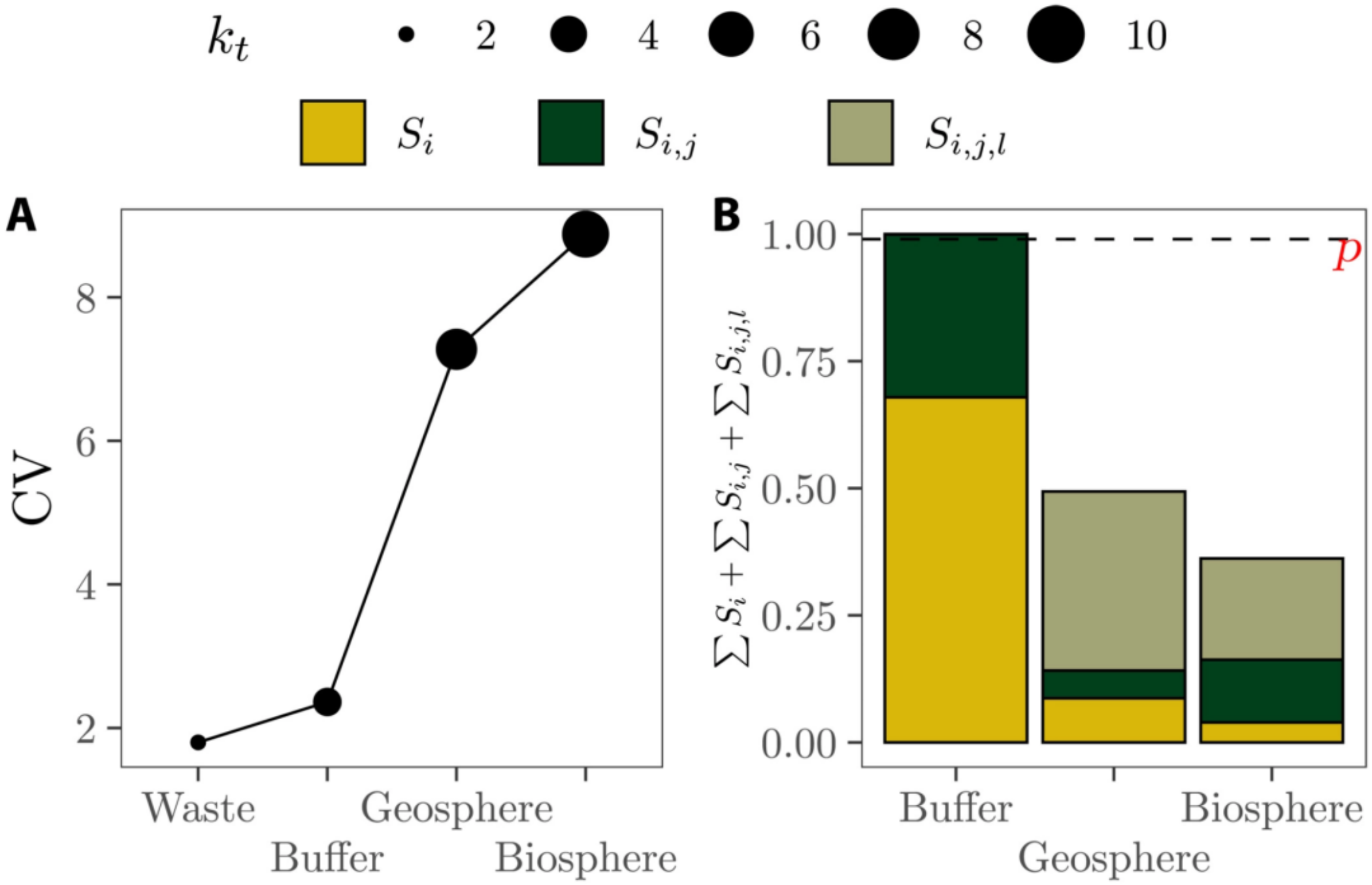
图1:PSACOIN 模型中复杂性和不确定性的关系
另一个例子是新冠感染者预测,考虑基本的SIR模型,以及加上了疫苗影响(S-V),以及不同疫苗策略后(S-E),可以看到越复杂的模型,不确定性越高(图2a, b),三阶效应所占的影响越大(图2c)。蒙特卡洛模拟也说明了这一情况(图3)。
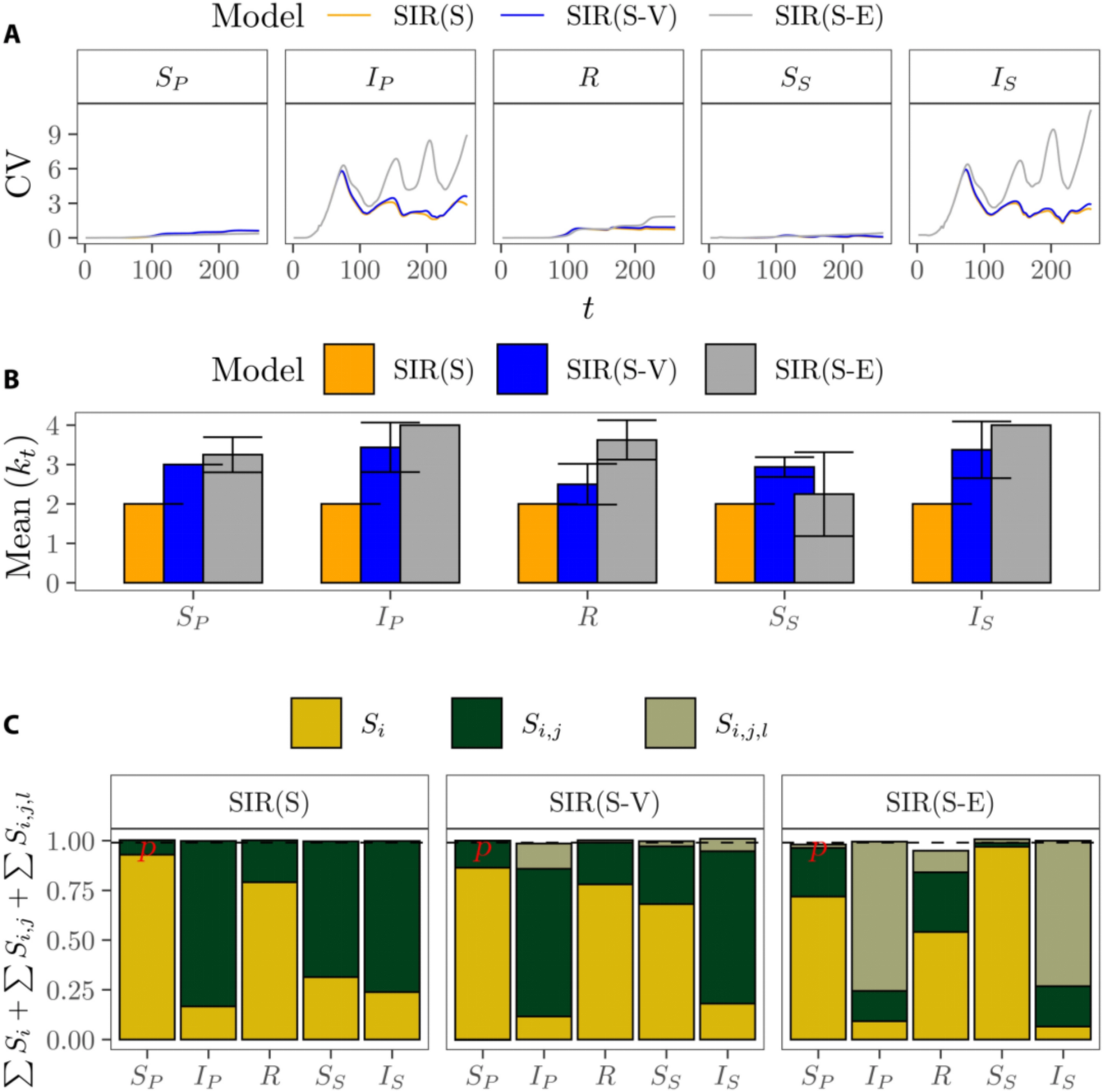
图2. (a) 易感者人数(Sp),感染者人数(Ip),康复者人数(R),免疫反应消失者人数(Ss)及二次感染后以较弱水平传播者人数(Is)在不同模型下随时间变化的变异系数;(b)预测上述值时,不同模型的有效维度;(c)预测上述值时,不同变量的二阶和三阶效应所占比。
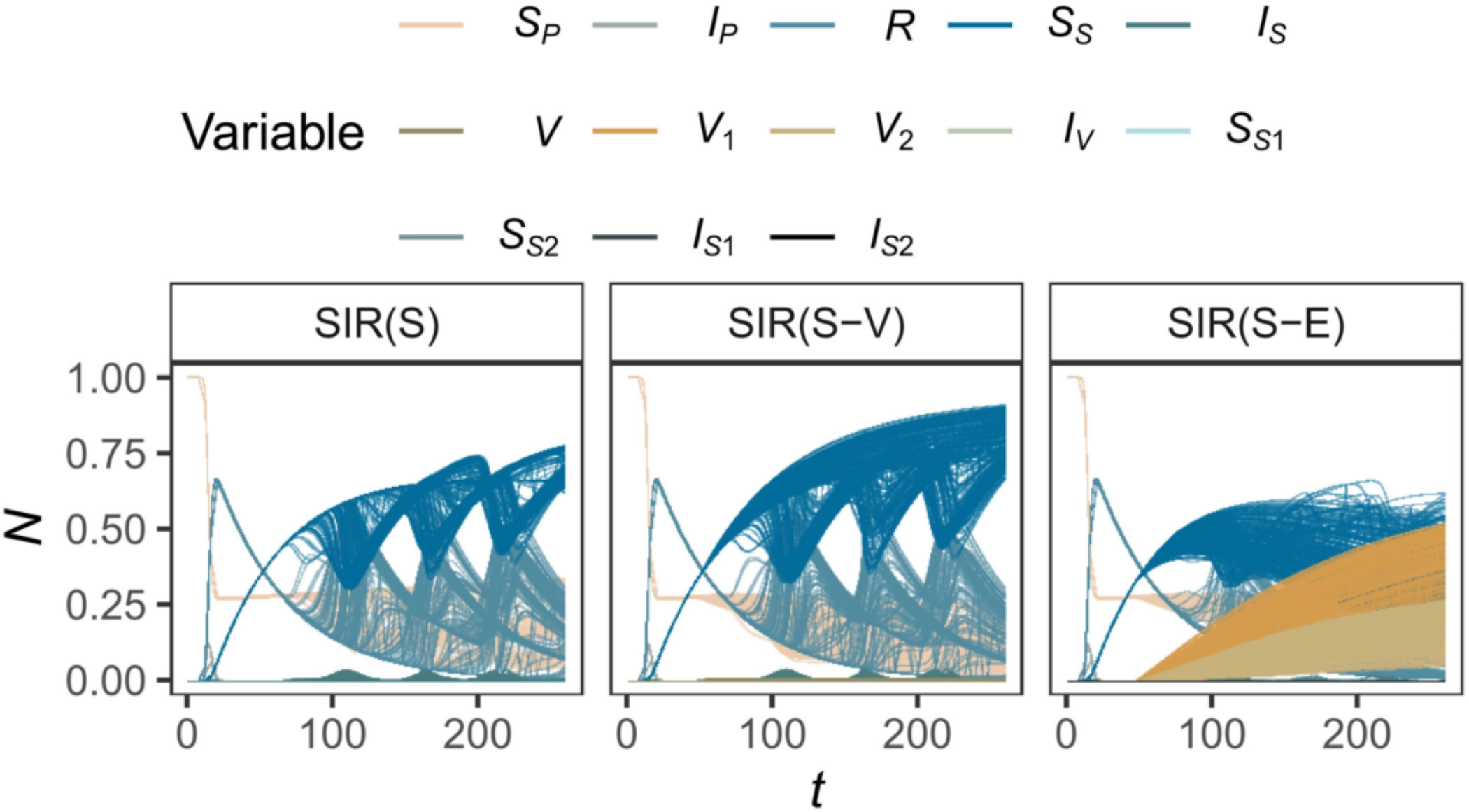
图3:经过蒙特卡洛模拟后,三种模型对不同变量的预测结果,可见越复杂的模型差异越明显
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢