
论文链接:https://arxiv.org/pdf/2112.07225.pdf
导读
长尾视觉识别任务对神经网络如何处理头部(常见)和尾部(罕见)类之间的不平衡预测提出了巨大挑战。模型倾向于将尾部类分类为头部类。虽然现有的研究侧重于数据重采样和损失函数工程,但在本文中,我们采用了不同的视角:分类间隔。我们研究了间隔(margin)和预测分数(logit)之间的关系,并凭经验观察到 「未校准的边距和预测分数呈正相关} 。我们提出了一种 「简单而有效的边距校准方法 (Margin Calibration,MARC) 来校准边距以获得更平衡的预测分数」,从而提升分类性能。我们通过对常见长尾基准(包括 CIFAR-LT、ImageNet-LT、Places-LT 和 iNaturalist-LT)的广泛实验来验证MARC。实验结果表明,我们的MARC方法在这些基准上取得了良好的结果。此外,「只需三行代码」 就能实现MARC。我们希望这种简单的方法能够激发人们重新思考长尾视觉识别中未校准的边距与预测分数之间的关系。
方法
在本文中,我们研究了 「间隔(Margin)」 和 「预测分数 (logits)」 之间的关系,这是主导长尾绩效的关键因素。
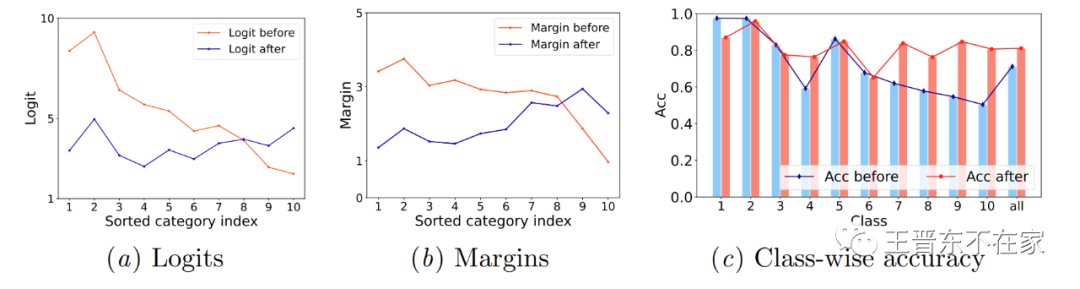
如下图所示,我们凭经验发现边距和预测分数与每个类的基数相关(一个类的基数即该类别拥有数据的数量)。具体来说,在校准之前,头类往往比尾类具有更大的边距和预测分数。因此,需要校准这种不平衡的边距以获得平衡的预测分数去避免未校准的边距对分类性能产生负面影响。
间隔校准方法MARC: Margin Calibration
我们提出一个简单的间隔校准方法 「MARC (margin calibration)」 来解决长尾问题。
具体而言,我们训练了一个简单的特定于类别的边距校准模型,其中原始边距 \( d_j \) 固定,\( w_j \) 和 \( \beta_j \) 是可学习参数:
\( \hat{d_{j}}=\omega_{j} \cdot d_{j}+\beta_{j} \)
\( d_{j} \) 的推理公式如下, 最终是由预测分数 ( \( logit=W_{j}z_{1}+b_{j} \) ) 除以线性分类器 (Linear Classifier Head) 的权重 (Weight) 的模 \( \left(\left\|\mathbf{W}_{j}\right\|\right) \)取得,其中 \( \mathbf{b}_{j} \) 为线性分类器的偏差 (bias) :
\( \begin{aligned} d_j & = \left\Vert proj_{ \mathbf{W}_j }(\mathbf{z}_1 - \mathbf{z}_0) \right\Vert \\ & = \left\Vert \frac{ \mathbf{W}_j \cdot (\mathbf{z}_1 - \mathbf{z}_0)}{\mathbf{W}_j \cdot \mathbf{W}_j} \mathbf{W}_j \right\Vert \\ & = \frac{\mathbf{W}_j \cdot \mathbf{z}_1 - \mathbf{W}_j \cdot \mathbf{z}_0 }{\Vert \mathbf{W}_j \Vert } \\ & =\frac{\mathbf{W}_j \mathbf{z}_1+\mathbf{b}_j}{\Vert \mathbf{W}_j \Vert} \quad (\text{since} \ \mathbf{W}_j \mathbf{z}_0 + \mathbf{b}_j = 0), \end{aligned} \)
因此,校准后的预测分数为
\( \begin{aligned} \Vert \mathbf{W}_j\Vert \hat{d_j} &=\Vert \mathbf{W}_j\Vert ( \omega_j \cdot d_j + \beta_j)\\ & = \omega_j \cdot \Vert \mathbf{W}_j\Vert d_j + \beta_j \cdot \Vert \mathbf{W}_j\Vert \\ & = \omega_j \cdot \eta_j + \beta_j \cdot \Vert \mathbf{W}_j\Vert, \\ \end{aligned} \)
其中 \( \eta_{j} \) 是固定的原始预测分数。
此外,我们还对不同类进行加权操作,最终通过训练 \( \omega_{j} \text { 和 } \beta_{j} \) 来获得更平衡的预测分数。
核心算法:仅需三行代码
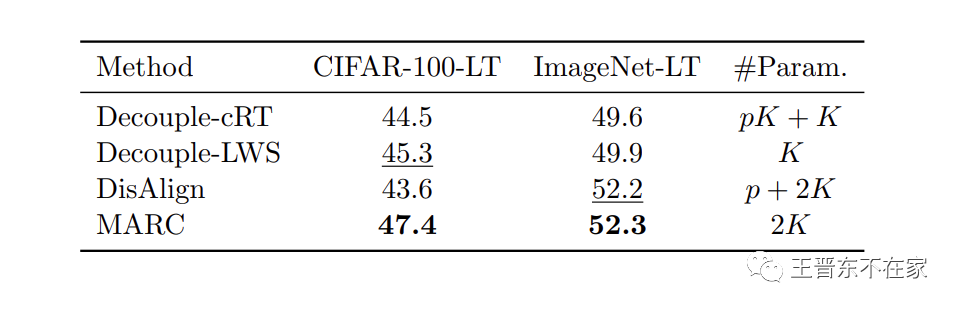
MARC可以被分类为决策边界(间隔)调整算法,其与之前的一些同类算法如Decouple (ICLR’20, 评论区提到的)和DisAlign等的区别如下:

MARC的核心算法如下图所示,核心部分如红框所示。「仅需三行代码」 即可实现MARC:

实验
分类结果
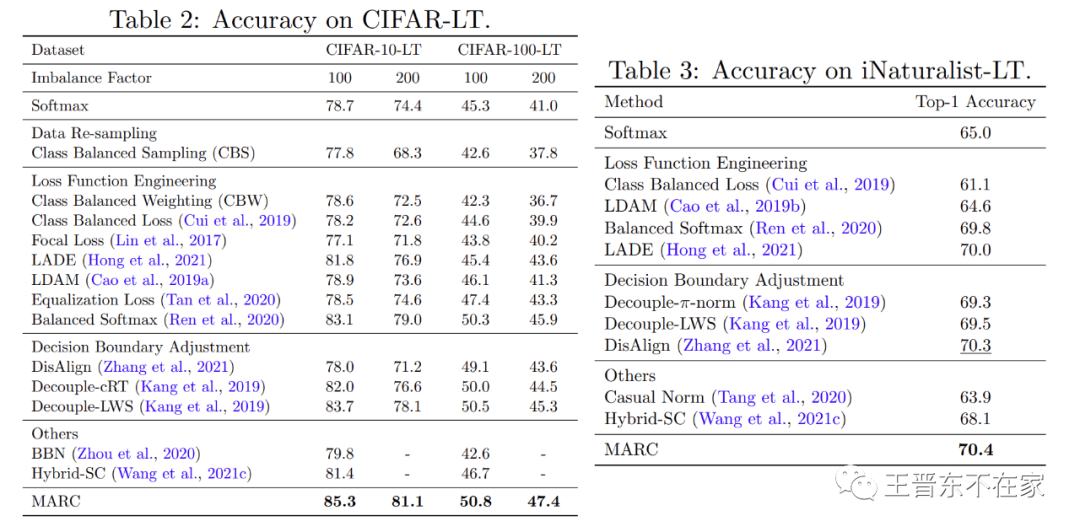
实验表格如下。我们在众多被广泛使用的长尾分类图像数据集中进行了对比。从实验结果可以看出MARC相比于其他方法取得了良好的性能,并且MARC十分容易实现。
复杂度
下图是MARC和另一个决策边界调整算法Dis-Align的对比试验,可以发现MARC取得了更平衡的边距和预测分数。
总结
本文研究了长尾视觉识别问题。具体来说,我们发现头类往往比尾类具有更大的边距和预测分数。受此发现的启发,我们提出了一个只有 2K(K是类别数)可学习参数的边距校准函数,以获得长尾视觉识别中的平衡预测分数。尽管我们的方法实现起来非常简单,但大量实验表明,与以前的方法相比,MARC在不改变模型表示的情况下取得了有利的结果。我们希望我们对预测分数和边距的研究能够为模型表示和边距校准的联合优化提供经验。未来,我们的目标是发展一个统一的理论来更好地支持我们的算法设计,并将该算法应用于更多的长尾应用。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢