【隐私计算笔谈】MPC系列专题（四）：GMW协议和BGW协议

GMW协议由Goldreich等人提出，基于混淆电路（Garbled Circuit），支持多方的半诚实的安全计算协议。和之前所述的姚氏混淆电路估值方案的不同之处在于，GMW混淆电路估值方案不需要使用混淆真值表，因此没用混淆真值表带来的查表和加解密操作，节省了非常大的计算量和通信量。

混淆电路在上次的科普已经介绍过了，在将安全多方计算的目标函数转换为布尔电路后，通过对电路进行混淆（加密）操作来得到混淆电路。

混淆电路通过对电路进行混淆（加密）操作来掩盖电路的输入和电路的结构，以此来实现对各个参与者的隐私信息的保密，再通过电路计算来实现安全多方计算的目标函数的计算。

GMW协议的目标函数由异或门和与门、非门组成。非门的输出值是输入值的反，输入为1则输出为0，反之输入为0则输出为1。与门的真值表如下图所示：

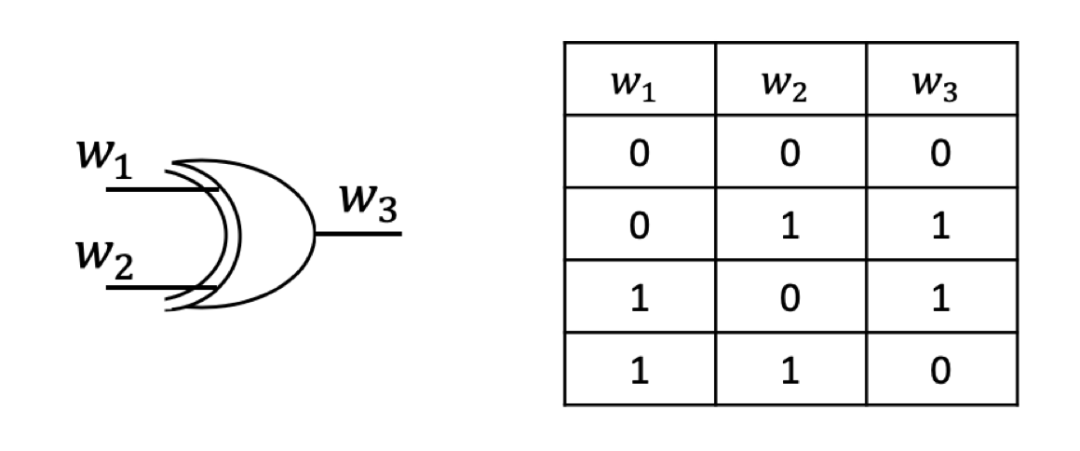
异或门及其真值表

异或门及其真值表如下图所示： 

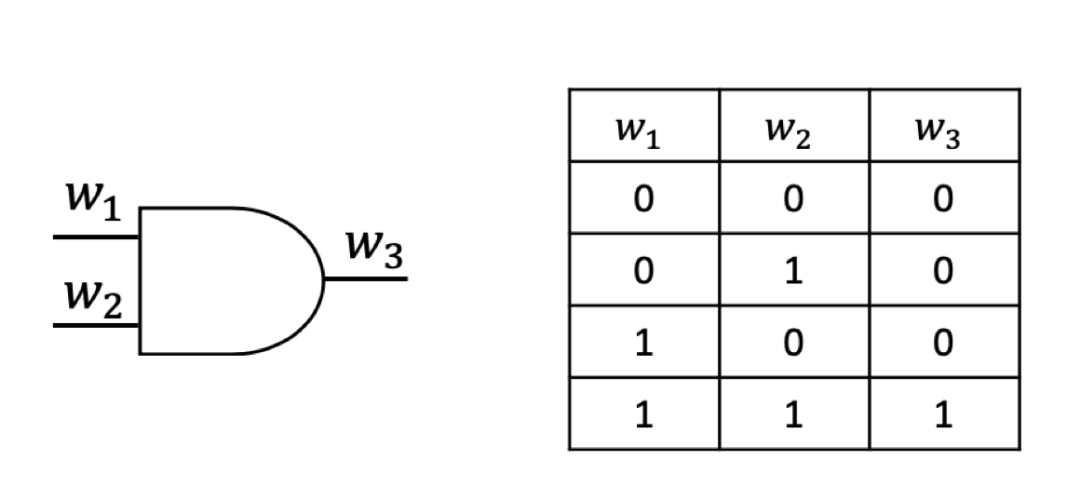
与门及其真值表

首先介绍GMW协议的两方情况。首先假设参与者为Alice 和Bob，Alice和Bob的输入均为长为n的比特串，其中 Alice输入为比特串𝑎，Bob的输入为比特串b。

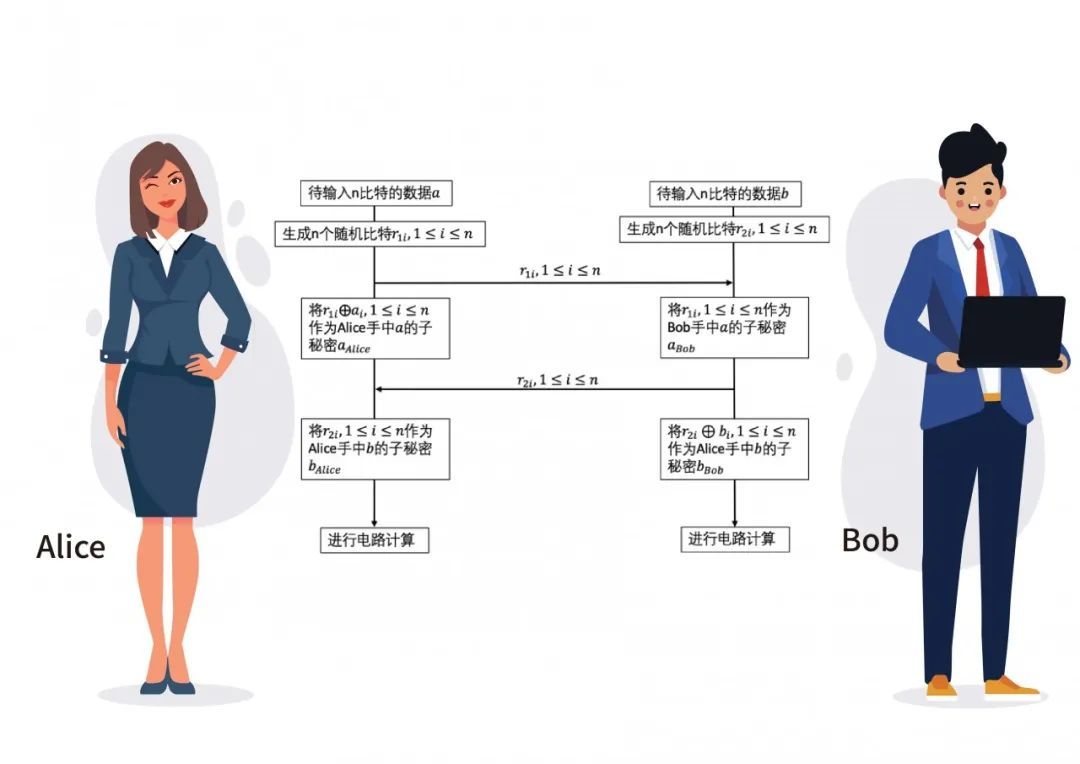
对于比特串𝑎中的每个比特𝑎_𝑖，Alice都产生一个随机的比特𝑟_1𝑖∈ {0,1},1≤𝑖≤𝑛，并将这n个随机产生的比特𝑟_1𝑖,1≤𝑖≤𝑛发送给Bob。

对于比特串𝑏中的每个比特𝑏_𝑖，Bob也都产生一个随机的比特𝑟_2𝑖∈ {0,1},1≤𝑖≤𝑛，并将这n个随机产生的比特发送给Alice。Alice和Bob分别将𝑎_𝑖⨁𝑟_1𝑖和𝑏_𝑖⨁𝑟_2𝑖、𝑟_1𝑖、𝑟_2𝑖作为协议输入𝑎和b的子秘密。

即Alice掌握了𝑎和b的子秘密𝑎_Alice和𝑏_Alice，𝑎_Alice=𝑎⨁𝑟_1𝑖，𝑏_Alice=𝑟_2𝑖，Bob掌握了𝑎和b的子秘密a_Bob和𝑏_Bob，a_Bob=𝑟_1𝑖，𝑏_Bob= 𝑏⨁𝑟_2𝑖。

若Alice公开其所掌握的𝑎⨁𝑟_1𝑖和𝑟_2𝑖，Bob公开其所掌握的𝑟_1𝑖和𝑏⨁𝑟_2𝑖，那么Alice和Bob可以共同计算出𝑎=𝑎⨁𝑟_1𝑖⨁𝑟_1𝑖，𝑏=𝑏⨁𝑟_2𝑖⨁𝑟_2𝑖。

接着Alice和Bob对布尔电路中的每个门求值，直至完成整个电路的计算。对于非门，由于非门是单输入的，Alice和Bob间无须进行交互，因此直接对输入求反即可。

对于异或门，假设异或门的输入分别为𝑎和b，Alice掌握了𝑎和b的子秘密𝑎_Alice和𝑏_Alice，Bob掌握了𝑎和b的子秘密a_Bob和𝑏_Bob，因为：

因此Alice和Bob可以在本地对其所掌握的子秘密进行计算，

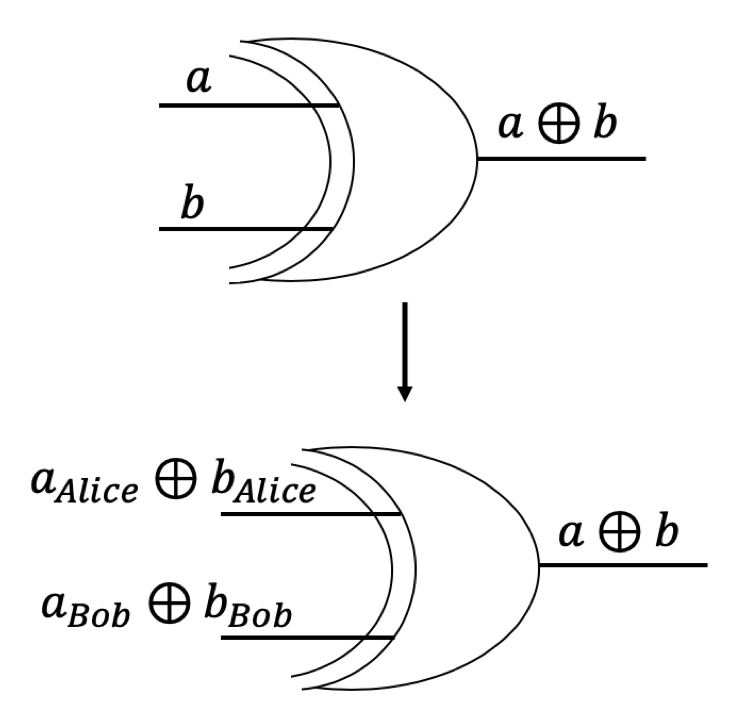
对于与门，因为𝑎⋀𝑏=(𝑎_Alice⨁a_Bob)⋀(𝑏_Alice⨁𝑏_Bob)，因此Alice和Bob无法只在本地完成与门的计算。

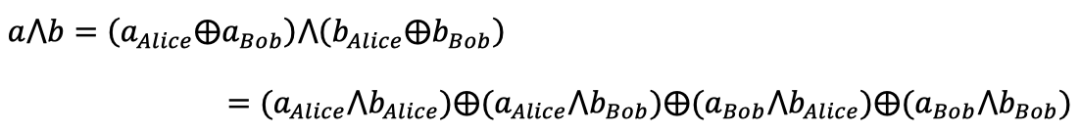
因为Alice手中有𝑎_Alice、𝑏_Alice，因此Alice可以本地计算𝑎_Alice⋀𝑏_Alice。Bob 手中有a_Bob、𝑏_Bob，因此Bob可以本地计算a_Bob⋀𝑏_Bob。剩下的𝑎_Alice⋀𝑏_Bob和a_Bob⋀𝑏_Alice二者必须协同完成。

(𝑎_Alice⋀𝑏_Bob)⨁(a_Bob⋀𝑏_Alice)的计算可通过四选一不经意传输协议完成。对于Alice来说，Bob掌握的a_Bob和𝑏_Bob都是单比特值，只有四种情况：

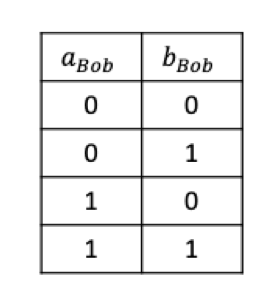
Alice手中又有𝑎_Alice和𝑏_Alice，因此Alice可以直接计算出四种情况下的𝑎⋀𝑏的值，假设分别为𝑐₀₀,𝑐₀₁,𝑐₀₁,𝑐_11，注意这里𝑎⋀𝑏的值为(𝑎_Alice⨁a_Bob)⋀(𝑏_Alice⨁𝑏_Bob)的值， 对于Alice和Bob来说式子里都只有两个未知数，而这两个未知数一共只有4种可能。

Alice的未知数为a_Bob和𝑏_Bob，Alice可以假设(a_Bob,𝑏_Bob)分别为(0,0)、(0,1)、(1,0)、(1,1)，那么根据假设的四种情况，𝑎_Alice,𝑏_Alicea_Bob,𝑏_Bob就都确定了，可以据此计算出四个确定的𝑐₀₀,𝑐₀₁,𝑐₀₁,𝑐₁₁值。因此Alice可以得到下表：

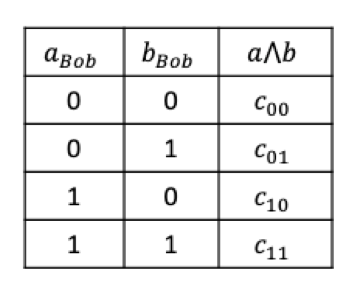
Alice 再产生一个随机比特𝑟，并将计算出的𝑐₀₀,𝑐₀₁,𝑐₀₁,𝑐₁₁异或上随机比特𝑟，将𝑐₀₀⨁𝑟, 𝑐₀₁⨁𝑟, 𝑐₀₁⨁𝑟, 𝑐₁₁⨁𝑟为四选一不经意传输协议的输入，Bob将其所掌握的a_Bob𝑏_Bob作为四选一不经意传输协议的输入，双方执行该OT协议，Bob得到对应的𝑐_aBob𝑏Bob⨁𝑟。

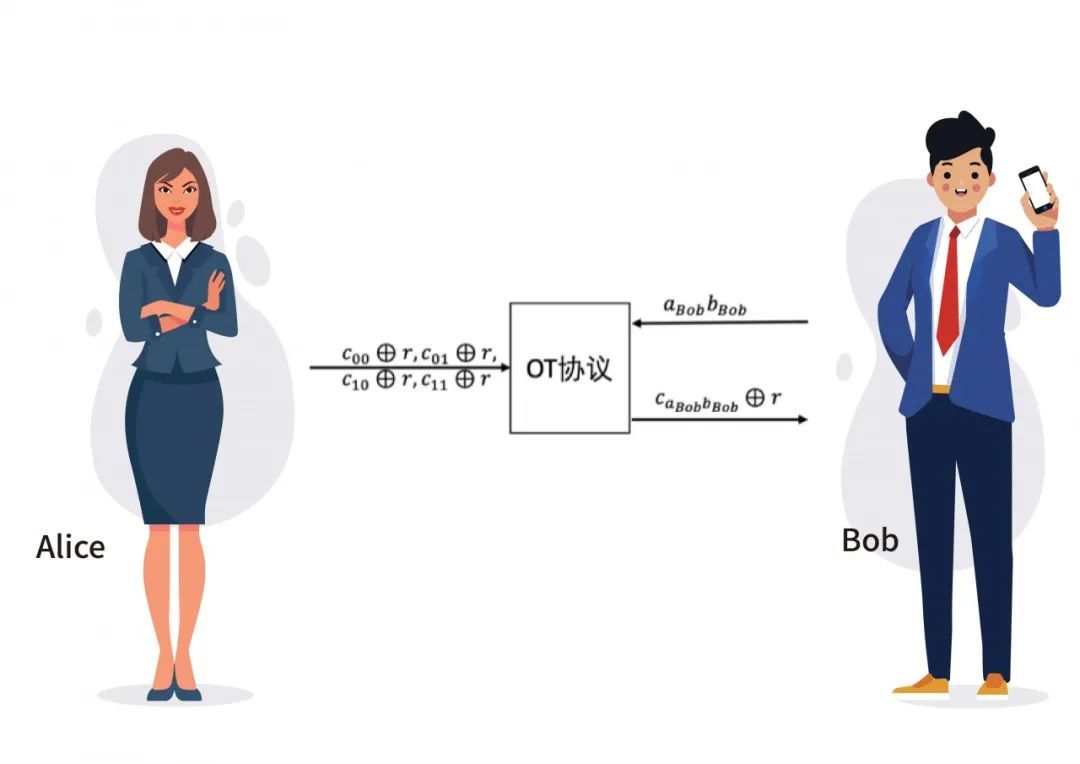
Alice将𝑟作为该与门的输出的子秘密，Bob将𝑐_aBob𝑏Bob⨁𝑟作为该与门的输出的子秘密。

由于Alice和Bob双方间执行的是不经意传输协议，Alice不知道Bob 在𝑐₀₀⨁𝑟, 𝑐₀₁⨁𝑟, 𝑐₀₁⨁𝑟, 𝑐₁₁⨁𝑟中选择了哪个，保证了a_Bob𝑏_Bob依旧对Alice保密。

又由于Alice发送的是𝑟⨁𝑐_aBob𝑏Bob，Bob不知道随机比特𝑟的值，也就不知道𝑐_aBob𝑏Bob的到底是1还是0，只有在最后双方都公布各自手中的计算结果，双方才能合力计算出正确的结果。 

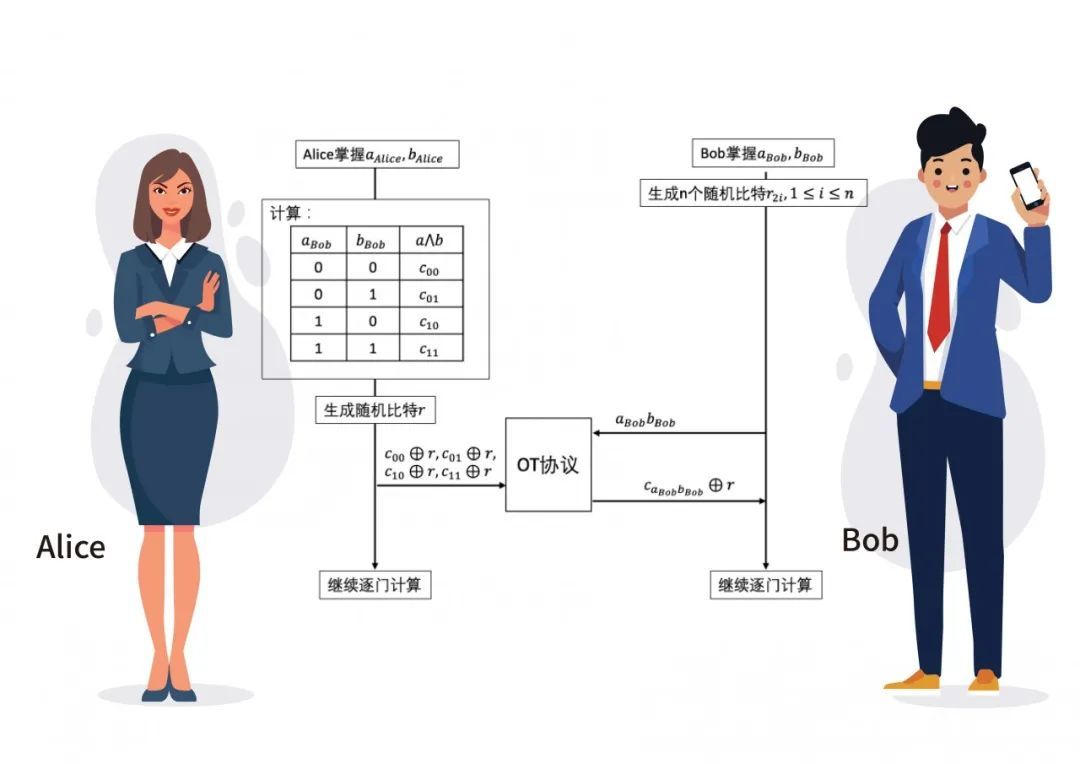
这里Bob得到的子秘密异或上Alice得到的子秘密即为𝑎⋀𝑏的值。 

将GMW协议扩展到多方情况下：参与者为𝑃₁,𝑃₂,…,𝑃_𝑛，假设输入为m个比特，那么每个参与者𝑃_𝑖产生𝑚组，每组𝑛−1个随机比特，分别将每组的𝑛−1个随机比特发送给除了自己之外的n-1个参加者。

假设输入数据为1个比特，那么每个参与者𝑃_𝑖向参与者𝑃_𝑗发送𝑟_𝑖𝑗,1≤𝑗≤𝑛且𝑗≠𝑖。在所有参与者发送完成后，参与者𝑃_𝑖掌握了𝑟_1𝑖,𝑟_2𝑖,…,𝑟_𝑛𝑖。假设𝑃_𝑖的输入为𝑎，那么𝑃_𝑖将𝑎⊕𝑟_1𝑖⊕𝑟_2𝑖⊕…⊕𝑟_𝑛𝑖作为𝑎的子秘密𝑎_𝑖。

对应的收到𝑃_𝑖发送的随机比特𝑟_𝑖𝑗的参与者𝑃_𝑗，将𝑟_𝑖𝑗当做秘密𝑎的子秘密𝑎_𝑗。因此𝑎=𝑎₁⊕𝑎₂⊕…⊕𝑎_𝑛。

对于异或门以及非门，和双方情况下相同，每个参与者直接在本地进行计算即可。对于与门，与门的输入为𝑎和b，参与者𝑃_𝑖手中掌握了𝑎和b的子秘密𝑎_𝑖和𝑏_𝑖，因为𝑎=𝑎₁⊕𝑎₂⊕…⊕𝑎_𝑛，𝑏=𝑏₁⊕𝑏₂⊕…⊕𝑏_𝑛，可得：

这其中，对于𝑃_𝑖来说，每个𝑎_𝑖⋀𝑏_𝑖都可由𝑃_𝑖在本地进行计算。而对于𝑎_𝑖⋀𝑏_𝑗,𝑖≠𝑗，可由参与者𝑃_𝑖和𝑃_𝑗通过上述的两方BGW协议共同计算出𝑎_𝑖⋀𝑏_𝑗的两个子秘密。当电路计算完成，每个参与者公布自己所掌握的子秘密，再将所有的子秘密进行异或，即可得到最后的计算结果。

BGW协议也是支持多方的安全计算协议，BGW协议基于Shamir(t, n)门限秘密共享机制，利用了Shamir秘密共享机制的加法同态和乘法同态的性质。Shamir(t, n)门限秘密共享机制在之前的科普已经进行过介绍了。

假设BGW协议的参与者一共有n人，假设参与者𝑃_𝑖需要输入秘密𝑎，则参与者𝑃_𝑖首先利用Shamir(t,n)门限秘密共享机制将秘密𝑎共享给其他所有参与者，阈值t的选择根据具体使用情景下的安全性要求决定。

当所有参与者的输入都通过Shamir(t, n)门限秘密共享机制分享后，每个参与者都掌握了协议输入的子秘密。假设一个门的输入分别为𝑎和𝑏，秘密𝑎和𝑏已经分别由秘密分配函数

𝑓_𝑎(𝑥) =𝛼_t-1𝑥^t-1+⋯+𝛼₁𝑥¹+𝑎, 𝑓_𝑏(𝑥)=𝛽_t-1𝑥^t-1+⋯+𝛽₁𝑥¹+𝑏

分配完成，𝑓_𝑎(0)=𝑎，𝑓_𝑏(0)=𝑏，参与者𝑃_𝑖掌握𝑎和b的子秘密𝑎_𝑖,𝑏_𝑖。在布尔电路上，可将异或门和与门分别看成在有限域𝐹₂上的加法和乘法。将异或用模为2的加法进行计算，与用模为2的乘法进行计算。

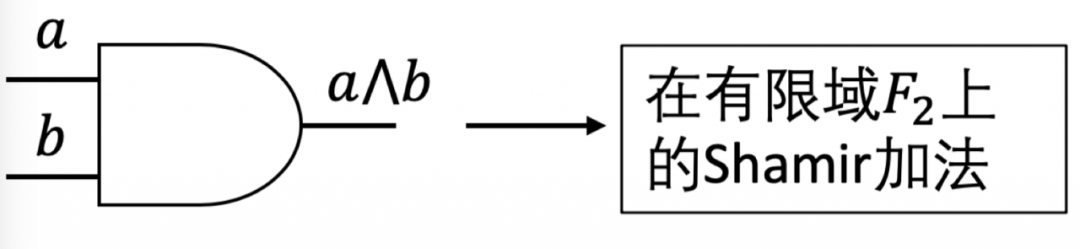
对于异或门：由于Shamir具有加法同态性，因此

𝑎⊕𝑏=𝑓_𝑎(0)⊕𝑓_𝑏(0),𝑓_𝑎(𝑥)⊕𝑓_𝑏(𝑥)=(𝛼_t-1+𝛽_t-1)𝑥^t-1+⋯+(𝛼₁+𝛽₁)𝑥¹+(𝑎+𝑏)

假设𝑓_𝑐(𝑥)=𝑓_𝑎(𝑥)⊕𝑓_𝑏(𝑥)，则𝑓_𝑐(𝑖)=𝑓_𝑎(𝑖)⊕𝑓_𝑏(𝑖)，而𝑓_𝑎(𝑖)=𝑎_𝑖和𝑓_𝑏(𝑖)=𝑏_𝑖都由𝑃_𝑖掌握，因此𝑃_𝑖可以本地计算出𝑓_𝑐(𝑖)=𝑎_𝑖+𝑏_𝑖。当所有计算完成后，每个参与者𝑃_𝑖公布自己计算出的𝑓_𝑐(𝑖)， 即可恢复出𝑓_𝑐(𝑥)和𝑓_𝑐(0)。

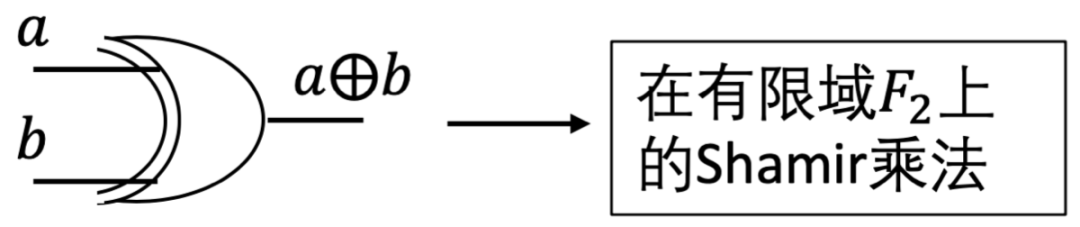
对于与门，和之前叙述过的基于Shamir(t, n)门限共享机制的多方乘法计算相同，只是BGW是在有限域𝐹₂上。每个参与者𝑃_𝑖计算𝑑_𝑖=𝑎_𝑖𝑏_𝑖，接着每个𝑃_𝑖独自选取次数为t次的随机多项式ℎ_𝑖(𝑥)，且满足ℎ_𝑖(0)=𝑑_𝑖,1≤𝑖≤𝑛，𝑡<𝑛/2。

向各个参与者分配𝑑_𝑖，且𝑐_𝑖𝑗= ℎ_𝑖(𝑗),1≤𝑖,𝑗≤𝑛。所有参与者分配结束后，𝑃_𝑖掌握了信息𝑐_1𝑖,𝑐_2𝑖,…,𝑐_𝑛𝑖，同时再利用公开的重组向量𝜆₁,…,𝜆_𝑛，𝑃_𝑖计算𝑐_𝑖=。

此时𝑃_𝑖掌握的子秘密𝑐_𝑖即为𝑎𝑏的子秘密。当所有计算完成后，每个参与者公开自己的子秘密，再根据之前叙述的Shamir(t, n)门限秘密重构算法即可获得𝑎𝑏。