【论文标题】Learning Regularized Positional Encoding for Molecular Prediction
【作者团队】Xiang Gao, Weihao Gao, Wenzhi Xiao, Zhirui Wang, Chong Wang, Liang Xiang
【发表时间】2022/11/23
【机 构】字节跳动
【论文链接】https://arxiv.org/pdf/2211.12773v1.pdf
机器学习已经成为分子建模的一个很有前途的方法。位置相关编码,如原子间距离和键角,在分子物理学中起着关键作用。现有的工作依赖于对其表征的精细设计。为了以更多的端到端方法对预测分子属性的复杂非线性进行建模,本文用连续和可微分的可学习嵌入来编码位置,采用正则化技术来优化沿物理维度的嵌入平稳性。本文对各种分子特性和力场预测任务进行了实验。在插入正则化的位置编码方法后,观察到三种不同的模型结构,EGNN、DimeNet++和Transformer上的性能得到了改善。此外,学习到的位置编码可以更容易地进行基于物理学的解释,另外可以观察到,位置编码也可以和物理学的性质之间有较好的对应。
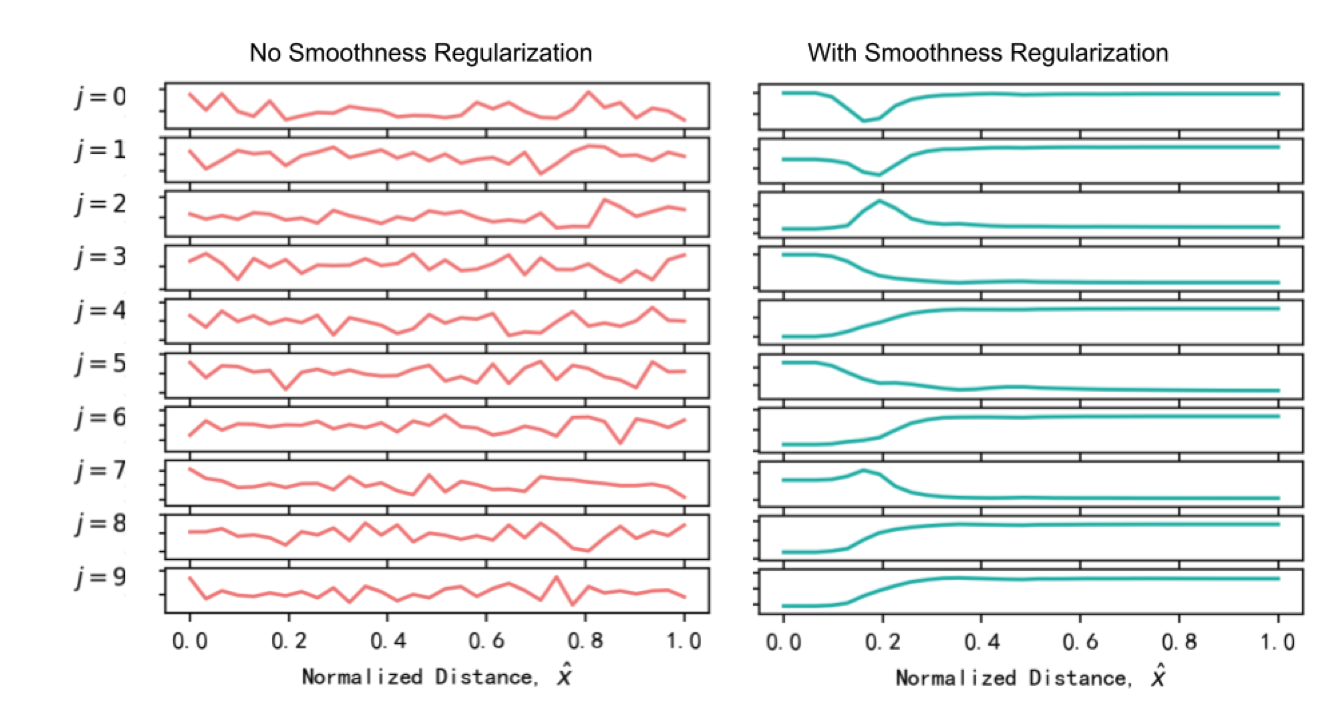
上图展示了平滑正则化对于距离的描述效果的提升,文中也展示了PCA后明显的流形。
与NLP中,离散的位置编码不同是,分子建模的位置编码是连续的。为了用离散点上的嵌入来表示这些连续的物理量,一般将空间划分为n bins,并通过插值最近的bin中心的嵌入来获得任意输入的编码。一个简单的实现方法是通过线性内插,但是这会导致不可导。为了解决这个问题,本文考虑高阶插值,具体选择Cubic Hermite spline(公式见文章,使用了2组需要学习的函数),以这种方式定义的位置编码是连续的,并且相对于x是可微的。
由于位置编码是连续的,本文假设嵌入应该是局部平滑的,两个相邻bin的嵌入之间的差异不应该很大。由此加入一个平滑度损失,定义为一个bin与下一个bin相比的L2正则化计算的平均相对变化,并加权后与原本的损失函数一起形成新的损失函数。这样做虽然减少了位置编码的灵活性,但这可能有助于模型在数据量较小的情况下进行泛化。即使一个bin在训练期间从未被直接训练过(即在训练期间没有x落在这个bin附近),它的参数仍然被更新,因为它与邻居仓的差异被平滑度损失正则化了。
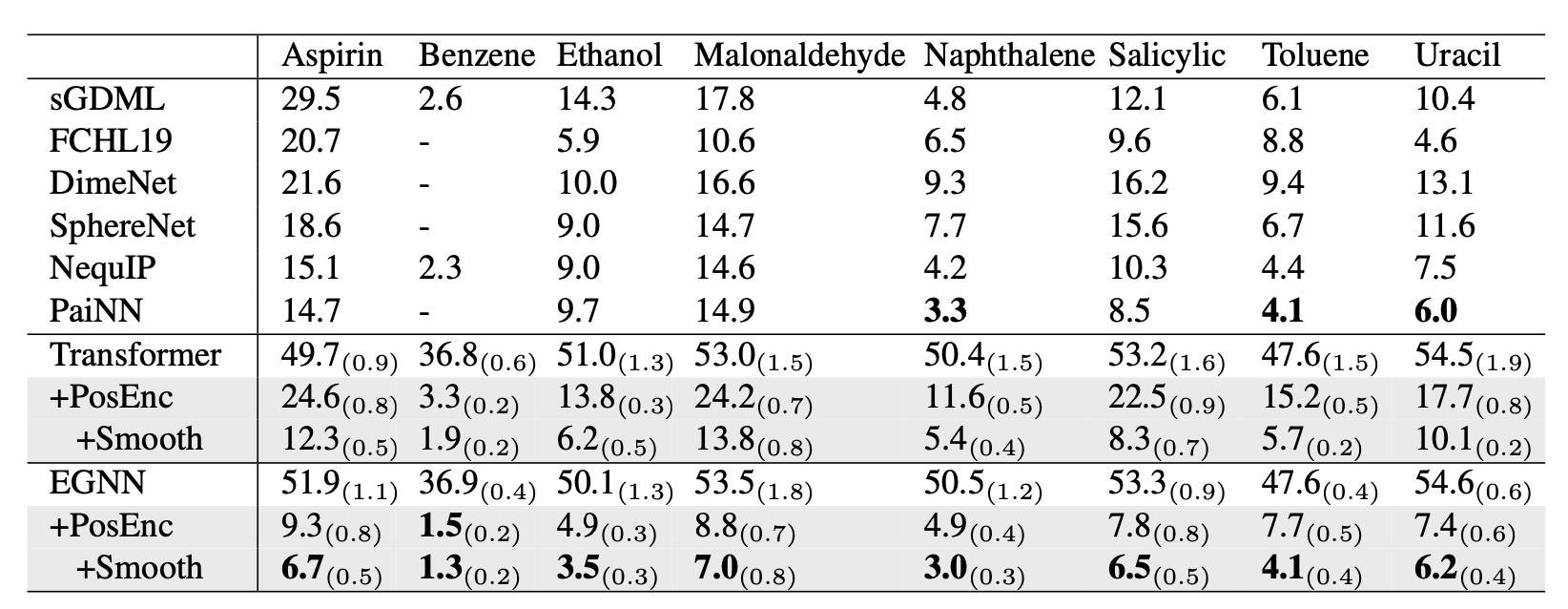
上图展示了本文方法在分子力场数据集MD17上的表现(MAE),任务目标是预测在分子的三维几何结构下作用于每个原子的力。
一般的EGNN和基于Transformer的模型在这个任务傻姑娘都显示出很大的误差,尽管这两个架构之前在各种任务中取得了成功。这可能是因为该任务的数据特征使得EGNN和基于Transformer的模型对原子间距离的相对简单的编码在这个任务中表现不佳。分子力场对三维几何形状的变化非常敏感。在MD17数据集中,同一分子的三维几何形状彼此之间只有微小的差别,而作用在原子上的力在不同的分子构型中却有很大的变化。然而在使用了本文的位置编码方法(+PosEnc)来表示原子间距离后大大减少了EGNN和基于Transformer的模型的测试误差。当采用建议的平滑度正则化技术(+Smooth)时,测试误差进一步减少。

上图展示了学到的嵌入在各种物理性质任务、多项式基线之间的在单调性、多样性等4方面表现。一些关键属性包括:μ:dipole moment,R2: electronic spatial extent,U:298.15 K internal energy,U0:0 K internal energy,H:enthalpy,G:free energy,ZPVE:zero point vibrational energy,α:isotropic polarizability、和∆ε:energy gap。在某些任务中,学习到的嵌入的平滑度接近于多项式嵌入。这表明本文位置编码方法学习到的嵌入包含非线性或非单调的性质,但仍保持平滑。
本文还在尝试将嵌入和多种物理性质对应:
1.可以反映了不同任务对短距离和长距离的物理依赖,比如对于U0和H,当距离大于某些 "截止 "值时,嵌入值不会有太大变化。这与问题的物理性质一致。QM9中考虑的系统的U0和H通常由短程相互作用主导,在这些系统中没有明显的长程力,如静电力。
2.学习距离嵌入的非单调性是源于任务的物理性质,内能与作用于原子的势力有关。力可以是非单调性的,与距离有关。短距离往往被排斥力所支配,而吸引力在大距离上更显著,与这种非单调性物理学相一致。
3.物理性质相似的任务有相似的嵌入,能量U、U0、H、G和ZPVE之间显示出高度的相似性(≥ 0.88)。另一组物理量α、μ和∆ε与分子的反应性密切相关。这一组的配对嵌入相似度很高(≥0.90),相比之下,这两组之间的交叉相似性相对较低。
创新点
1. 本文提出了一种可学习的位置编码方法,它是连续的和可微分的。该方法可用于表示原子间距离、键角和其他具有一系列非线性变换的位置量。实验表明,用这种技术可以取得最先进的新结果。
2. 本文为所提出的位置编码提出了一种正则化方法。基于物理直觉,该方法使嵌入形成一个有意义的流形,以便从物理的角度更容易进行可视化和解释。正则化减少了过拟合,可以进一步提高某些任务的模型精度。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢