导读
一直以来,对于 Heatmap-based 方法的改进工作层出不穷,我过去也介绍了不少轻量且高效的算法,而这一篇相对来说不太一样,算法的训练速度会变慢一些,不过在我看来却是对 Pose 和 Detection 方法的进一步拉近。
总体而言,本文的工作就是证明了最优传输分配(Optimal Transport Assignment, OTA)方法在姿态估计任务中同样有效。
如果读者对目标检测领域近年的文章有一些了解的话,会明白最近的很多算法都离不开一个叫做动态标签分配(Dynamic Label Assignment)的东西,简单来说,一个 Detection 任务里,模型预测了 N 个结果,而图里有 M 个标注框,那么在计算 Loss 时就会面临一个匹配问题,或者说,每个结果应该“向谁学”的问题。
传统的分配策略一般是静态的,基于一些人工先验,比如当前的像素落在哪个 GT 框里,或者距离哪个 GT 框的中心最近,那么这个像素的预测结果就向那个 GT 学习(跟它计算 Loss)。
静态分配略显死板,在一些复杂的场景,物体相互遮挡堆叠在一起,这种基于朴素先验的分配策略就不一定是最优的了,于是有研究者提出了用 OTA 算法来动态分配。
讲到 OTA 就不得不提我们的推土机距离(Earth Mover Distance, EMD)了,它有另一个比较响亮的名字,叫 Wasserstein 距离,没错就是之前随着 GAN 一起走红的那个。
EMD 有一个非常形象的比喻,就是把 N 个不同重量的土堆,运到 M 个地方,每个地方运不同分量,完成这个任务所需要的最小的开销。
在上面这个描述里,N 个土堆,每个土堆的重量,以及搬运土堆所需要的开销都是已知量,核心目标是给出一个搬运方案,“从 a 土堆搬运 x 份土到 b 点, 搬运 y 份土到c 点…”,不难想到,这样的一份搬运计划最终可以用一个 NxM 的矩阵来表示,并且一定会存在一个最优的搬运方案是开销最小的,于是按照线性规划求解即可。
于是可以这样说,我们的核心诉求其实是计算出一个 NxM 的 Cost Matrix,然后根据这个矩阵来完成 N 到 M 的匹配。由于训练中参数不断更新,模型的预测结果也随之改变,因此这个分配是动态的,当这个 Cost Matrix 中的开销是用损失函数公式(并不是只能用这个)来计算时,相当于模型可以根据自己当前的状态,动态地选择最合适的目标去学习。
OK, 简单科普完 OTA 和 EMD,那么这个东西如何用到姿态估计任务里呢?
方法
1. Gaussian Heatmap 监督的问题
这里得先再把 Gaussian Heatmap 监督方法拿出来批判一番。过去我们的标准做法是人工渲染一张二维高斯分布热图,然后模型也预测一张热图,两张图计算 MSE Loss。
而问题就出在 MSE 上,作为一个非常经典的 Loss,在 Heatmap 这种密集预测任务上实际上是存在问题的,当 Loss 降低时,并不一定模型的预测结果会变好。
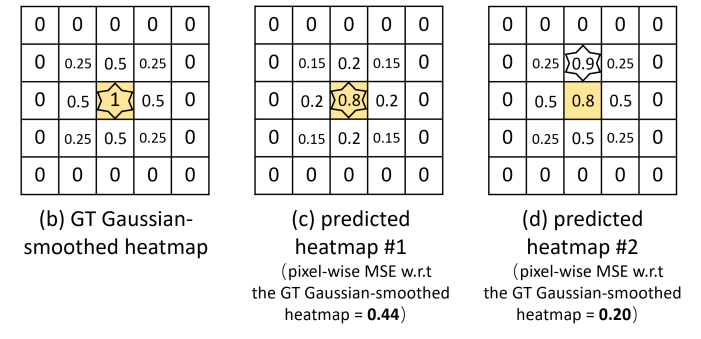
上图是一个典型的例子,对于人工渲染的高斯热图(b)而言,预测结果©能通过 Argmax 解码得到准确的定位,而(d)则出现了偏差,显然©是更符合我们期待的结果,但 MSE 计算出来的损失值却是(d)更小,所以模型训练优化时会认为(d)是更好的。
究其原因,在于 MSE 是一种逐像素的对位监督,每个预测像素都只关心自己能不能正确预测对应位置的 GT 值,这跟我们的核心诉求“准确预测关键点定位”之间是存在一定的 gap 的,虽然大方向上存在正相关性,但并不完全一致,所以需要我们对 Loss 进行优化,选择一种更符合我们核心诉求的损失函数。
2. 损失函数的问题
如果把关键点位置表针的热图看成离散概率分布的话,很自然地能想到用 KL 散度作为损失函数,关于 KL 散度这里不做过多的介绍了,感兴趣的小伙伴可以自行查阅一下资料,简单来说 KL 散度能够衡量两个概率分布的相似程度,在分类中最常见的交叉熵实际上就是 KL 散度公式的一部分。
\( D_{\text{KL}}(q(x) || p(x)) = \mathbb{E}_{q(x)} \log [q(x) / p(x)] \)
尽管 KL 散度可以描述两个分布的相似度,但它并不是一种距离,因为 KL 散度是不对称的,KL(p, q) 和 KL(q, p) 的含义和结果都是不同的,因此不能视为一种距离,于是大家常常使用具有对称性的 JS 散度作为损失函数,往往能取得比 KL 散度略好的效果。
\( m=\frac{p(x) + q(x)}{2} \)
\( D_{\text{JS}}(p(x)| q(x)) = \frac{D_{\text{KL}}(p(x)|m) + D_{\text{KL}}(q(x)|m)}{2} \)
然而, JS 散度和 KL 散度都有一个共同的缺陷,当两个分布没有任何重叠时,不论分布怎么移动,两种损失计算结果都为0,因此不能很好地度量分布相似度。
于是后来有人引入了 Wasserstein 距离来更好地衡量分布相似度,根据前面的介绍可以看出,由于 Wasserstein 距离并不是每个位置对应比较,而是 m 到 n 的全匹配,这种匹配是位置无关的,因此即使两个分布没有任何重叠,依然可以计算出不同的损失值。
3. 监督信号
在监督信号方面,传统的人工渲染 Gaussian Heatmap 的方式是非常不合理的,对于所有图片都使用相同的 sigma 渲染,于是本文使用了更简单的监督信号,通过插值的方式直接将连续空间上的坐标用相邻的离散像素计算表示。
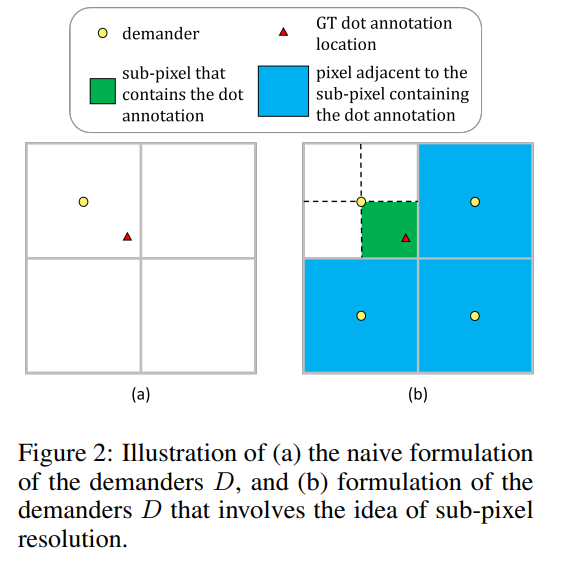
具体而言,对于二维空间上的标注点(红色三角),可以表示为周围最近的四个像素采样点上的权重与它到四个点距离的加权和:
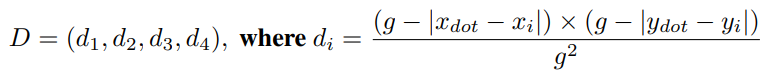
这样就可以把单个的坐标值转化为二维离散空间上的概率分布了。
最终训练的时候,直接用 Wasserstein 当 Loss 计算会非常缓慢,不过之前也早有研究者提出了近似算法 Sinkhorn,能够通过多步迭代得到近似的 Wasserstein,目前也已经有开源的基于 torch 的版本可以用。感兴趣的小伙伴可以自行了解一下。
实验
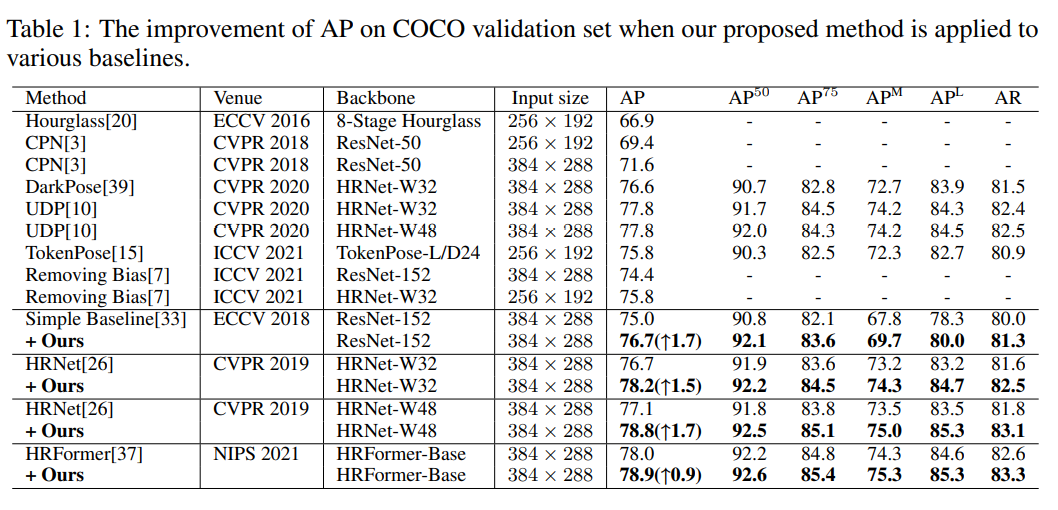
可以看到在较大的输入尺寸(384x288)上的提升还是比较明显的,在大模型上普遍能有1个点以上的提升,不过论文里没有给256x192的精度。
由于抛弃了人工渲染 Gaussian Heatmap,模型预测的结果也有所改变,不再是非常大的一片区域,而是非常凝聚的接近于一个点。

个人感觉这篇文章的价值在于进一步拉近了 Pose 和 Det 的距离,事实上我也一直觉得 Det 近年的很多技术是领先于 Pose 且可以迁移过来使用的,相信这篇工作也会很快像 OTA 之于 SimOTA/TOOD 等工作一样,启发 Pose 领域快速迭代出更多更高效的动态匹配算法。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢