机器学习数学本质的理解

近日，国际数学家大会丨鄂维南院士作一小时大会报告：从数学角度，理解机器学习的“黑魔法”，并应用于更广泛的科学问题。

鄂维南院士在2022年的国际数学家大会上作一小时大会报告(plenary talk)。

今天我们带来鄂老师演讲内容的分享。

鄂老师首先分享了他对机器学习数学本质的理解（函数逼近、概率分布的逼近与采样、Bellman方程的求解）；

然后介绍了机器学习模型的逼近误差、泛化性质以及训练等方面的数学理论；

最后介绍如何利用机器学习来求解困难的科学计算和科学问题，即AI for science。

机器学习问题的数学本质

众所周知，机器学习的发展，已经彻底改变了人们对人工智能的认识。机器学习有很多令人叹为观止的成就，例如：

比人类更准确地识别图片：利用一组有标记的图片，机器学习算法可以准确地识别图片的类别：

Cifar-10 问题：把图片分成十个类别

来源：https://www.cs.toronto.edu/~kriz/cifar.html

Alphago下围棋打败人类：完全由机器学习实现下围棋的算法：

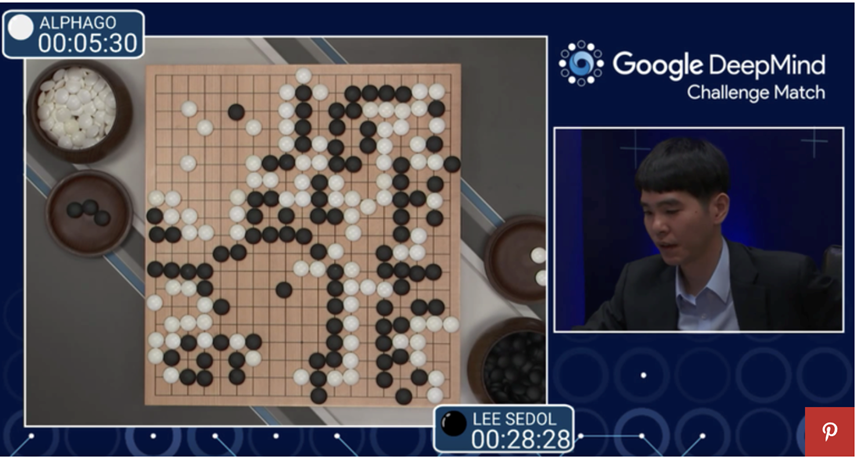
参考：https://www.bbc.com/news/technology-35761246

产生人脸图片，达到以假乱真的效果：

参考：https://arxiv.org/pdf/1710.10196v3.pdf

机器学习还有很多其他的应用。在日常生活中，人们甚至常常使用了机器学习所提供的服务而不自知，例如：我们的邮件系统里的垃圾邮件过滤、我们的车和手机里的语音识别、我们手机里的指纹解锁……

所有这些了不起的成就，本质上，却是成功求解了一些经典的数学问题。

对于图像分类问题，我们感兴趣的其实是函数：

: 图像→类别

函数把图像映射到该图像所属的类别。我们知道在训练集上的取值，想由此找到对函数的一个足够好的逼近。

一般而言，监督学习(supervised learning)问题，本质都是想基于一个有限的训练集S，给出目标函数的一个高效逼近。

对于人脸生成问题，其本质是逼近并采样一个未知的概率分布。在这一问题中，“人脸”是随机变量，而我们不知道它的概率分布。然而，我们有“人脸”的样本：数量巨大的人脸照片。我们便利用这些样本，近似得到“人脸”的概率分布，并由此产生新的样本（即生成人脸）。

一般而言，无监督学习本质就是利用有限样本，逼近并采样问题背后未知的概率分布。

对于下围棋的Alphago来说，如果给定了对手的策略，围棋的动力学是一个动态规划问题的解。其最优策略满足Bellman方程。因而Alphago的本质便是求解Bellman方程。

一般而言，强化学习本质上就是求解马尔可夫过程的最优策略。

然而，这些问题都是计算数学领域的经典问题！！毕竟，函数逼近、概率分布的逼近与采样，以及微分方程和差分方程的数值求解，都是计算数学领域极其经典的问题。那么，这些问题在机器学习的语境下，到底和在经典的计算数学里有什么区别呢？答案便是：维度（dimensionality）。

例如，在图像识别问题中，输入的维度为。而对于经典的数值逼近方法，对于维问题，含个参数的模型的逼近误差. 换言之，如果想将误差缩小10倍，参数个数需要增加. 当维数增加时，计算代价呈指数级增长。这种现象通常被称为：维度灾难（curse of dimensionality）。

所有的经典算法，例如多项式逼近、小波逼近，都饱受维度灾难之害。很明显，机器学习的成功告诉我们，在高维问题中，深度神经网络的表现比经典算法好很多。然而，这种“成功”是怎么做到的呢？为什么在高维问题中，其他方法都不行，但深度神经网络取得了前所未有的成功呢？

从数学出发，理解机器学习的“黑魔法”：监督学习的数学理论

2.1 记号与设定

神经网络是一类特殊的函数。比如，两层神经网络是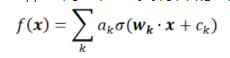

其中有两组参数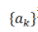，和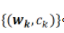。是激活函数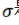，可以是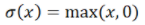： ，ReLU函数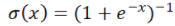；Sigmoid函数。而神经网络的基本组成部分即为：线性变换与一维非线性变换。深度神经网络，一般就是如下结构的复合：

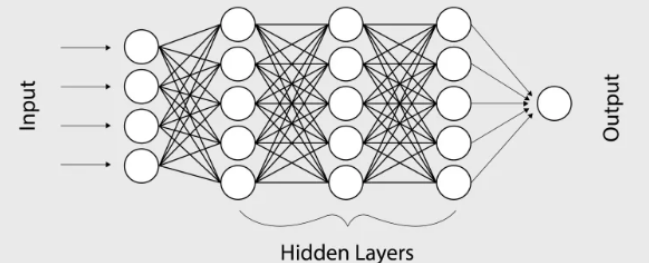
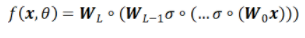
为了简便，我们在此省略掉所有的bias项。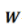是权重矩阵，激活函数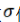作用在每一个分量上。

我们将要在训练集S上逼近目标函数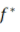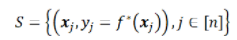不妨假设X的定义域为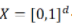。令为x的分布。那么我们的目标便是：最小化测试误差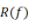(testing error，也称为population risk或generalization error)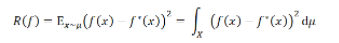

内容中包含的图片若涉及版权问题，请及时与我们联系删除