Beaver三元组

Beaver三元组（Beaver Triple）主要用于安全多方计算协议中的乘法计算。它的应用范围为加法和乘法均为线性的秘密分享机制。

 

用[∗]表示秘密被分享之后的状态，如[𝑎]表示秘密𝑎已经通过秘密分享函数被分享给了参与者，如果有n个参与者，则[𝑎] = {𝑎1,𝑎2,…,𝑎𝑛}。假设秘密共享函数为𝑓(𝑥)，𝑥为待共享的秘密，参与者为𝑃1,𝑃2,…,𝑃𝑛，参与者𝑃𝑖拿到的𝑥的子秘密记为𝑥𝑖。

假设需要分享的秘密为𝑎、𝑏，参与者𝑃𝑖获得的𝑎、𝑏的子秘密为𝑎𝑖、𝑏𝑖。

加法秘密分享机制为线性的意思为：存在一组常数𝜆1, 𝜆2,…,𝜆𝑛，使得：

将其抽象简记为：

乘法秘密分享机制为线性的意思为：存在一组常数𝜆1, 𝜆2,…,𝜆𝑛，使得：

将其抽象简记为：

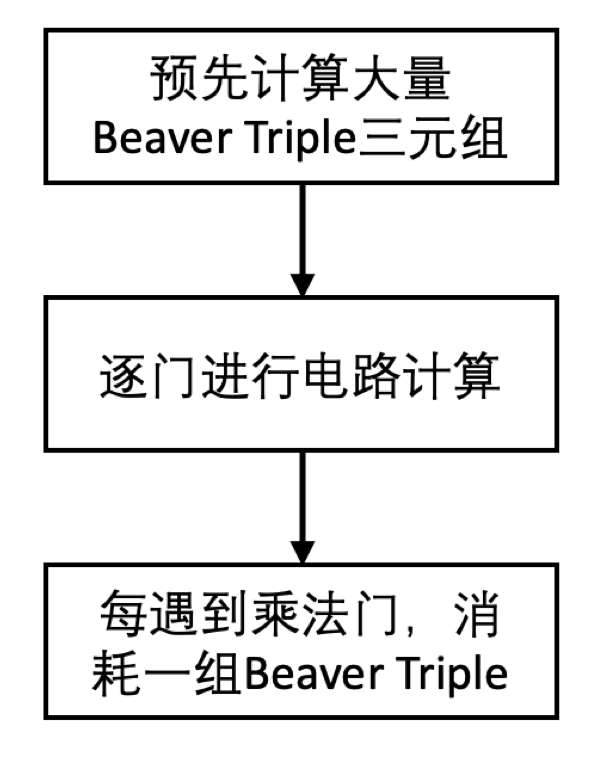
Beaver Multiplication的主要流程为：

在协议开始之前预先产生一个随机三元组：

其中𝑎和𝑏对所有参与者保密，𝑐满足𝑐=𝑎∙𝑏。假设秘密𝑥和𝑦已经被分享，现在需要计算 [𝑥𝑦] 。

1. 所有参与者公开 [𝛼],[𝛼]=[𝑥]−[𝑎]

2. 所有参与者公开 [𝛽],[𝛽] = [𝑦]−[𝑏]

3. 所有参与者计算 [𝑧]=[𝑐]+𝛼∙[𝑏]+𝛽∙[𝑎]+𝛼∙𝛽

因为 [𝛼] 和 [𝛽] 已公开，因此所有参与者都可以通过秘密重构函数独立计算出𝛼和𝛽。又因为：

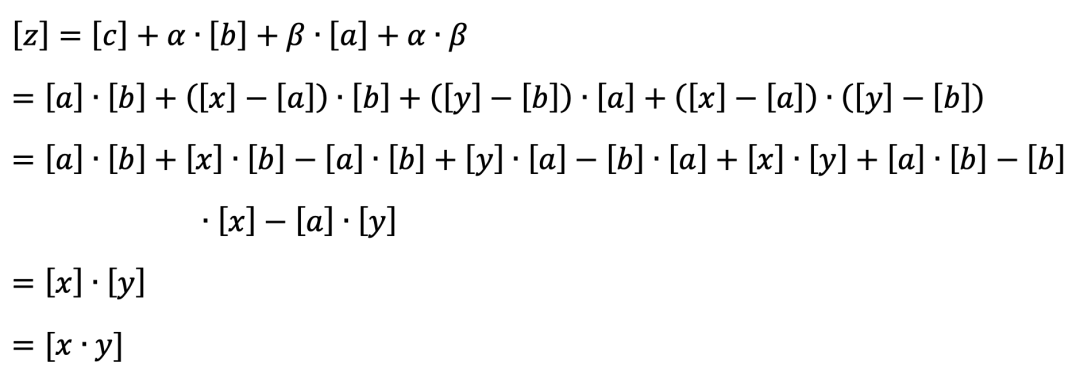
由于[𝑎],[𝑏],[𝑐]是预先产生和分配的三元组，因此在乘法计算时参与者只需要本地计算[𝛼]=[𝑥]−[𝑎]和[𝛽]=[𝑦]−[𝑏]，并对计算结果[𝛼]和[𝛽]进行公开。

而对于上次叙述的BGW协议，在计算乘法时，需要每一个参与者计算[𝑎]∙[𝑏]，之后对[𝑎]∙[𝑏]进行秘密共享，将子秘密分别发送给其他所有参与者。

Beaver三元组是消耗性，每次乘法计算都会消耗一个Beaver三元组，通过预先计算的Beaver三元组，将通信量和计算量移到了协议开始之前。 

 

BMR协议
之前介绍的姚氏混淆电路只支持双方计算，BMR（Beaver-Micali-Rogaway）协议将姚氏混淆电路扩充到了多方情景。

混淆电路的加密由一方对每条导线的真实输入值生成一个随机加密值，并根据每个门的真值表生成对应的加密表来实现。

因此如果直接把混淆电路协议扩展到多方，由一方对整个电路进行加密，或者对电路的一部分门进行加密，那么当加密方与参与者中的某个求值方进行串通或者这两者的信息都被收买时，就会破坏协议的安全性。

为了安全性，需要让所有参与者共同生成所有导线的加密值和门的加密真值表。

具体而言，需要每个参加者随机生成每条导线的加密值，之后将自己生成的加密值进行掩盖后提交到多方计算协议，协议将每个参与者提交的关于同一条导线加密值进行异或，得到多方协同生成的布尔电路中该条导线的加密值。

BMR协议具体如下：

首先协议根据需要实现的目标函数生成布尔电路𝒞，并向所有参与者公开。将电路𝒞中的各条导线分别标记为𝑤1,𝑤2,…,𝑤t。协议参与者为𝑃1,𝑃2,…,𝑃𝑛，其输入分别为𝑥1,𝑥2,…,𝑥𝑛∈ {0,1}。

对于电路𝒞中的每一条导线𝑤𝑖，参与者𝑃𝑗随机产生导线𝑤𝑖 的真值 0，1对应的随机值，分别记为

满足，即为𝑙比特的随机比特串，为1比特的随机比特。再产生一个随机翻转比特𝑓𝑖,𝑗∈{0,1}。对于每一条导线，参与者𝑃𝑖计算

因为, 因此只需要发送或者就可。函数𝐹()可看作是哈希函数，其将𝑙位的输入扩展为𝑛∙(𝑙+1)位，𝑛是参与者数量。

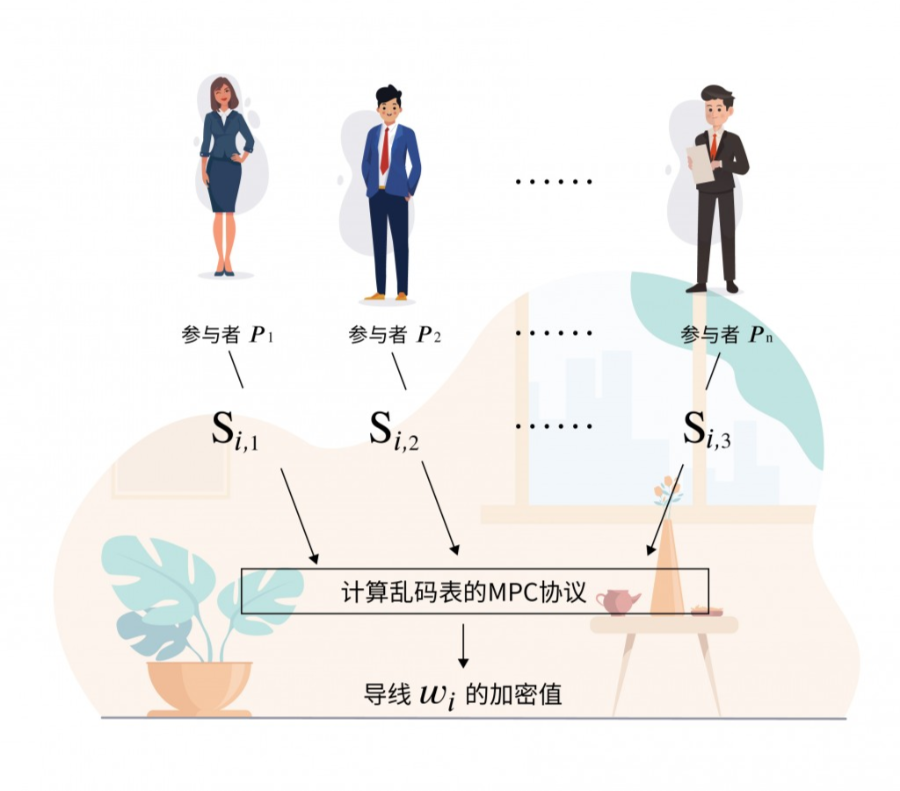
对于布尔电路𝒞中的每一个门𝐺𝑖，所有参与者共同参与一个计算乱码表的多方安全计算协议。该协议的输入是每个参与者之前计算的𝑆𝑖,𝑗和参与者的输入 𝑥1,𝑥2,…,𝑥𝑛。该协议的目标为：

假设电路𝒞中门𝐺𝑖的输入导线为𝑤𝑎, 𝑤𝑏，输出导线为𝑤𝑐。门𝐺𝑖实现的函数为𝑤𝑐= 𝑔(𝑤𝑎,𝑤𝑏)。 

计算指针比特：

并设置：

同理，对所有参加者提交的翻转比特求异或，

得到翻转比特𝑓𝑎,𝑓𝑏,𝑓𝑐，翻转比特用于掩盖参与者𝑃𝑖的输入，使得𝑃𝑖无法得知其对每条导线加密值的具体贡献。 

接着创建门𝐺𝑖的乱码表，让𝑣𝑎, 𝑣𝑏分别是导线𝑤𝑎, 𝑤𝑏, 的输入，对于𝐺𝑖输入𝑣𝑎,𝑣𝑏∈{0,1}，一共只有四种可能的组合。

让𝑣𝑐是导线𝑤𝑐的真实输出值，𝑒𝑣𝑎,𝑣𝑏是导线𝑤𝑐的加密值。设定

即𝑒𝑣𝑎,𝑣𝑏共有四个可能的值，如下表所示：

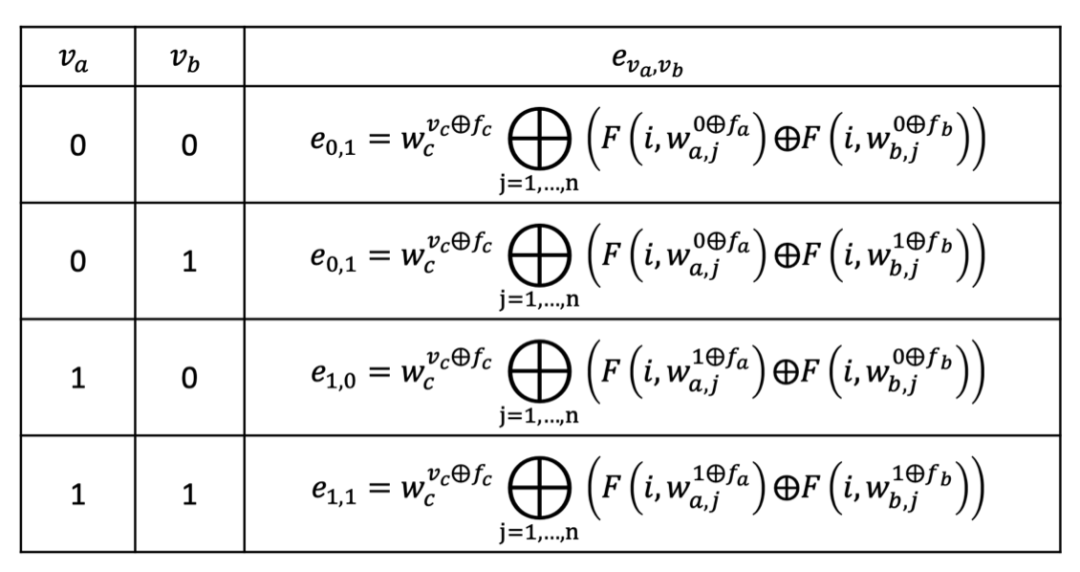
其中，即将各个和, 进行级联。之后对乱码表中𝑒𝑣𝑎,𝑣𝑏的条目进行重新排序，并将条目𝑒𝑣𝑎,𝑣𝑏放在的位置上。 

向参与者𝑃1输出计算得到的乱码表，向𝑃1发送各个参与方的输入𝑥1,𝑥2,…,𝑥𝑛所对应的电路𝒞的加密导线值。

 

 

内容中包含的图片若涉及版权问题，请及时与我们联系删除