©作者 | Qun
前言
数据类别不均衡是很多场景任务下会遇到的一种问题。比如 NLP 中的命名实体识别 NER,文本中许多都是某一种或者几种类型的实体,比如无需识别的不重要实体;又或者常见的分类任务,大部分数据的标签都是某几类。
而我们又无法直接排除这些很少的类别的数据,因为这些类别也很重要,仍然需要模型去预测这些类别
数据采样
有时会从数据层面缓解这种类别不均衡带来的影响,主要是过采样和欠采样。
-
过采样:对于某些类别数据比较少,对它们进行重复采样,以达到相对平衡,重复采样的时候,有时也会对数据加上一点噪声;
-
欠采样:对于某些类别数据特别多,只使用部分数据,抛弃一些数据;
过采样可能导致这些类别产生过拟合的现象,而欠采样则容易导致模型的泛化性变差。
另外,比较常用的则是结合 ensemble 方法,则将数据切分为 N 部分,每部分都包含数据少的类别的所有样本和数据多的类别的部分样本,训练 N 个模型,最后进行集成。
缺点是,使用 ensemble 则会提高部署成本和带来性能问题。
损失函数
如果在损失函数方面下功夫,针对这种类别不均衡的场景设计一种 loss,能够兼顾数据少的类别,这其实是一种更理想的做法,因为不会破坏原数据的分布,并且不会带来性能问题(对训练速度可能有轻微的影响,但不影响推理速度)。
下面,我们就介绍在这方面几种常用的 loss 设计。
Focal Loss
Focal Loss 是一种专门为类别不均衡设计的loss,在《Focal Loss for Dense Object Detection》这篇论文中被提出来,应用到了目标检测任务的训练中,但其实这是一种无关特定领域的思想,可以应用到任何类别不均衡的数据中。
首先,还是从二分类的cross entropy(CE)loss入手:
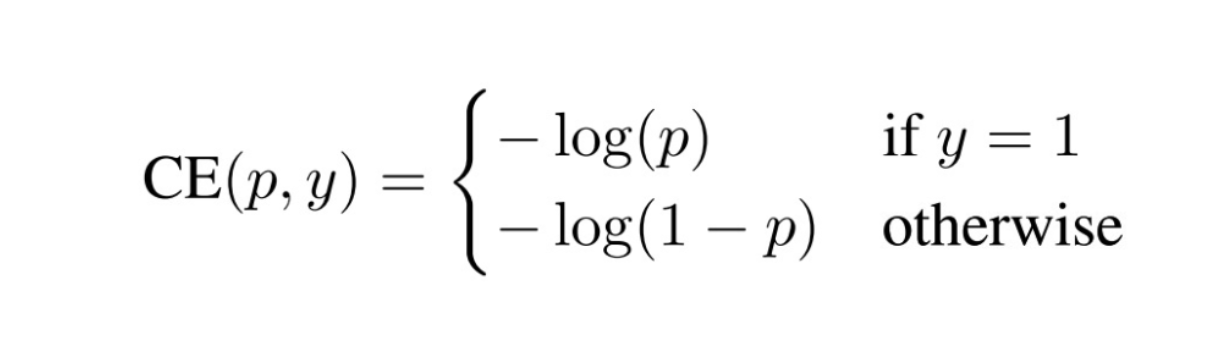
为了符号的方便,![]()
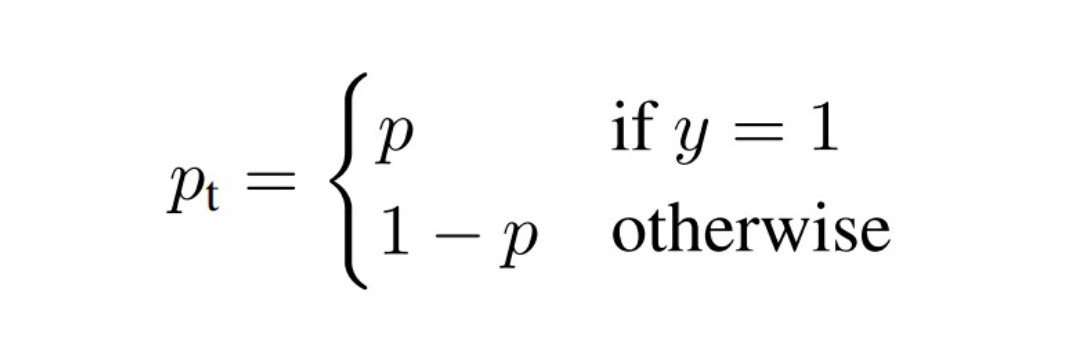
4.1 问题分析
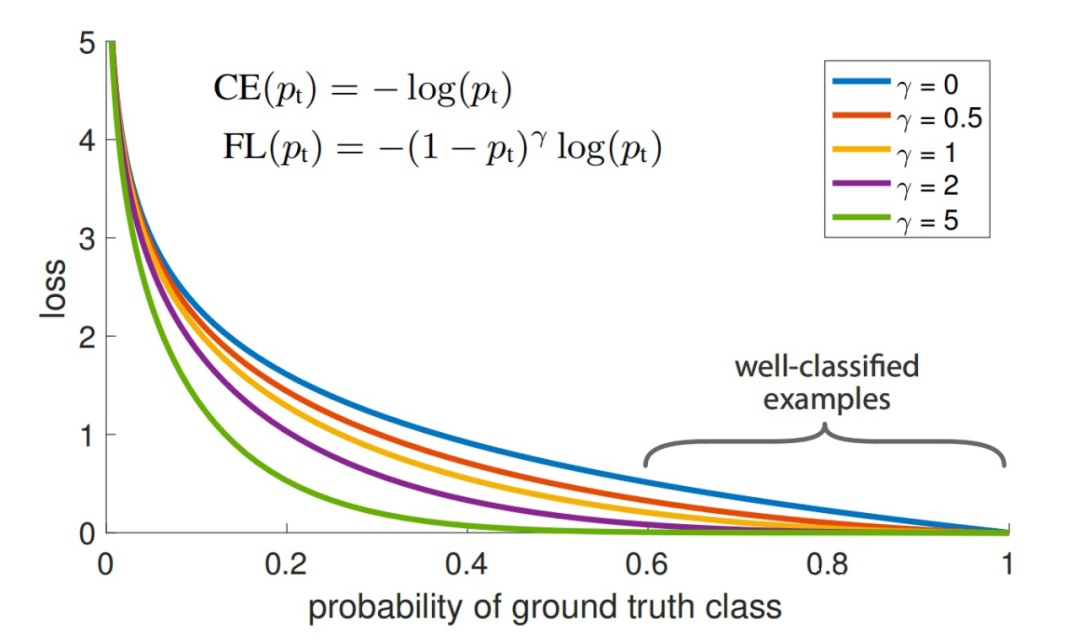
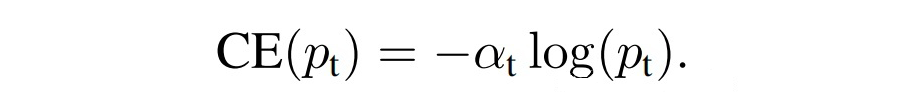
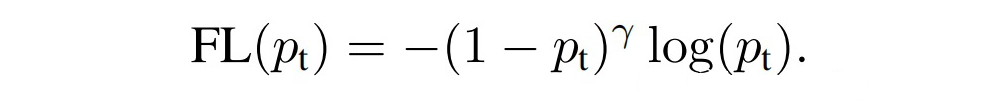
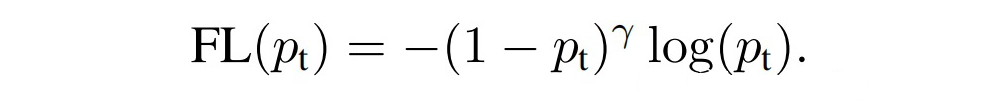
GHM(Gradient Harmonizing Mechanism)
梯度调和机制 Gradient Harmonizing Mechanism 的设计目的也是为了解决不均衡类别的问题而对 loss 函数进行优化,出自《Gradient Harmonized Single-stage Detector》。
5.1 介绍
GHM 同样表述了关于容易样本和困难样本的观点 A:模型从容易分类的样本的到收益很少,模型应该关注那些困难分类的样本,不管它属于哪一种类别,但大量的容易样本加起来的贡献会盖过困难样本,使得训练效益很低;
进一步指出 Focal Loss 的问题,提出不同的观点 B:
1. Focal Loss 存在两个超参数,并且是互相影响,构成许多参数组合,会导致调参需要很多尝试成本;并且,Focal Loss 是一种静态的 loss,那么同一种超参数无法适用于不同的数据分布;
2. 有一些特别困难分类的样本,它们很可能是离群点,加入这些样本的训练,会影响模型的稳定性;
3. 提出了 gradient density(梯度密度)的梯度调和机制,来缓解这种类别不均衡的问题。
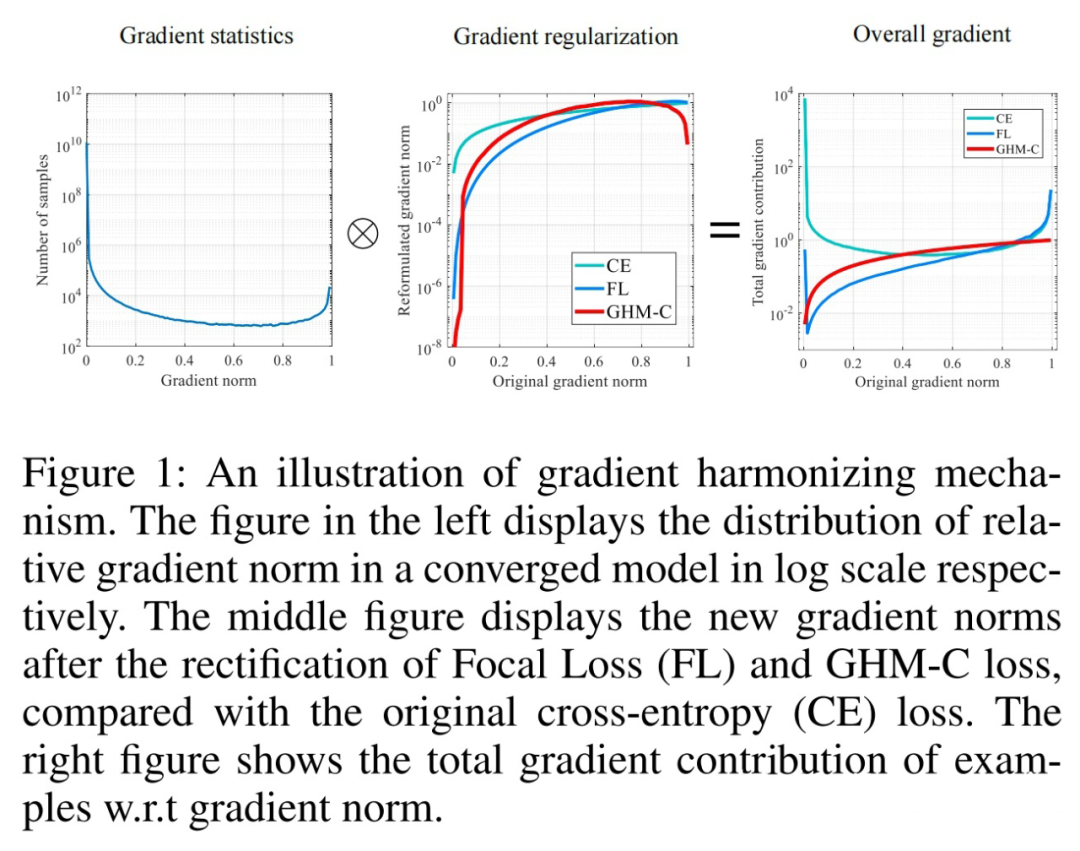
下图左展示了上述观点 A,梯度范数 gradient norm 的大小则代表样本的分类难易程度,收益实际即对应为梯度;
下图中和右展示了通过 GHM 的梯度调和之后,容易样本的 gradient norm 会被削弱许多,并且特别困难的样本也会被轻微削弱,分别对应观点 A 和观点 B-2 的解决方案。
5.2 理论
基于这些分析,论文提出了一种梯度调和机制 GHM(Gradient Harmonizing Mechanism),其主要思想是:首先仍然是降权大量容易样本贡献的梯度总和,其次是对于那些特别困难样本即离群点,也应当相对地降权。
为了解决这种 gradient norm 的分布问题,论文提出了一种调和手段:Gradient Density
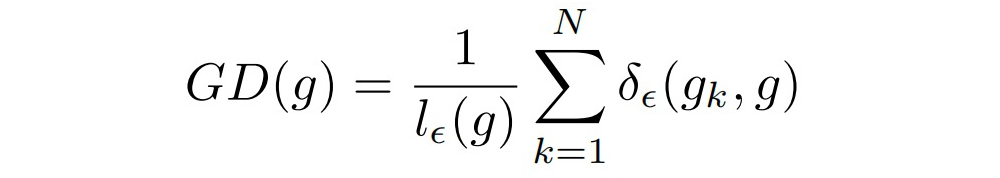
其中, 为第 k 个样本的 gradient norm。g 的梯度密度即 表示落于以 g 为中心,长度为 的中心区域的样本数量,然后除以有效长度进行标准化。
那么,梯度密度调和参数为:N 为样本数量。
可以看作是梯度上在第 i 个样本周边样本频率的一种正则化:
1. 如果所有样本的梯度是均匀分布的,那么对于每个样本 i:,意味着每个样本都没起到任何改变;
2. 见上图 2,容易样本的频率很高,那么 就会变得很小,起到降低这些样本的权重的效果;并且特别困难样本即离群点的频率会比中等困难的样本频率多,意味着这些离群点的 会相对较小,那么也会相对地轻微降低这些样本的权重;
3. 从第 2 点可以看出,GHM 其实只适用于那些容易样本和特别困难样本的数量比中等困难样本多的场景。
5.3 计算优化
代码实现
tensorflow 及 torch 的实现:github:
https://github.com/QunBB/DeepLearning/tree/main/Trick/unbalance
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢