物理嵌入神经算子应用

来自今天的爱可可AI前沿推介

[LG] Applications of physics informed neural operators

S G. Rosofsky, H A Majed, E. A. Huerta
[Argonne National Laboratory]

物理嵌入神经算子应用

简介：提出一种端到端框架来学习偏微分方程，结合了初始数据生成、边界条件选择和物理嵌入神经算子来求解从简单方程到更复杂的方程和耦合偏微分方程。

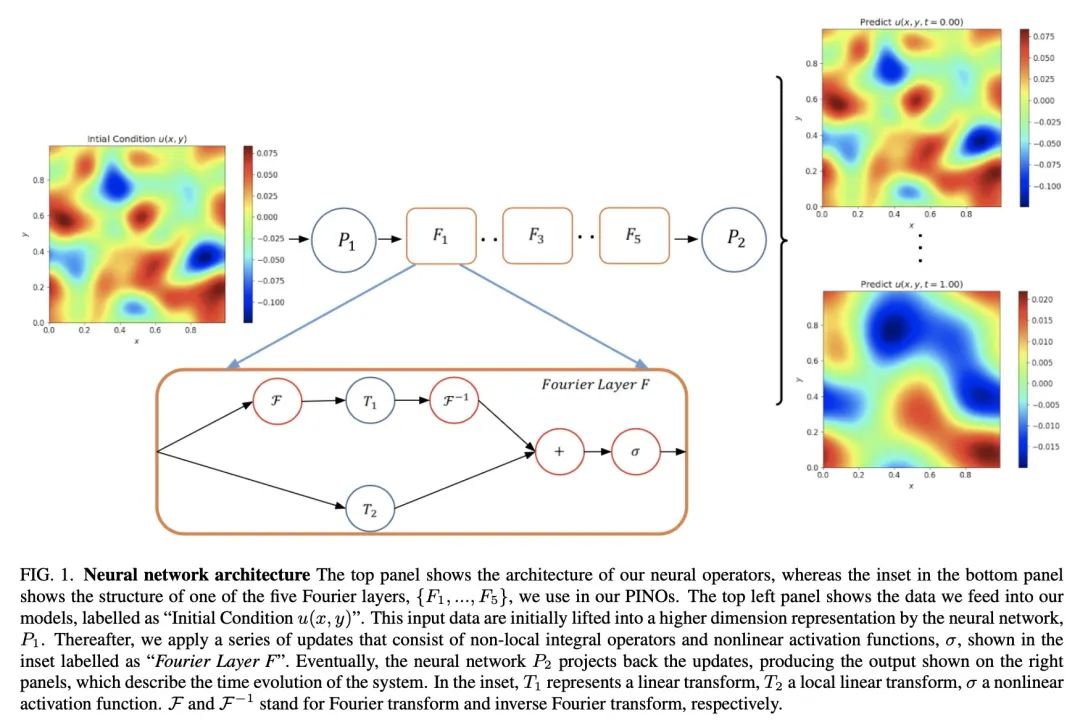
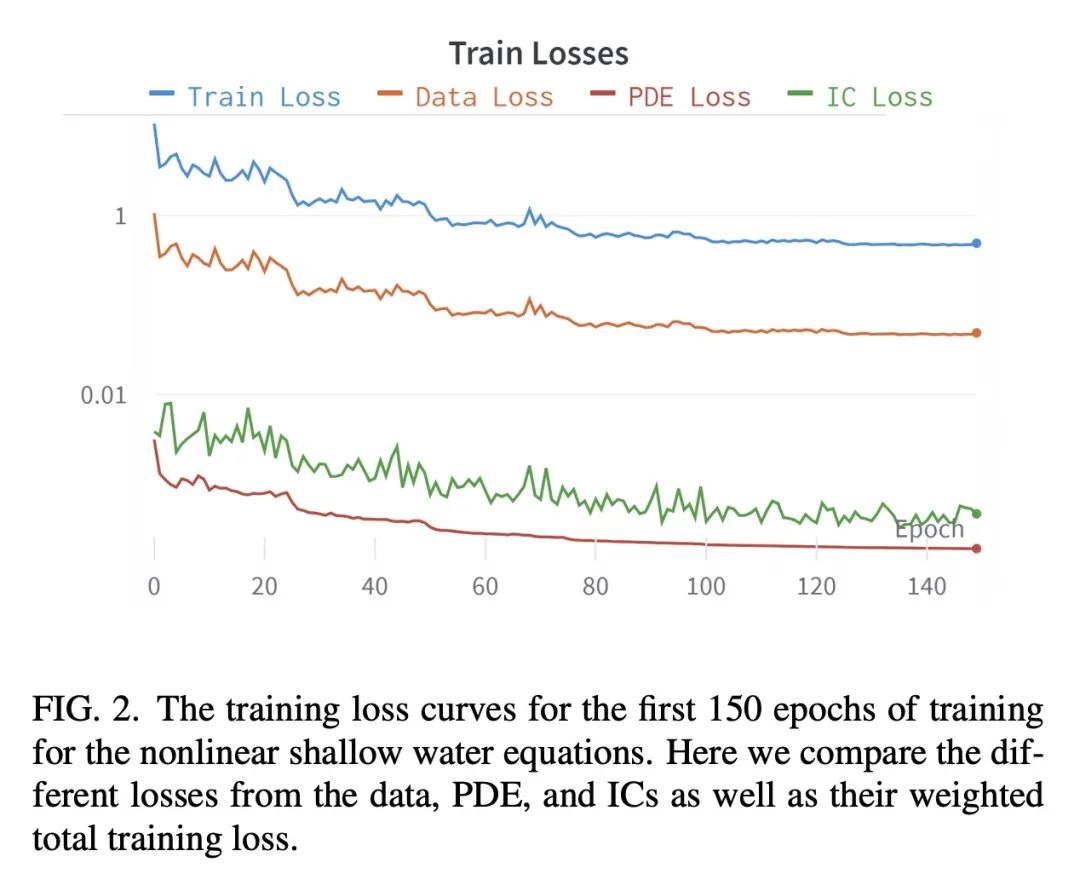
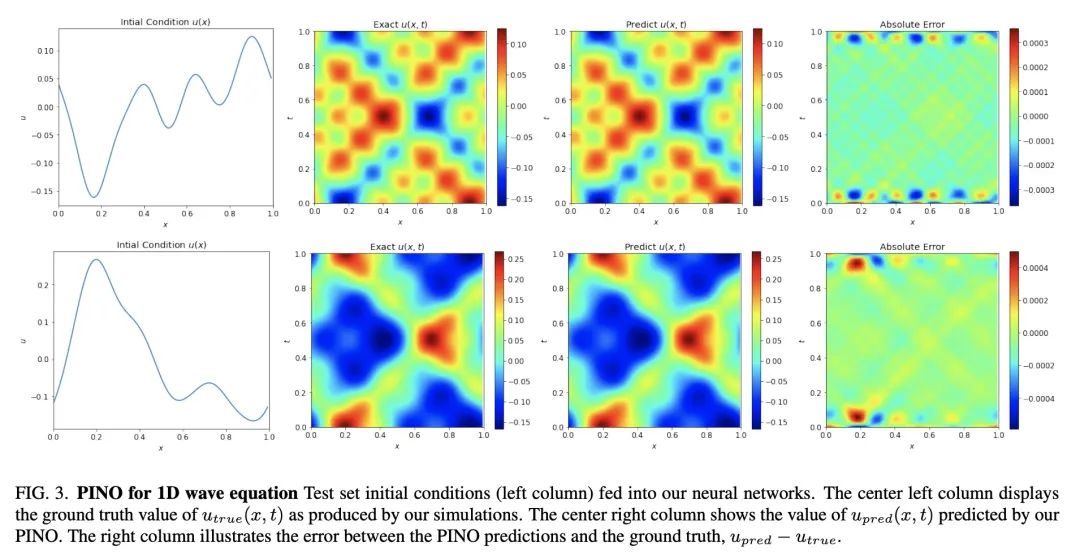
摘要：本文提出一种端到端框架来学习偏微分方程，该框架将初始数据生成、边界条件的选择以及使用物理嵌入神经算子结合在一起来求解物理研究和建模中普遍存在的偏微分方程现象。 首先证明该方法再现了文献中其他地方发表的其他神经算子的准确性和性能，以学习一维波动方程和一维伯格斯方程。 应用所提出的物理嵌入神经算子来学习新型方程，包括标量、无粘性和矢量类型的2D Burgers方程，表明该方法也适用于学习二维线性和非线性浅水方程的物理学，其中涉及三个耦合偏微分方程。

We present an end-to-end framework to learn partial differential equations that brings together initial data production, selection of boundary conditions, and the use of physics-informed neural operators to solve partial differential equations that are ubiquitous in the study and modeling of physics phenomena. We first demonstrate that our methods reproduce the accuracy and performance of other neural operators published elsewhere in the literature to learn the 1D wave equation and the 1D Burgers equation. Thereafter, we apply our physics-informed neural operators to learn new types of equations, including the 2D Burgers equation in the scalar, inviscid and vector types. Finally, we show that our approach is also applicable to learn the physics of the 2D linear and nonlinear shallow water equations, which involve three coupled partial differential equations. We release our artificial intelligence surrogates and scientific software to produce initial data and boundary conditions to study a broad range of physically motivated scenarios. We provide the source code, an interactive website to visualize the predictions of our physics informed neural operators, and a tutorial for their use at the Data and Learning Hub for Science.

论文链接：https://arxiv.org/abs/2203.12634

内容中包含的图片若涉及版权问题，请及时与我们联系删除