基于观测数据的因果发现及因果性学习

因果关系一直是人类认识世界的基本方式和现代科学的基石，可以帮助我们理解很多复杂的现实场景。与相关关系对比，因果关系严格区分了“原因”变量和“结果”变量，在揭示事物发生机制、指导干预行为等方面有相关关系不能替代的重要作用。

 

1. 如何发现因果结构

认识事物间的因果关系，最直接的方法是做随机实验，但在现实生活中，随机实验有时不具备可操作性，我们越来越希望能够从观测数据中得到因果关系，这其中最基本的核心点是需要找到有助于我们发现因果关系的额外信息，建立起因果结构和观测的统计数据之间的桥梁，下面介绍三种常用的方法：

 

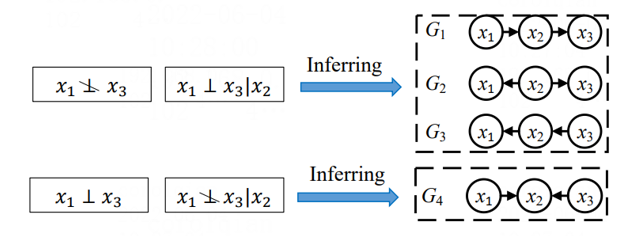
1）基于约束的方法：主要是PC（Peter-Clark）算法和IC（Inductive Causality）算法，核心原理是基于独立性和条件独立性判断变量之间的独立性，获得因果图，并利用V-结构和定向规则对变量间的无向边进行定向。这种方法的缺点是无法区分马尔可夫等价类结构。

 

图1：基于约束的因果关系发现方法

 

2）基于因果函数模型的方法：主要是加性噪声模型（ANM）和后非线性模型（PNL），核心原理是假设结果Y和原因X具有函数关系，如果X对Y做正向回归，噪声项与X独立，Y对X做反向回归，噪声项与Y不独立，则推断X是Y的原因。

 

图2：基于因果函数模型的因果关系发现方法

对于离散的类别型数据，由于无法直接定义加法操作和回归函数操作，为了发现不对称性，可以通过在 “X -> Y’ -> Y”前后两个过程中建立似然度函数来保证模型的可识别性，找到X和Y之间的因果关系。

 

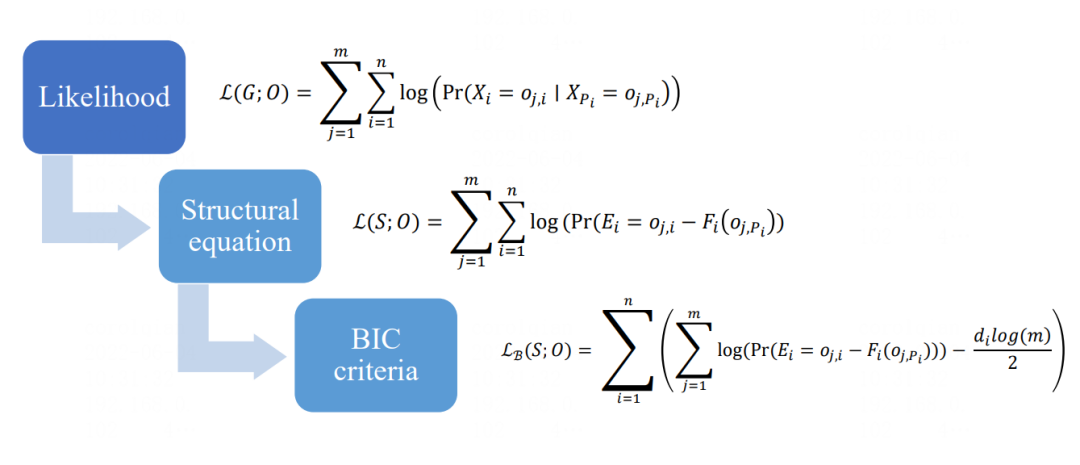
3）混合型方法：由于基于约束的方法，无法识别马尔可夫等价类的问题，而基于因果函数模型的方法，只能判断一个变量对结果变量的影响，无法解决实际生活中多变量的问题，两类方法在现实中均存在一定的不适用性。为了解决这一问题，引入混合型方法，核心原理是将似然度框架嵌入因果函数模型，发现数据间的因果结构。

 

图3：混合型因果关系发现方法

 

2. 隐变量场景下，如何发现因果结构

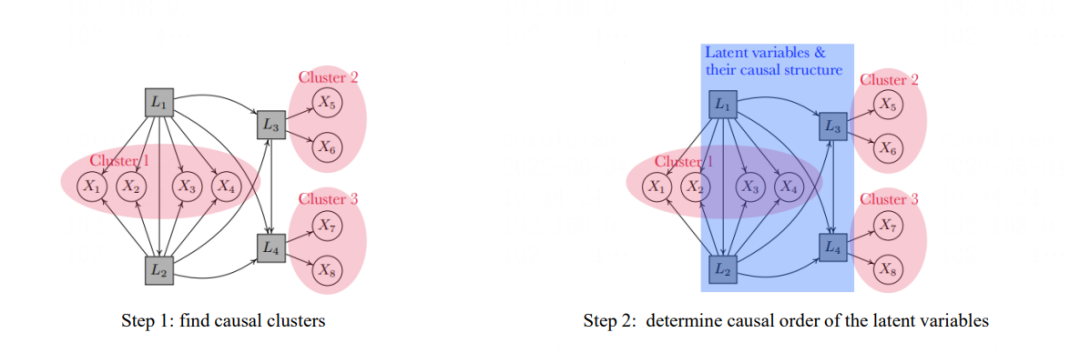
现实场景中，经常有许多存在隐变量的情况，如果数据是线性非高斯的，可将独立噪声条件（IN）扩展到广义独立噪声条件（GIN），通过找到隐变量的代理变量做回归，恢复数据的因果结构。具体步骤：

1）找到共享同样的隐变量父节点的观察变量cluster；

2）根据隐变量与观察变量cluster的关系，找到不用隐变量之间的关系。

图4：隐变量场景下因果关系发现方法

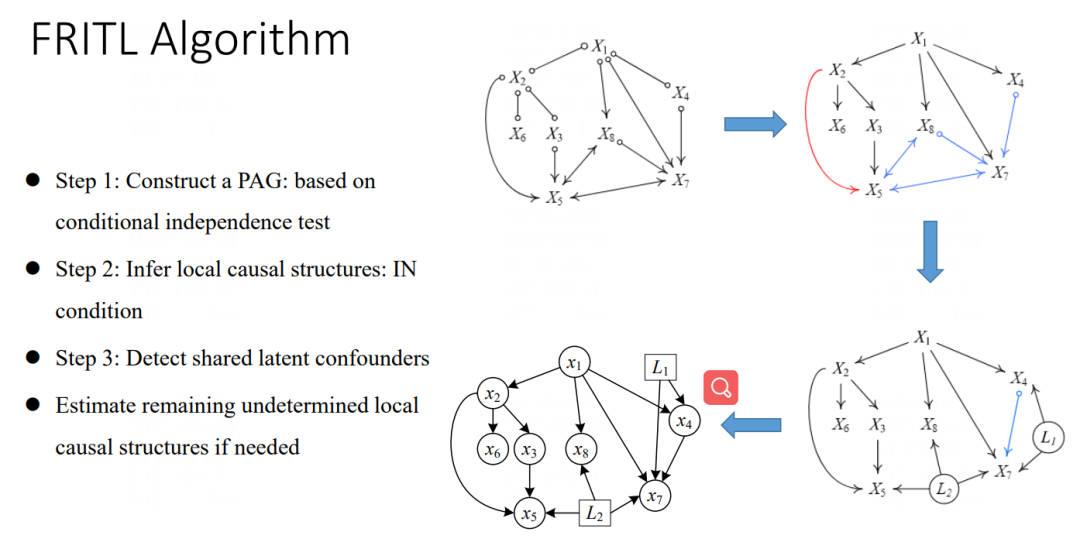
但这种方法的局限性在于其认为观测变量之间没有边，无法推断变量之间完整的因果关系，在此基础上可以利用面向不完全观察数据的因果结构学习算法（FRITL算法）做进一步的优化，具体步骤：

1）基于独立性条件利用FCI方法构建祖先图（PAG）；

2）利用独立噪声条件（IN）推断每个祖先图（PAG）局部的因果方向；

3）局部的因果方向无法判别时，引入隐变量，利用三分体约束，检测并合并同一个隐变量，估计未确定的局部因果结构。

图5：隐变量场景下利用FRITL算法的因果关系发现方法

 

3. 因果性学习在人工智能中的应用

正如图灵奖得奖者Pearl Judea提出的 “因果关系之梯” 中特别指出，我们当前的机器学习只处于第一层，只是“弱人工智能”，要实现“强人工智能”还需要干预和反事实推理。因果推断对于克服现有人工智能在抽象、推理、可解释性等方面的不足具有重要意义，比如

 

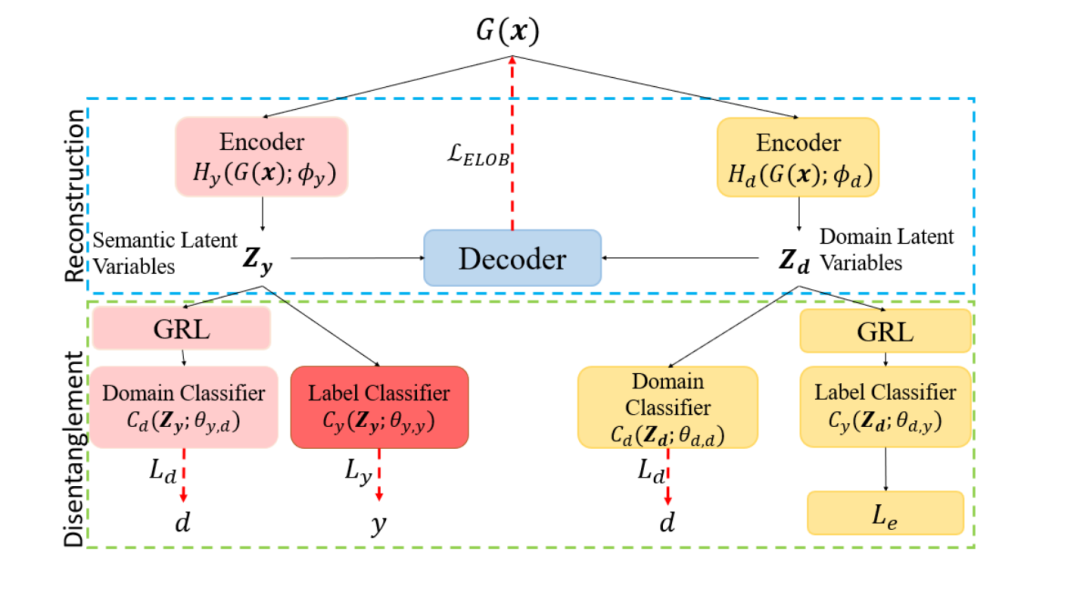
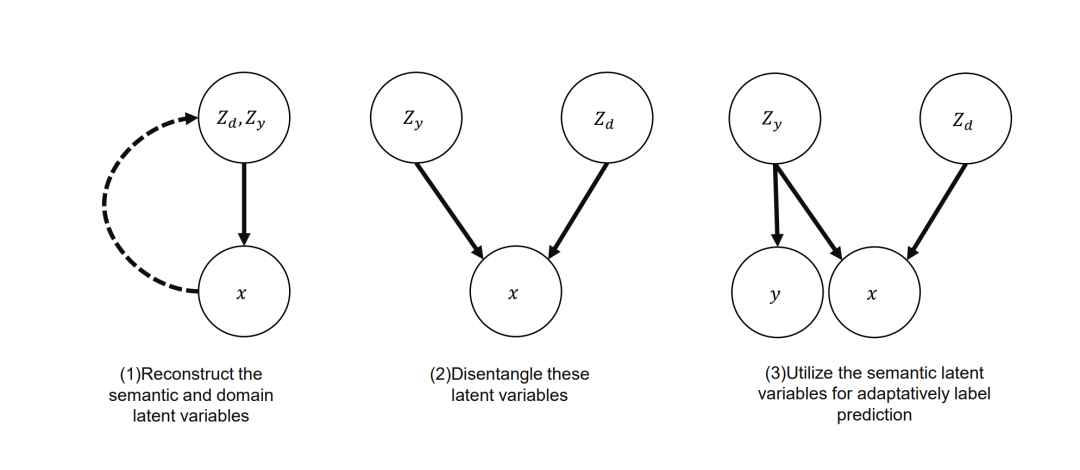
（1）在领域迁移中，可以基于因果机制抽象出语义信息实现领域自适应（domain adaptation），解决方案是利用变分自编码器（VAE）框架，在隐空间（latent space）中，从x学到label y和domain的隐变量，再基于监督信号，将label相关的信息和domain相关的信息解耦，把语义的label信息单独抽离出来进行判别，这种方法在剪切图、艺术图、产品图上都取得了较好的实验效果。

 

图6：领域迁移中的解耦方法

图7：领域迁移中的解耦步骤

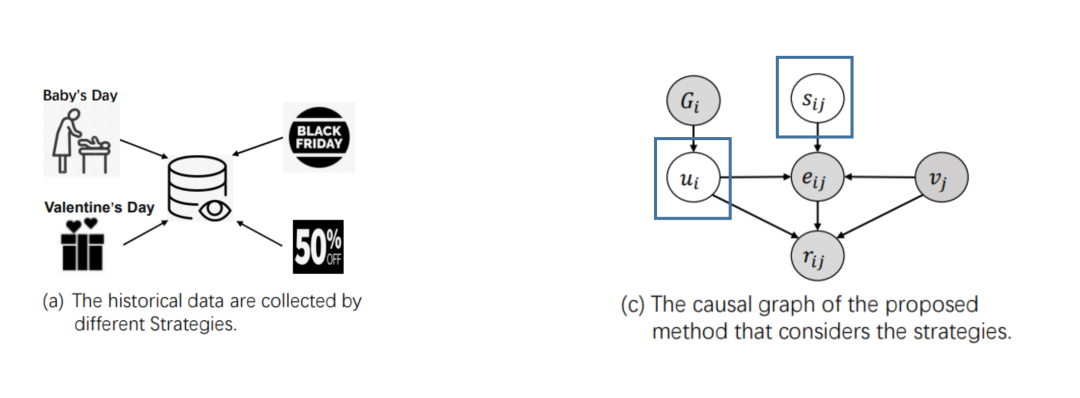
（2）在推荐系统中，我们可以利用因果图解决自选择偏差的问题。假设历史数据是多种营销策略的混合体（s_ij），且我们可以通过社交网络（G_i）来推断u_i的信息，通过建立因果图，可以看到s_ij节点附近形成两个v结构，通过e_ij、v_j、u_i等变量信息我们就可以推断s_ij的信息，从而帮助我们推断历史上采取了哪些不同的营销策略，进而辅助提升推荐的效果。

图8：推荐系统解决自选择偏差的方法