
论文链接:
https://openreview.net/pdf?id=7WGNT3MHyBm
代码链接:
https://github.com/chr26195/GKD
01. 简介
现目前有很多工作开始关注图数据的泛化和迁移问题,然而很少有研究在泛化相关的问题上考虑拓扑信息。在这个工作中,我们提出了一种全新的基于拓扑的知识迁移范式,即几何知识蒸馏(Geometric Knowledge Distillation),它可以实现两个定义在不一致的图拓扑上的图神经网络(GNN)之间实现知识迁移。为了实现这个目标,我们首先回顾了从热力学的角度联系热传导方程(Heat Equation)和图神经网络特征传递的过程。
在这一理论框架下,我们提出了神经热核函数 (Neural Heat Kernel, NHK) 将图神经网络背后的流形的几何特性编码成一系列层间的矩阵表示。几何知识蒸馏通过挖掘和对齐教师和学生GNN模型的神经热核,实现将图拓扑信息压缩到模型本身并实现不同GNN之间的知识迁移。我们继而设计了非参数化和参数化的两类模型变种,并在多个图数据知识迁移任务上,如不同图拓扑间的知识迁移、不同大小GNN间的知识蒸馏、通过自蒸馏(Self-Distillation)实现性能提升等,验证了它们的有效性。
02. 从热传导方程到图神经网络
首先,我们简单介绍技术背景。在物理学中,黎曼流形上的热传导过程可以用如下的偏微分方程描述。其中,c表示导热系数, x(u,t): M×[0,∞)→Rd 表示定义在流形上的一个函数,用来表示某个点和时间上的某种信号,例如温度或者其他特征。 表示Laplace-Beltrami operator,可以进一步写成 ∇∗ (Divergence operator)和 ∇ (Gradient operator)的复合函数(即 )。
上述偏微分方程的含义可以直观理解为:某一点的信号/温度在无穷小时间间隔内的变化等同于该点信号/温度与其周围区域平均信号/温度的差异。近期,一系列工作 [1-5] 揭示了 GNN 的特征传播过程和底层黎曼流形的热扩散的联系。如下图所示,图拓扑结构(由节点和边构成)可以被看作空间离散化(Spatial discretization)后的黎曼流形,而进一步将热传导方程以数值求解的方法(例如用Euler method求解)进行时间离散化(Temporal discretization)就可以产生一层的 GNN 架构。换句话说,在黎曼流形上一定时间间隔的热传导可以看做一层 GNN 做特征传递(如下图所示)。
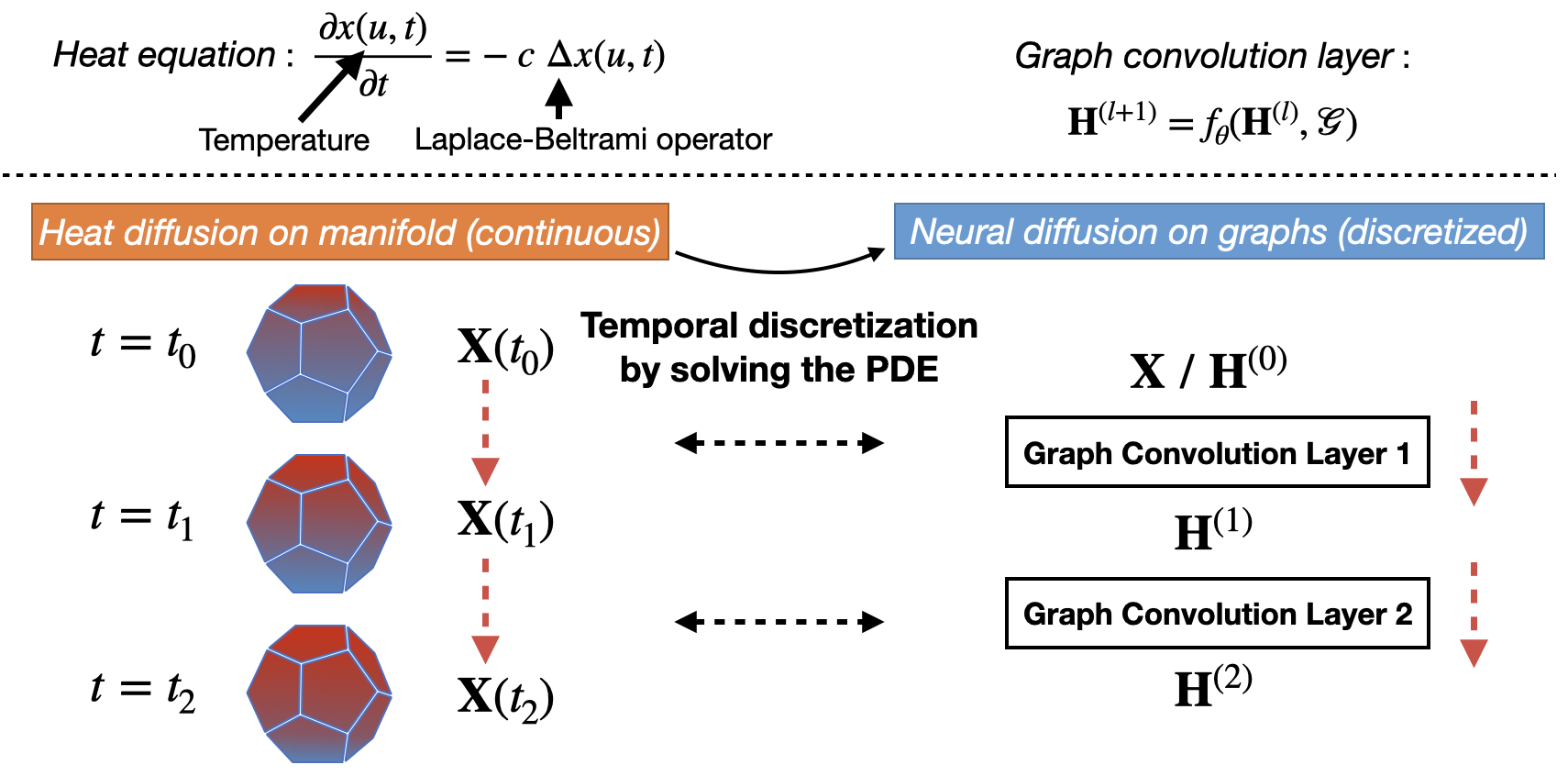
另外,不同的 Δ定义或者不同的数值求解方法可以产生不同的 GNN 模型结构:例如,将 定义为计算相邻节点特征的差值,∇∗ 定义为对特征差值的求和,并用forward Euler method求解热传导方程,就可以得到一层GCN形式 [6] 的特征传递层。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢