悲观和推广的经验伯恩斯坦不等式

来自今天的爱可可AI前沿推介

[LG] Policy learning "without'' overlap: Pessimism and generalized empirical Bernstein's inequality

Y Jin, Z Ren, Z Yang, Z Wang
[Stanford University & University of Chicago & Yale University & Northwestern University]

“没有重叠”的策略学习：悲观和推广的经验伯恩斯坦不等式

要点:

1. 算法优化策略值的较低置信界(LCB)，而不假定任何统一的重叠条件；
2. 建立了一个数据相关的最大次优上界，只取决于最优策略的重叠程度和优化策略类的复杂度；
3. 开发了一种新的自标准化类型浓度不等式，用于反比例加权估计，将众所周知的经验伯恩斯坦不等式推广到无界和非独立同分布的数据。

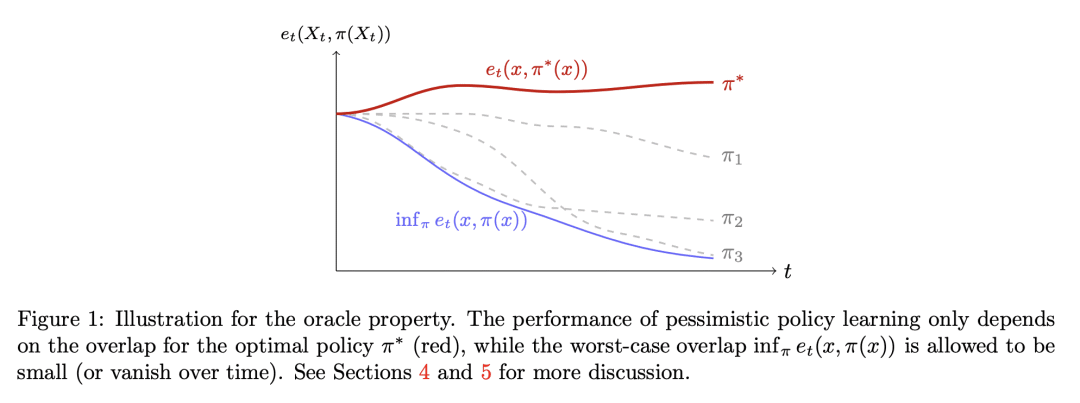
摘要：本文研究离线策略学习，旨在利用先验收集的观察结果(来自固定或适应性演化的行为策略)来学习最佳的个性化决策规则，为特定种群实现最佳的总体结果。现有的策略学习方法依赖于一个统一的重叠假设，即探索所有单个特征的所有操作的倾向在离线数据集中是有下界的；换句话说，现有方法的性能取决于离线数据集中的最坏情况倾向。由于无法控制数据收集过程，因此在许多情况下，这种假设可能是不现实的，特别是当行为策略随着时间的推移随着某些行动倾向的降低而演化时。本文提出一种优化策略值的较低置信界(LCB)以取代点估计的新算法。LCB用收集离线数据的行为策略知识构建。在不假设任何统一重叠条件的情况下，为算法的次优性建立了一个与数据相关的上界，这仅取决于 (i) 最优策略的重叠，以及 (ii) 优化策略类的复杂性。这意味着，对于适应性收集的数据，只要最佳行动的倾向随着时间的推移而降低，而次优行动的倾向被允许任意快速减少，就能确保高效的策略学习。在本文提供的理论分析中，为逆倾向加权估计器开发了一种新的自归一化类型浓度不等式，将众所周知的经验伯恩斯坦不等式推广到无界和非独立同分布的数据。

This paper studies offline policy learning, which aims at utilizing observations collected a priori (from either fixed or adaptively evolving behavior policies) to learn an optimal individualized decision rule that achieves the best overall outcomes for a given population. Existing policy learning methods rely on a uniform overlap assumption, i.e., the propensities of exploring all actions for all individual characteristics are lower bounded in the offline dataset; put differently, the performance of the existing methods depends on the worst-case propensity in the offline dataset. As one has no control over the data collection process, this assumption can be unrealistic in many situations, especially when the behavior policies are allowed to evolve over time with diminishing propensities for certain actions. In this paper, we propose a new algorithm that optimizes lower confidence bounds (LCBs) -- instead of point estimates -- of the policy values. The LCBs are constructed using knowledge of the behavior policies for collecting the offline data. Without assuming any uniform overlap condition, we establish a data-dependent upper bound for the suboptimality of our algorithm, which only depends on (i) the overlap for the optimal policy, and (ii) the complexity of the policy class we optimize over. As an implication, for adaptively collected data, we ensure efficient policy learning as long as the propensities for optimal actions are lower bounded over time, while those for suboptimal ones are allowed to diminish arbitrarily fast. In our theoretical analysis, we develop a new self-normalized type concentration inequality for inverse-propensity-weighting estimators, generalizing the well-known empirical Bernstein's inequality to unbounded and non-i.i.d. data.

论文链接：https://arxiv.org/abs/2212.09900

内容中包含的图片若涉及版权问题，请及时与我们联系删除