完整题目:Is Model Ensemble Necessary? Model-based RL via a Single Model with Lipschitz Regularized Value Function
问题:previous works only directly apply probabilistic dynamics model ensemble in their methods without an in-depth exploration of why this structure works. There still lacks enough theoretical evidence to explain the superiority of probabilistic neural network ensemble. In addition, extra computation time and resources are needed to train an ensemble of neural networks.主要是为什么MBPO这样的probabilistic dynamics model ensemble好?以及时间资源消耗。
之前的工作如何解决:
-
model free中有人尝试平滑value function: -
加噪声平滑 -
鲁棒性an adversarially robust policy. -
model based有人吧平滑性和model联系起来,但没有和value function
为什么比之前的好:
-
反正他是第一个把平滑value平滑结合进model based场景,提高了MBPO的效果。
主要逻辑:
-
MBPO好是因为随机选一个模型的s‘在不确定的地方s’有大差异,能增加之后value更新的平滑性 -
model error似乎不能很好的代表策略性能,而Value-aware model error可以,Value-aware model error实际上是给定一个V函数,dynamic导出的target和真实模型导出的target的差距: -
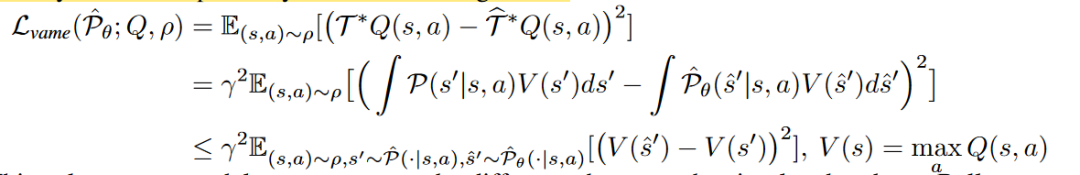
-
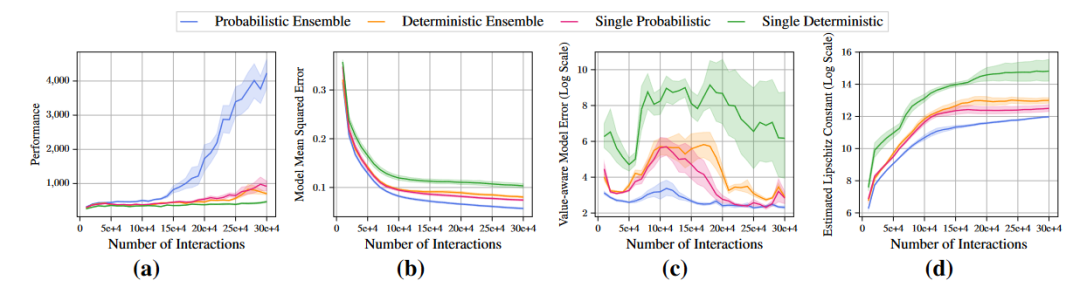
实验表明平滑性越好,Value-aware model error越好,效果越好,但model预测s‘的误差都差不多: -
-
结论是:By augmenting the transition with a diverse set of noise and then training the value functions with such augmented samples, it implicitly regularizes the local Lipschitz condition of the value network over the local region around the state where the model prediction is uncertain.在ood的sa上由于模型不确定,估出的V会很平滑。 -
所以想办法控制ood sa的价值函数平滑性(认为当前策略的sa都是ood的),和回归误差做出平衡。
方法:
-
直接对神经网络做出平滑性控制:In particular, during each forward pass, we approximate the spectral norm of the weight matrix ∥W ∥2 with one step of power iteration. Then, we perform a projection step so that its spectral norm will be clipped to β if bigger than β, and unchanged otherwise.具有全局性,平滑太强,效果不好。 -
只在数据点局部平滑: -
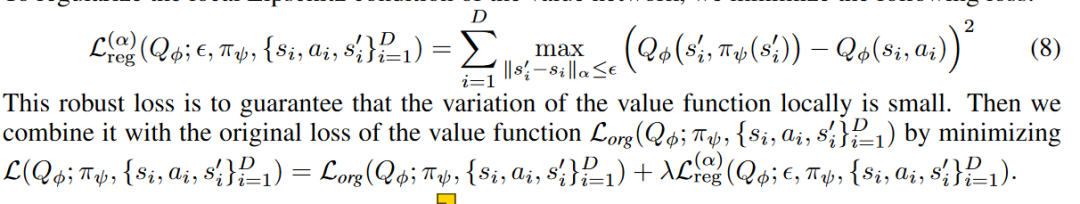
实验:
-
平滑性和Q网络回归误差(贝尔曼误差)与效果的关系:直觉上,target网络越平滑,回归误差越大,在s’预测误差相同时肯定target的误差越小。 -
加上value鲁棒性平滑后效果和其他baseline比不错:
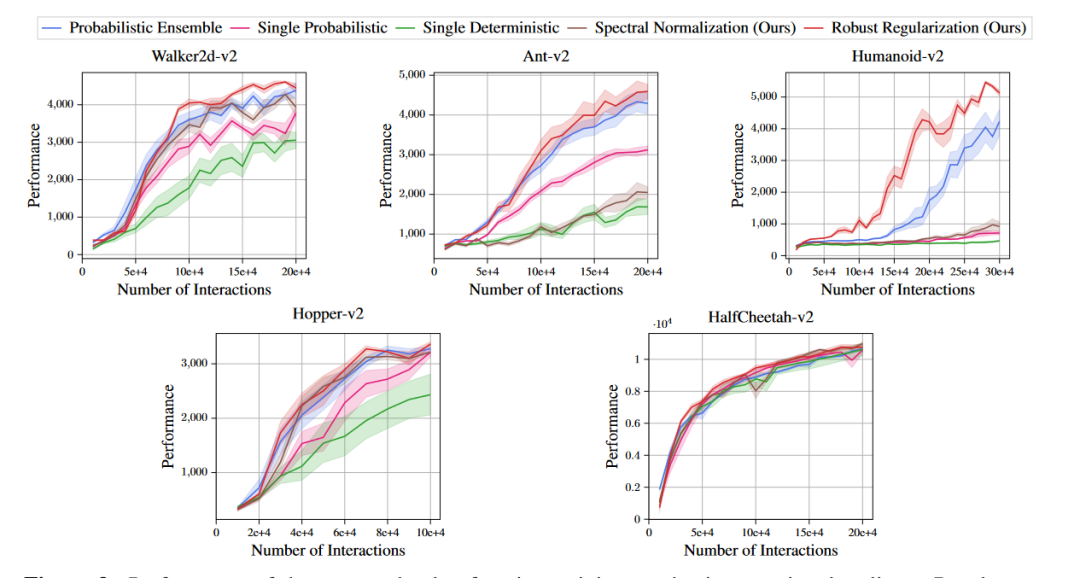
-
随机噪声比对抗性选择噪声差,但也可以平滑,降低一点value-aware-model-error,提升一点performance。 -
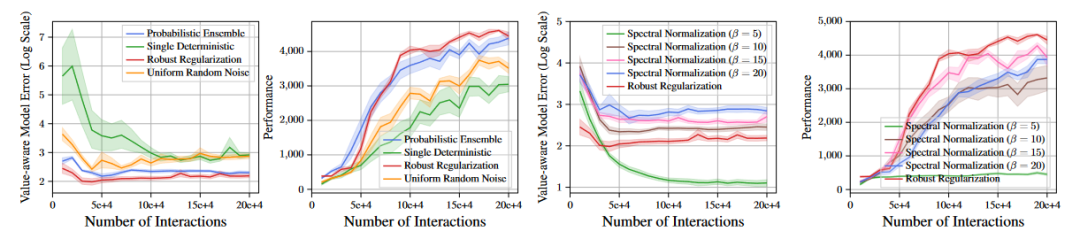
-
在model free上的value加平滑也有点提升 -
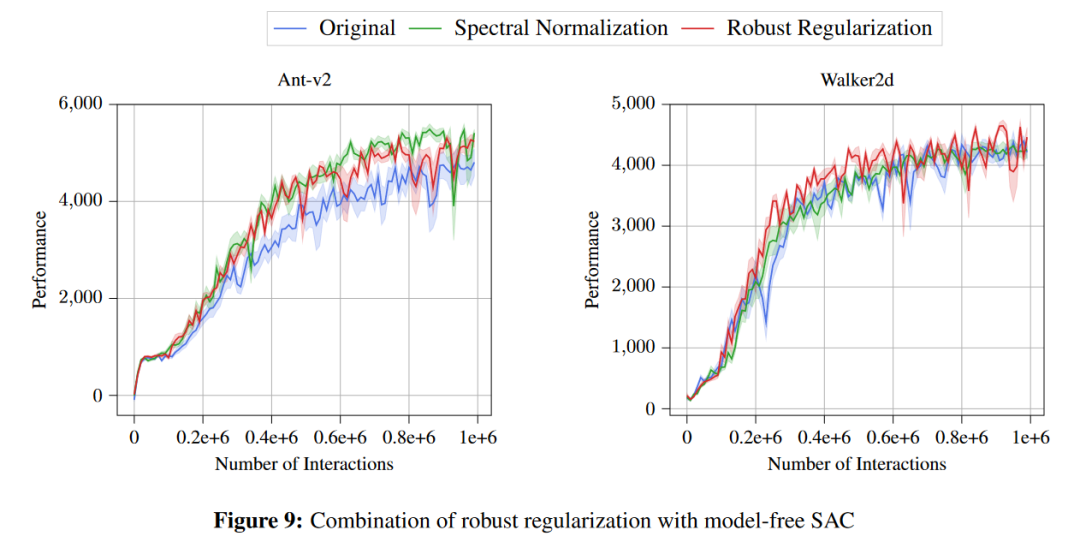
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢