【隐私计算笔谈】MPC系列专题（八）：OT协议（一）

通用的半诚实公钥OT协议

 

之前已经介绍过Naor-Pinkas不经意传输协议，Naor-Pinkas不经意传输协议基于离散对数困难问题，这次介绍一个通用的基于公钥的半诚实安全的不经意传输协议和Beaver的非黑盒构造。

 

有一个发送方Alice和一个接收方Bob，这个协议的前提条件是能够在公钥空间里随机采样获得一个公钥。而不是先获得私钥，再通过私钥产生公钥。

 

简单的说就是能够随机生成一个和公钥格式相同的随机数。Alice在协议中的输入为秘密值𝑥₀,𝑥_1，Bob在协议的输入为选择比特𝑏∈{0,1} 。

 

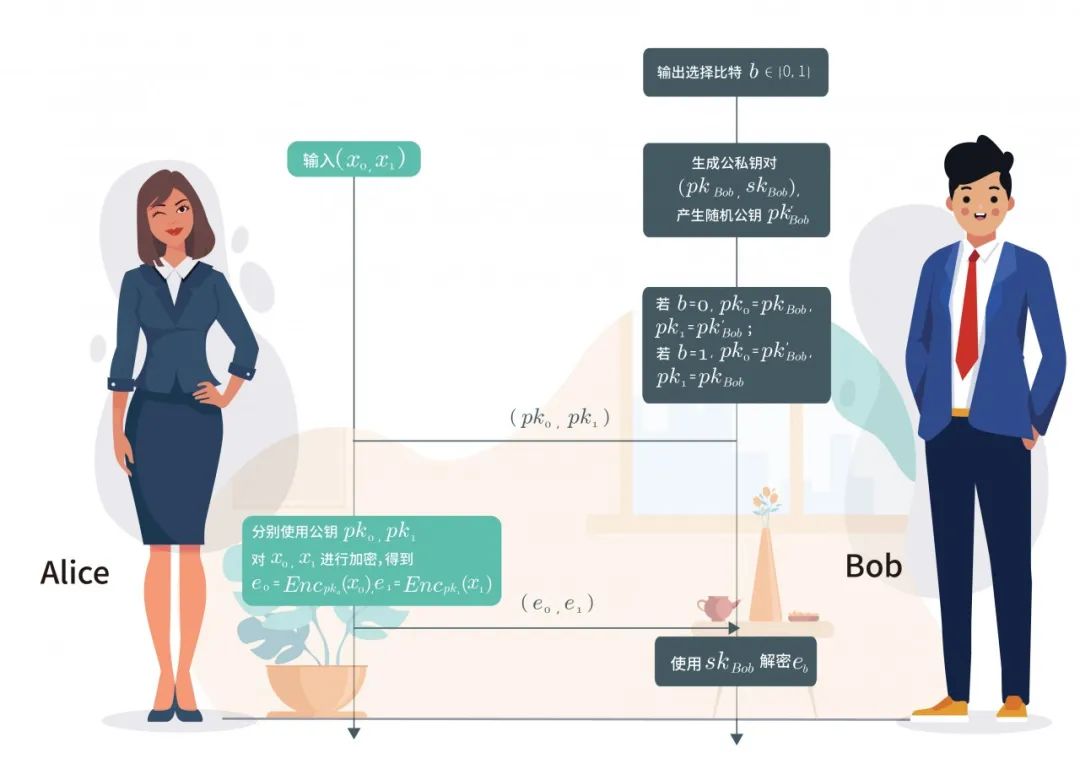
协议开始时，Bob首先生成一个公私钥对(𝑝𝑘_Bob,𝑠𝑘_Bob)，并在公钥空间里进行随机采样，再生成一个随机公钥𝑝𝑘′_Bob，Bob根据自己输入的选择比特b，如果选择比特𝑏=0，那么Bob将(𝑝𝑘_Bob, 𝑝𝑘′_Bob)发送给Alice；如果选择比特𝑏=1，那么Bob将(𝑝𝑘′_Bob, 𝑝𝑘_Bob)发送给Alice。

 

将Alice从Bob那收到的公钥记为(𝑝𝑘₀,𝑝𝑘₁)，Alice收到Bob发来的公钥对后，向Bob发送两个密文(𝑒₀,𝑒₁)，其中

 

𝑒₀=𝐸𝑛𝑐_𝑝𝑘0(𝑥₀),𝑒₁=𝐸𝑛𝑐_𝑝𝑘1(𝑥₁)

 

𝐸𝑛𝑐_y(𝑥)指用加密算法Enc和加密秘钥y加密x。

 

Bob 接收到(𝑒₀,𝑒₁)后，使用自己的私钥𝑠𝑘_Bob解密密文𝑒_𝑏。

 

 

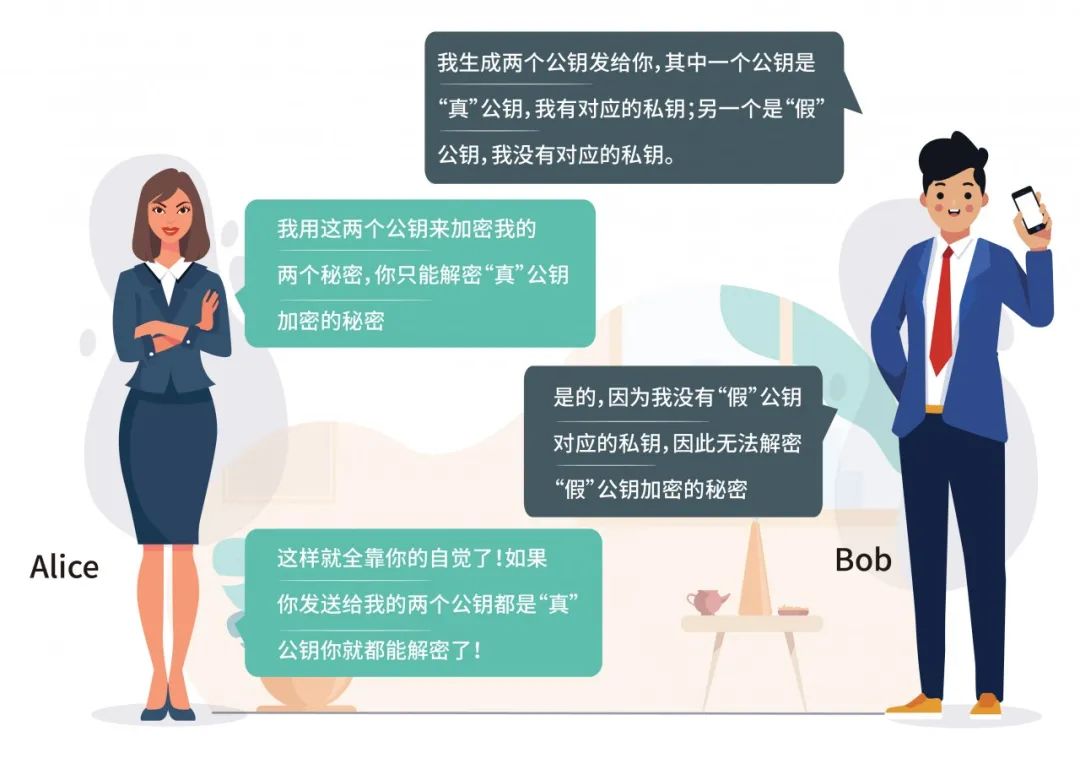
该不经意传输协议基于半诚实的，即Bob和Alice都不会违反协议，遵守协议的规定，Bob产生的公钥𝑝𝑘′_Bob是随机产生的，Bob无法得知公钥𝑝𝑘′_Bob所对应的私钥。

 

如果Bob是恶意的用户，不遵守协议规定，先产生一个私钥𝑠𝑘′_Bob后再根据𝑠𝑘′_Bob产生对应的公钥𝑝𝑘′_Bob，则Alice发送过来的(𝑒₀,𝑒₁)Bob均可解密，所以协议前提是半诚实的。

 

Bob不知道𝑝𝑘′_Bob所对应的私钥，也就只能解密(𝑒₀,𝑒₁)其中之一，无法解密Alice使用𝑝𝑘′_Bob加密的𝑥_1-b。 

 

 

Beaver的非黑盒构造

之前介绍过的多个混淆电路估值协议都需要使用到不经意传输协议，Beaver提出了一种自举姚氏混淆电路协议（bootstrapping Yao’s GC protocol），可以用少量的公钥密码学操作生成多项式数量级的不经意传输协议。 

 

假设Alice是发送方，Bob是接收方。有一个布尔电路C，该电路能够实现不经意传输函数F，函数F的输入是加密过的Bob的选择比特串以及Alice的秘密值对，输出是OT协议的执行结果。有一个伪随机函数𝐺(𝑥)，可以将𝑘比特的输入𝑥扩展到𝑚比特。

 

Bob产生𝑚比特长的选择比特串𝑏，和𝑘比特长的随机比特串𝑟，利用伪随机函数𝐺(𝑟)来将𝑟扩展到𝑚比特长，之后Bob向Alice发送𝐺(𝑟)⨁𝑏。

 

Alice收到𝐺(𝑟)⨁𝑏后，将收到的𝐺(𝑟)⨁𝑏和自己持有的秘密值对 

 

{(𝑥₁₀,𝑥₁₁),(𝑥₂₀,𝑥₂₁),…,(𝑥_m0,𝑥_m1)}

 

作为函数F的输入。之后Bob再向函数F输入𝑟，函数F会通过由Bob输入的𝑟计算出𝐺(𝑟)后对𝐺(𝑟)⨁𝑏进行解密得到𝑏，再利用选择比特串𝑏从Alice的秘密值对中进行选择，并输出选择结果。

 

 

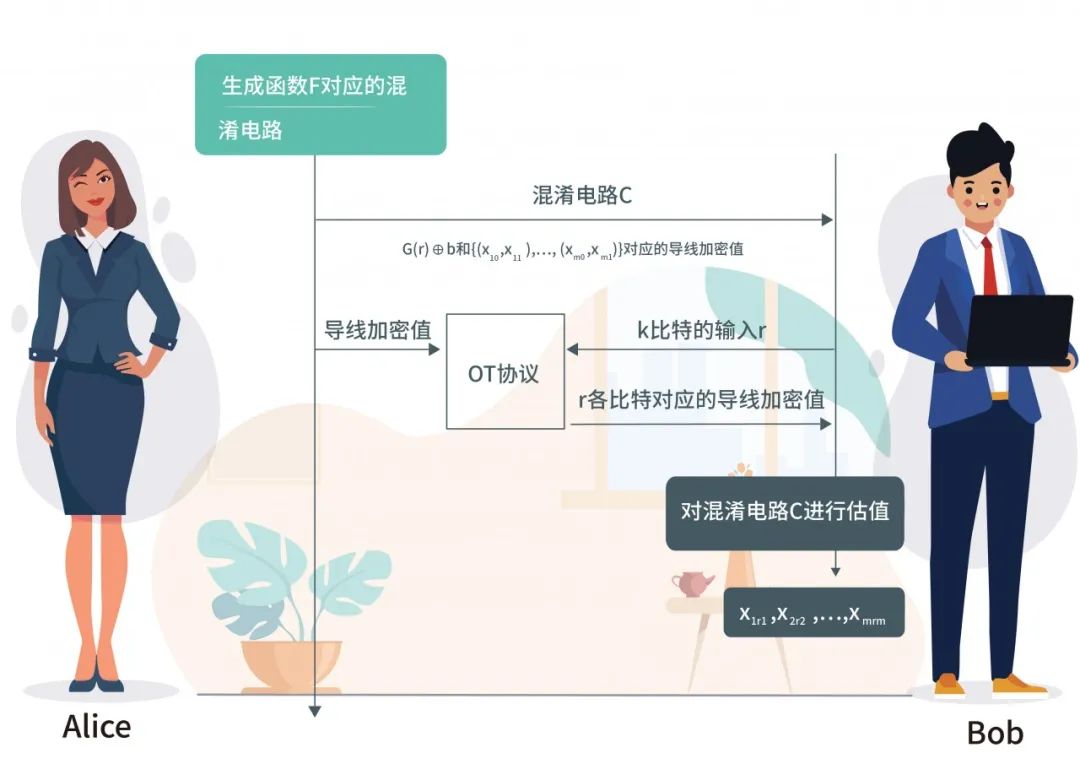
即对于函数F而言，它只需要Bob的𝑘比特的输入𝑟。函数F的实现可以通过混淆电路，在Alice由于不知道𝑟，因此无法解密出𝑏。Alice计算函数F对应的布尔电路后，对其进行混淆。

 

之后Alice将混淆电路以及𝐺(𝑟)⨁𝑏和{(𝑥₁₀,𝑥₁₁),(𝑥₂₀,𝑥₂₁),…,(𝑥_m0,𝑥_m1)}对应的导线加密值发送给 Bob，Bob则通过𝑘次OT协议获取对应的输入导线的加密值，进行电路估值。 

 

若𝐺(𝑟)⨁𝑏已经在协议开始之前发送给了Alice，那么 Bob在协议中需要输入的只有𝑘比特随机比特串𝑟，由于混淆电路的输入比特数量和需要执行的OT次数相关联，Alice预先生成混淆电路后发送给Bob，Bob通过𝑘次OT获取输入𝑟的各个比特对应的混淆秘钥，进行电路估值。

 

若不使用这种结构直接进行OT协议，由于选择比特串𝑏是𝑚比特长，因此需要𝑚个OT协议。通过这种构造成功将𝑚个OT协议降为了𝑘个OT协议。

​

内容中包含的图片若涉及版权问题，请及时与我们联系删除