ZARTS：非梯度更鲁棒的神经网络架构搜索

截屏20221226 11.02.39.png

论文链接：https://openreview.net/pdf?id=QzFJmwwBMd
代码链接：https://github.com/vicFigure/ZARTS

导读

可微分架构搜索(DARTS)是一种高效的模型架构搜索(NAS)算法。它定义了可训练的架构参数来表示各种候选运算和网络连接的重要性，并提出一阶/二阶近似策略来估计架构参数的梯度。然而，我们通过实验结果表明，这种一阶/二阶近似策略会影响损失函数，使优化目标产生偏差，进而影响对架构参数梯度的估计。本工作尝试使用零阶优化方法，无需利用上述近似策略估计梯度，提出了一种称为 ZARTS的模型架构搜索方法。

本文具体介绍了三种有代表性的零阶优化方法：Random Search(RS)、Maximum-likelihood Guided Parameter Search(MGS)和GradientLess Descent(GLD)。我们探索了零阶优化方法（ZARTS）与梯度下降算法（DARTS）之间的联系，并证明在一阶/二阶的近似的条件下，ZARTS可以退化为DARTS方法。本文通过大量实验验证了零阶优化搜索方法的鲁棒性和有效性。在DARTS的标准搜索空间下，ZARTS搜索到的架构在 CIFAR-10 上达到了 97.54% 的准确率，在 ImageNet 上达到了 75.7% 的 top-1 准确率。最后，我们通过实验证明当ZARTS与其他策略进行结合，可以进一步提升其搜索性能和搜索速度。

本工作的贡献：

我们首次利用零阶优化方法求解模型架构搜索的双层优化问题。本文通过实验说明DARTS方法使用的一阶/二阶近似策略会影响损失函数，进而使优化目标产生偏差，并通过实验说明零阶优化比梯度下降会有更好的收敛效果。
我们探索了ZARTS与DARTS之间的联系，表明在一阶/二阶的近似的条件下，ZARTS可以退化为DARTS方法。
我们通过大量实验验证了ZARTS的性能和鲁棒性。在四个数据集和五个搜索空间上，ZARTS 可以稳定地搜索到有效的架构。在 ImageNet 上，ZARTS搜索到的模型可以实现75.7%的准确率。此外，ZARTS 可以通过与其他DARTS 变体方法相结合进一步提升性能，在0.5 GPU-day的搜索耗时下，实现在 CIFAR-10 上 97.81%的准确率。

简介

DARTS根据搜索空间构造一个超网络，包含了所有可能的候选运算和连接关系，并定义可训练的架构参数 $来表示各种候选运算和网络连接的重要性，其优化目标为：$

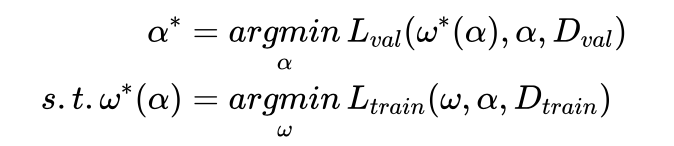
截屏20221226 11.07.30.png

式中 $ D_{val} $ $, $ D_{train} $ 分别表示验证集和训练集。为了利用梯度下降的方式来更新架构参数，DARTS根据链式法则推出 $ ∇_αL_{val}(ω^∗(α),α)=∇_{ω^∗}L_{val}(ω^∗,α)⋅∇_αω^∗(α)+∇_αL_{val}(ω^∗,α) $. 然而 $ ω^∗(α) $ 通常需要多次梯度下降更新，因此很难直接求得其对的导数，因此DARTS提出一阶和二阶近似方法。$

二阶近似： 由于网络参数w也是利用梯度下降来更新，即：$ ω←ω−ξ∇_ωL_{train}(ω,α) $ $,则二阶近似方法使用的一步更新来近似 $ ω^∗(α) $，即 $ ω^∗(α)≈ω−ξ∇_ωL_{train} (ω,α)=ω′ $ ，于是，通过链式法则可以得到：$

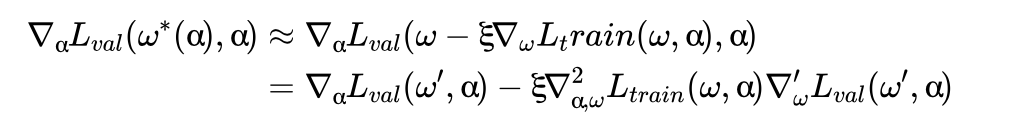
截屏20221226 11.12.04.png

式中 $ ∇_{α,ω}^2L_{train} (ω,α) $ $可以通过差分的方法进行估计，细节请参考DARTS和ZARTS的论文。$

一阶近似： 由于二阶近似的计算量很大，因此DARTS提出直接用 $来近似 $ ω^∗(α) $，即假设 $ ω^∗(α) $ 与无，则 $ ∇_αw^∗(α)=0 $ ，因此$

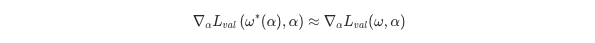
相比于二阶近似，一阶近似公式相当简洁，因此计算速度也明显快于二阶近似。

DARTS为了简便导数的计算，利用一阶/二阶近似估计最优参数 $ ω^∗(α) $ $。然而这种估计是存在很大偏差的，因为最优参数通常需要经过多次梯度下降训练才可以获得。为了验证一阶/二阶近似估计对损失函数的影响，我们绘制了在一阶/二阶近似，以及更准确的 $ ω^∗(α) $下，损失函数的分布情况。是向量，因此为了可视化，我们随机选取两个正交的方向对进行扰动，每个方向上的扰动范围为[-1,1]，以0.02为步长采样样本点，然后根据不同的近似方法获得 $ ω^∗(α) $ ，进而计算 $ L_{val}(ω^∗(α),α) $ ，绘制得到损失函数的等高线图如下所示：$

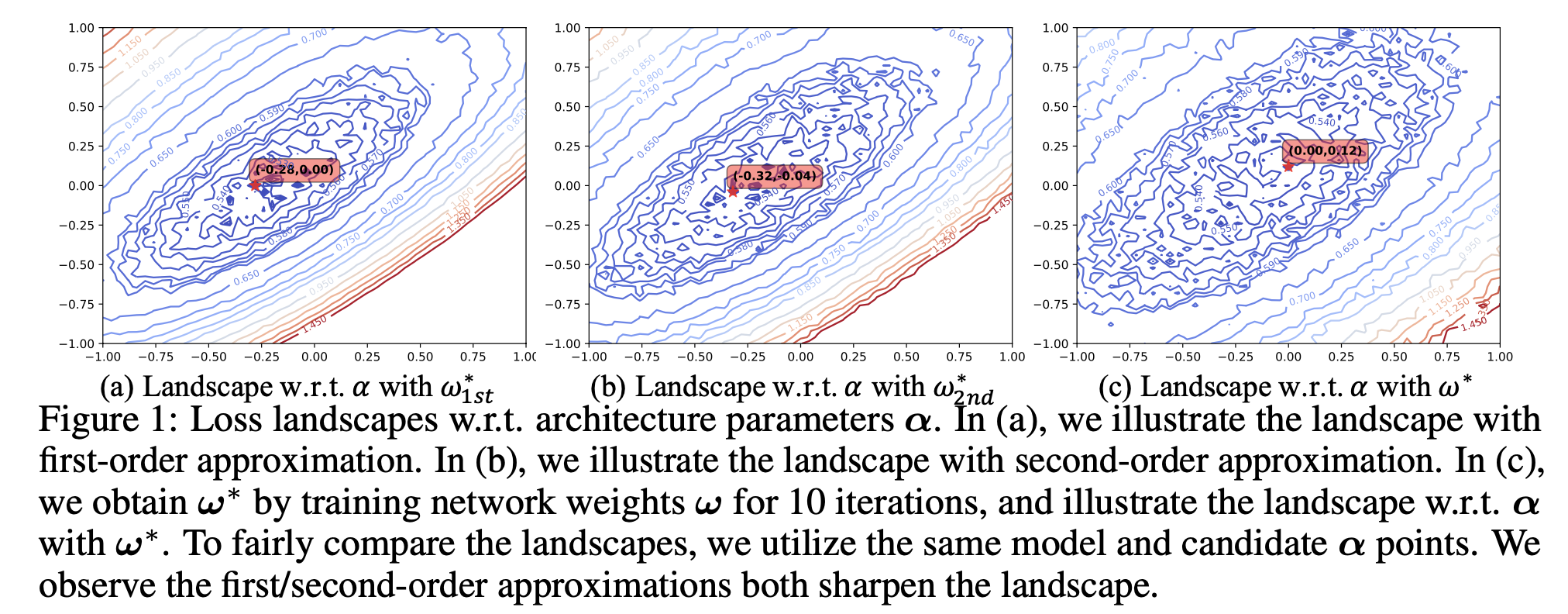
图中红色五角星标注了不同损失函数中最优点（损失函数最小）的位置，我们发现，一阶/二阶近似下（图a/图b），损失函数的分布情况明显更为陡峭（等高线更为密集），且最优点的位置也与更准确的 $ ω^∗(α) $ $（图c）下不同。通过上图，我们观察到一阶/二阶近似估计会严重影响模型架构搜索的双阶段优化目标。因此，本工作舍弃了一阶/二阶近似以获得更准确的 $ ω^∗(α) $，并提出使用零阶优化的方法取代梯度下降优化方法。$

$方法$

下述算法流程概述了ZARTS框架的通用形式。具体地，我们采用三种代表性零阶优化方法：Random Search (RS)[1], Maximum-likelihood Guided Parameter Search(MGS)[2] 和GradientLess Descent(GLD)[3]。

下面我们将详细介绍三种不同零阶优化方法的使用，为了简便书写，我们以 $ L(α)=L_{val}(ω^∗(α),α) $ $表示搜索目标。且，其中表示对的更新量。$

1 Random Search (RS):

零阶优化方法通常通过函数评值来估计对参数的更新量。单点梯度估计是最流行的算法之一[1]:

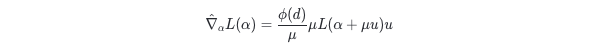
其中 $为采样到的更新方向，是平滑参数，是与参数维数相关的因子。具体地，当为标准多元正态分布时，；当为单位球体上的多元均匀分布时，。$

多点梯度估计是对单点梯度估计的拓展，可以降低其对梯度估计的方差，本工作采用多点梯度估计的方式：

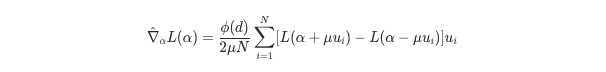
式中 $为采样点的个数，i 为第次采样下的更新方向。则对架构参数的迭代公式为：$ α←α−ξ∇_αL(α) $$

2 Maximum-likelihood Guided Parameter Search(MGS):

MGS[2]假设对参数的更新量满足如下与损失函数相关的分布：

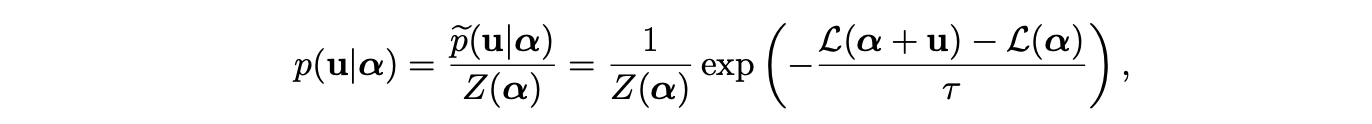
其中 $是未经归一化的概率密度，为归一化系数，为系数控制分布的方差。直观上，使损失函数降低的更新量对应更大的概率。因此MGS提出利用上述分布下的均值作为更新量，即：$

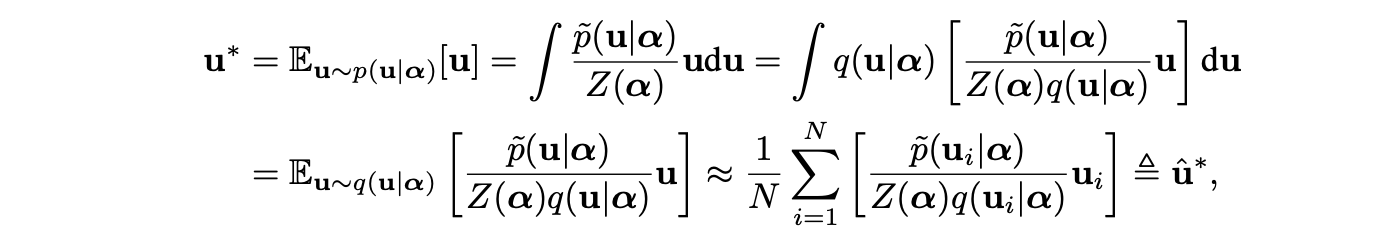
其中，由于分布 $的具体形式与损失函数有关难以确定，导致很难根据该分布进行采样。因此MGS使用了重要性采样的策略，即引入一个已知形式的分布，通过上式的策略将对分布的采样转化为对分布的采样。归一化系数同样可以按照下式获得：$

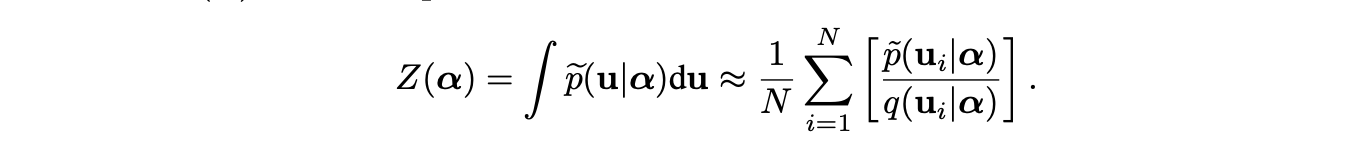
因此ZARTS-MGS中对架构参数的迭代公式为：$ α⟵α+u^∗ $ $。$

3 GradientLess Descent(GLD):

在每次迭代中，GLD提出使用预定义的更新量模值范围 $，早不同的半径的球面上对候选更新量进行采样，球面半径取值为 $ {2^{−k}R}_{k=0}^{log(R/r)} $。更新量通过下式得到：$

ZARTS-GLD中对架构参数的迭代公式为: $。$

下表整理了ZARTS的三种不同零阶优化实现。

此外，我们从理论上建立了 ZARTS 和 DARTS 之间的联系，表明在一阶/二阶近似的条件下，ZARTS可以退化为DARTS。详细推到请参考ZARTS论文。

为了验证零阶优化方法相比于梯度方法的优势，我们在可视化的损失函数等高线图上绘制了不同方法的优化路径：

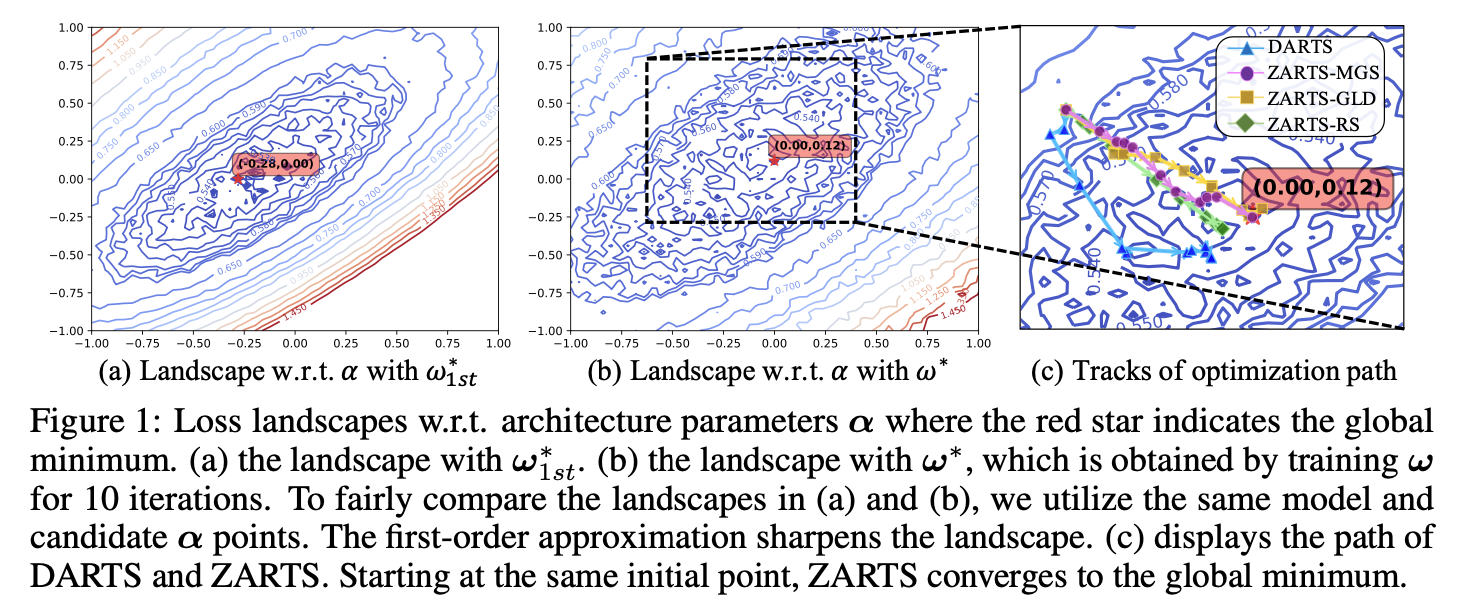
其中图c展示了DARTS与三种ZARTS形式的优化过程。为了公平比较，不同的方法从同样的起始点处开始，我们发现零阶优化方法（ZARTS）可以朝着更准确的方向（朝着最优点位置）更新，然后梯度方法（DARTS）却收敛到了偏离最优点的位置。

实验

1 稳定性实验

RobustDARTS[4]为了验证DARTS的搜索稳定性提出了四种小型搜索空间，试验发现DARTS在这四种搜索空间下很难搜索得到有效的结构。此外AmendedDARTS[5]提出对超网络进行长时间优化后（200 epochs），DARTS的结构会被skip-connection主导，同样存在不稳定问题。本文为了验证ZARTS的稳定性，分别按照RobustDARTS和AmendedDARTS的设定进行试验，结果分别入下表和下图所示。结果说明ZARTS具有很好的稳定性，在两种情况下均可以搜索得到有效的结构。

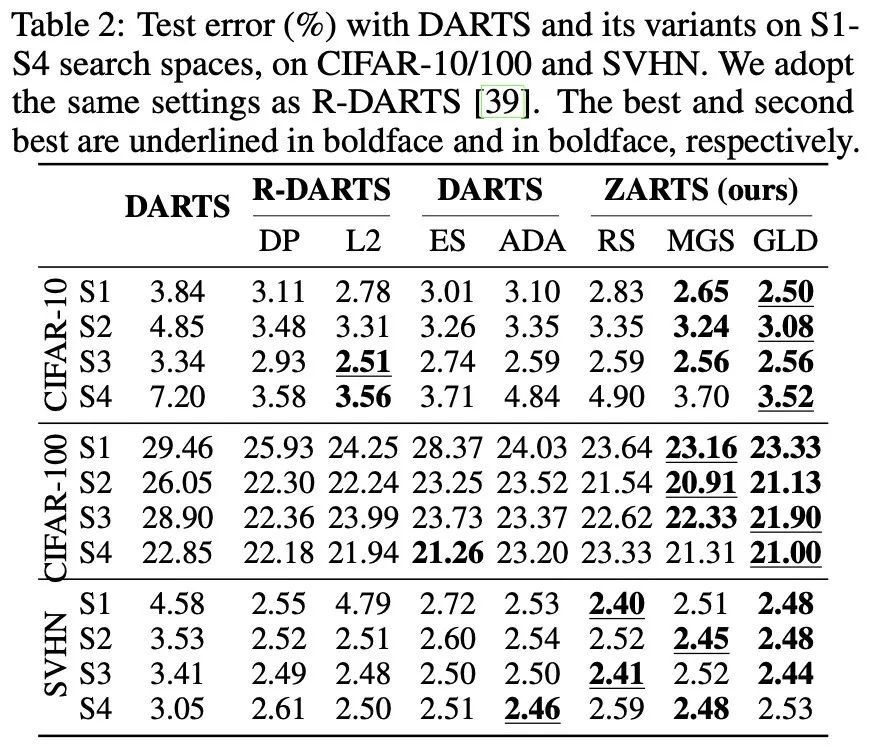
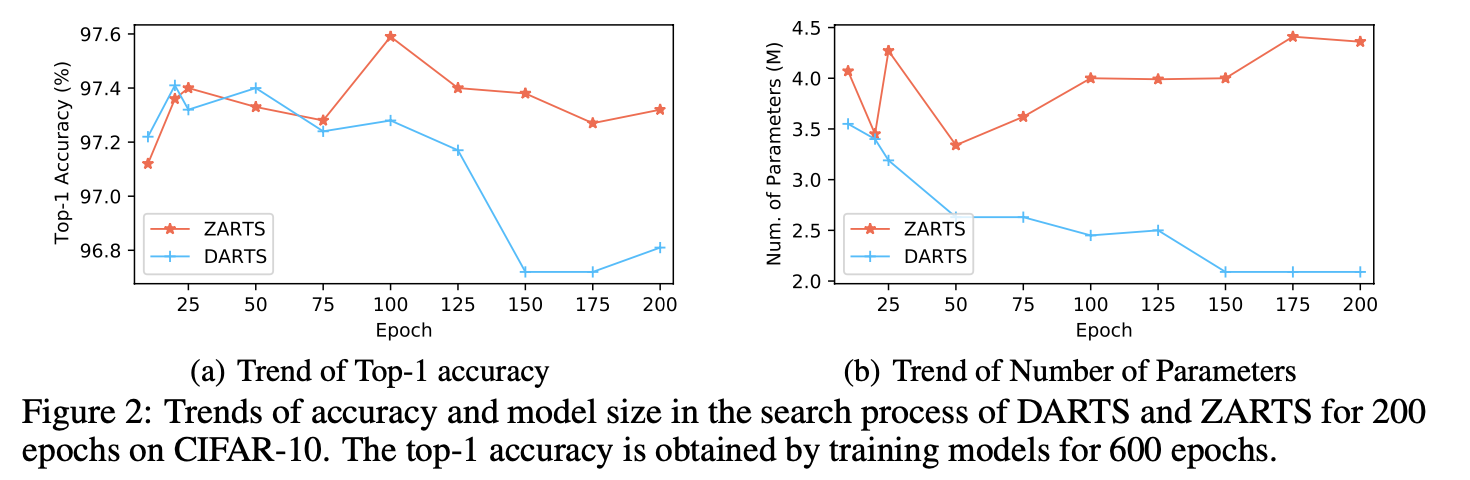
2 在DARTS标准搜索空间下的搜索结果

为了与DARTS及其变体方法进行比较，我们使用DARTS的标准搜索空间，分别在CIFAR-10和CIFAR-100数据集上进行搜索，结果如下图所示：

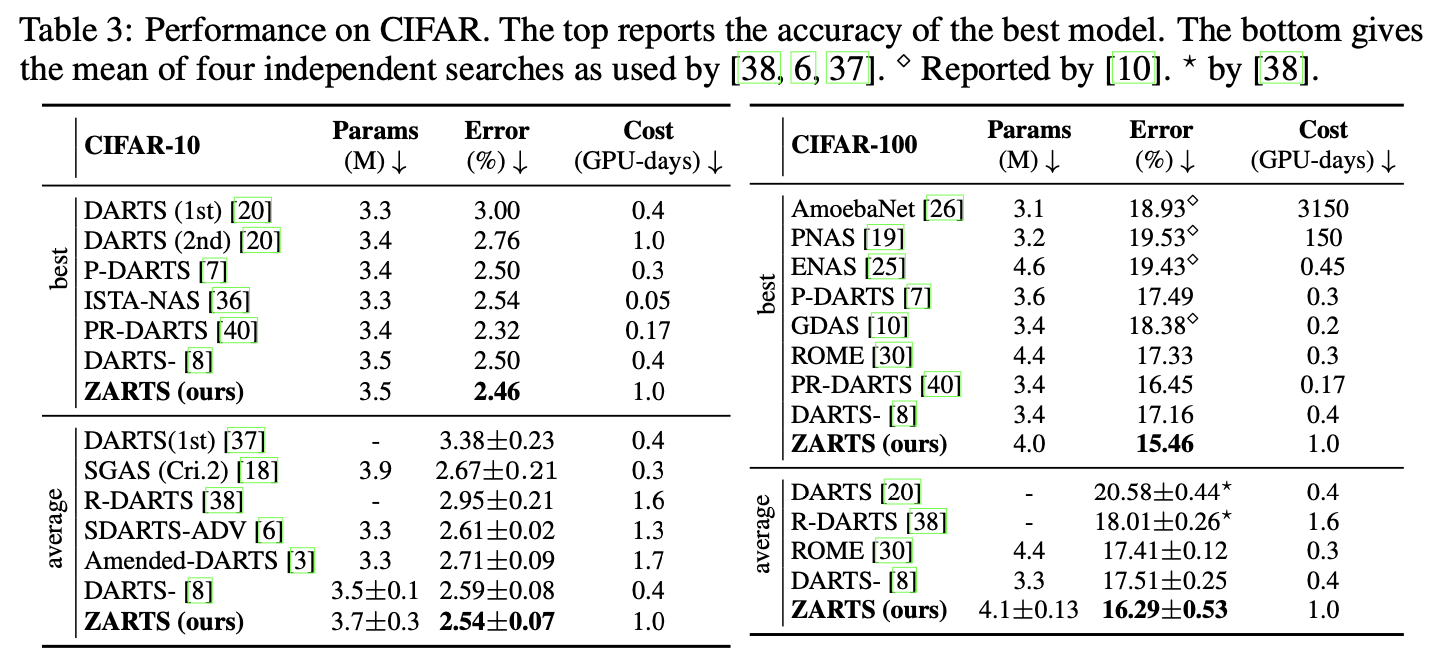
进一步，我们将搜索得到的结果迁移到ImageNet数据集上，同样展示出了很好的性能：

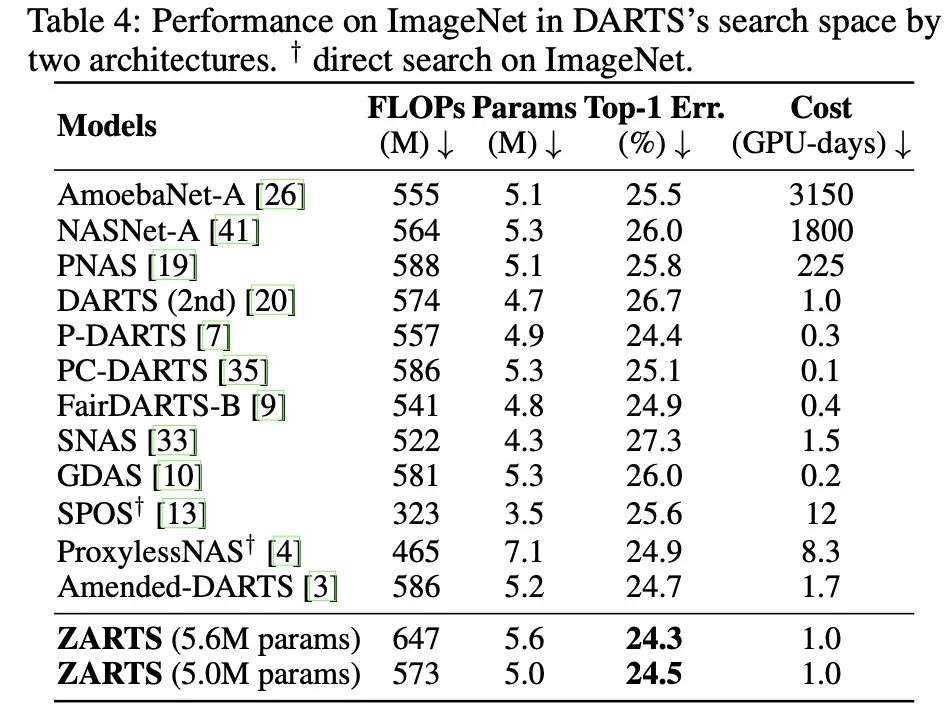
3 ZARTS的变体与加速

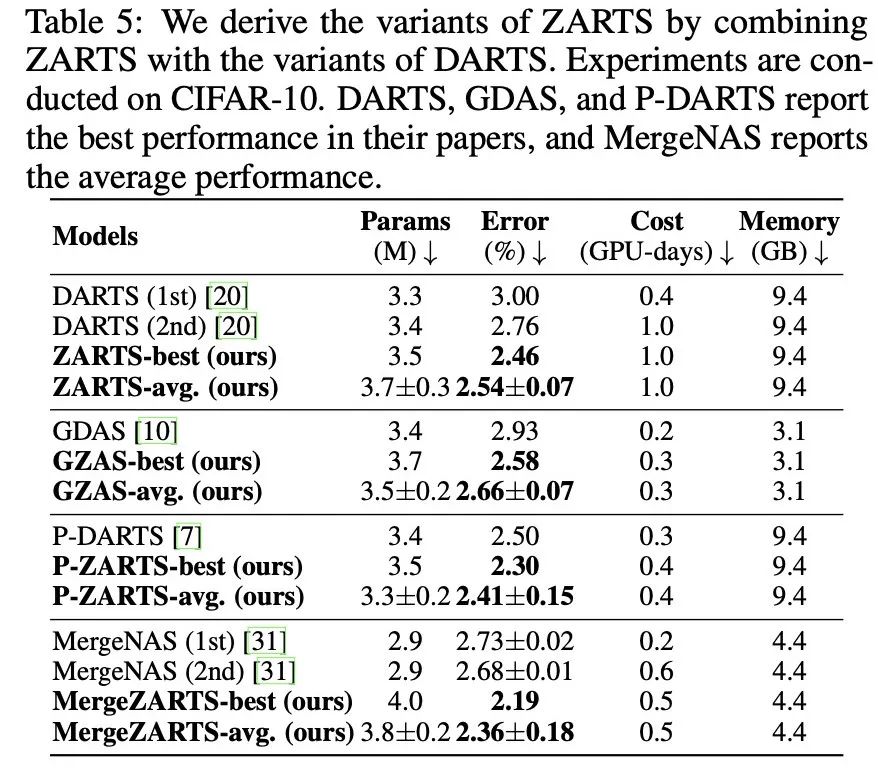
DARTS的很多变体方法可以加速搜索过程，且有更好的效果。由于ZARTS与DARTS的区别仅在于对架构参数 $的优化过程，因此很多DARTS的变体方法同样可以迁移到ZARTS上，起到加速和提升性能的作用。本工作将ZARTS与三种DARTS变体方法进行了结合：P-DARTS[6], GDAS[7], MergeNAS[8]。实验结果证明了上述分析：$

参考文献

Sijia Liu, Pin-Yu Chen, Bhavya Kailkhura, Gaoyuan Zhang, Alfred O Hero III, and Pramod K Varshney. A primer on zeroth-order optimization in signal processing and machine learning: Principals, recent advances, and applications. IEEE Signal Processing Magazine, 2020.
Welleck S, Cho K. Mle-guided parameter search for task loss minimization in neural sequence modeling. In AAAI, 2021.
Daniel Golovin, John Karro, Greg Kochanski, Chansoo Lee, Xingyou Song, and Qiuyi Zhang. Gradientless descent: High-dimensional zeroth-order optimization. In ICLR, 2020.
Arber Zela, Thomas Elsken, Tonmoy Saikia, Yassine Marrakchi, Thomas Brox, and Frank Hutter. Understanding and robustifying differentiable architecture search. In ICLR, 2020.
Kaifeng Bi, Changping Hu, Lingxi Xie, Xin Chen, Longhui Wei, and Qi Tian. Stabilizing darts with amended gradient estimation on architectural parameters. arXiv preprint arXiv:1910.11831, 2019.
Xin Chen, Lingxi Xie, Jun Wu, and Qi Tian. Progressive Differentiable Architecture Search: Bridging the Depth Gap between Search and Evaluation. In ICCV, 2019.
Xuanyi Dong and Yi Yang. Searching for a Robust Neural Architecture in Four GPU Hours. In CVPR, 2019.
Xiaoxing Wang, Chao Xue, Junchi Yan, Xiaokang Yang, Yonggang Hu, and Kewei Sun. Mergenas: Merge operations into one for differentiable architecture search. In IJCAI, 2020

内容中包含的图片若涉及版权问题，请及时与我们联系删除