作者苏剑林
在去年的文章《Transformer升级之路:博采众长的旋转式位置编码》中,笔者提出了旋转位置编码(RoPE),当时的出发点只是觉得用绝对位置来实现相对位置是一件“很好玩的事情”,并没料到其实际效果还相当不错,并为大家所接受,不得不说这真是一个意外之喜。
后来,在《Transformer升级之路:二维位置的旋转式位置编码》中,笔者讨论了二维形式的 RoPE,并研究了用矩阵指数表示的 RoPE 的一般解。
既然有了一般解,那么自然就会引出一个问题:我们常用的 RoPE,只是一个以二维旋转矩阵为基本单元的分块对角矩阵,如果换成一般解,理论上效果会不会更好呢?本文就来回答这个问题。
在《Transformer升级之路:二维位置的旋转式位置编码》中,我们将 RoPE 抽象地定义为任意满足下式的方阵
然后,我们探讨了如下矩阵指数形式的解
这里的矩阵指数,不是像 Softmax 那样的激活函数式的 element-wise 运算,而是按照泰勒级数定义的“Matrix Exponential”[1]。根据“Baker–Campbell–Hausdorff 公式”[2],我们有
这里 ,省略的都是 的三次或三次以上的项。按照式(1),那么上式指数部分应该等于 ,这就推出
进一步地,我们有 和 ,前者说明 是正交矩阵,后者则启示我们这是不是可以推广到任意正交矩阵?不难验证,答案是肯定的,我们有结论:
值得指出的是,在实数域内,并不是所有正交矩阵都可以写成 的形式,所以 实际上是比矩阵指数形式更宽泛的解。从《恒等式 det(exp(A)) = exp(Tr(A)) 赏析》[3] 中我们知道 ,所以能写成矩阵指数形式的正交矩阵行列式必然大于 0(即等于 1),事实上这个结果反过来也成立,即行列式等于 1 的正交矩阵,必然可以写成 的形式,其中 是反对称矩阵。(参考《Why can any orthogonal matrix be written as O=e^A》[4])。
而对于 的正交矩阵,我们有 ,其中 是对角线元素有一个-1、剩下都是1的对角阵, 则是 的正交矩阵,它可以写成 的形式,此时 。这也就是说,即便对于 的 ,也只是 的简单变换,所以接下来我们主要研究 形式的解。
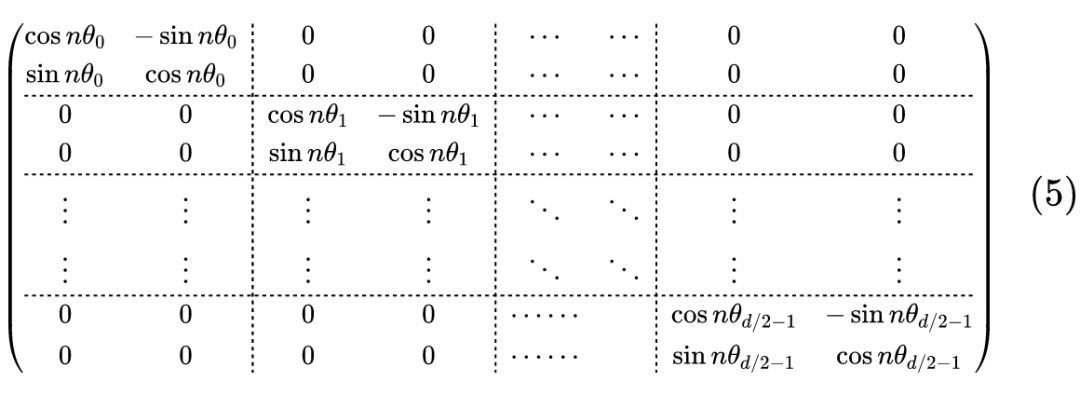
众所周知,我们平时所用的 RoPE 位置编码,是如下形式的分块对角矩阵:
这种选择可以说是最简单的一种,其本质原因可以说是为了降低计算量。那么,所谓完备性问题,就是要回答:如上的分块对角矩阵的特例,相比全参数 ,是否有能力上的缺失?换句话说,如果不考虑计算量,将 替换为一般的反对称矩阵,效果是否可能会有提升?
回答这个问题不困难,事实上,对于任意偶数阶反对称矩阵,它都可以对角化为分块对角矩阵
该结论可以参考 Skew-symmetric matrix [5]。也就是说,存在可逆矩阵 ,使得 ,于是
也就是说,任意的 与分块对角的 ,仅仅相差一个相似变换,而我们在 Self Attention 中应用 RoPE 时,是
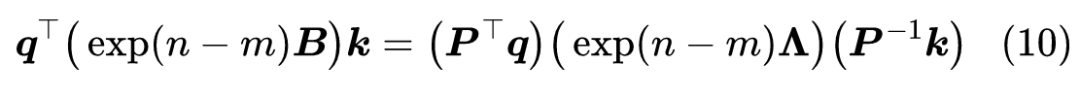
由于 一般都是输入 经过某个可学习的线性变换而来, 原则上都可以吸收到线性变换的训练参数中,因此直接设为 理论上不会损失一般性。
所以,对于 Self Attention 来说,问题的答案是否定的。不过,如果是线性 Attention,答案会有少许区别,因为线性 Attention 的 加了个激活函数:
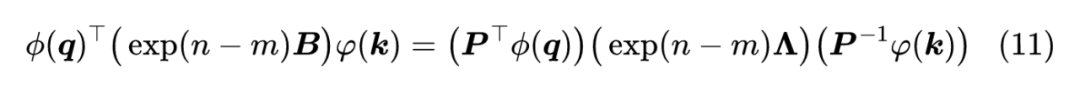
这就导致了 不一定能吸收到线性变换的训练参数中,因此对线性 Attention 补上两个参数矩阵,是有可能带来提升的。
本文简单分析了 RoPE 的完备性问题,表明对于 Self Attention 来说,目前的分块对角型 RoPE 不会损失一般性。
内容中包含的图片若涉及版权问题,请及时与我们联系删除
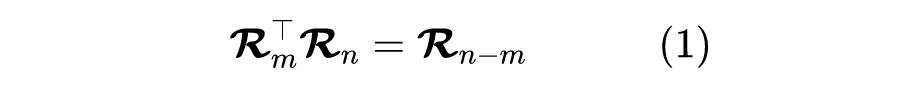
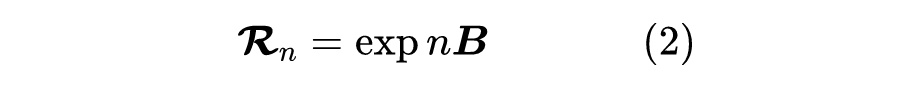
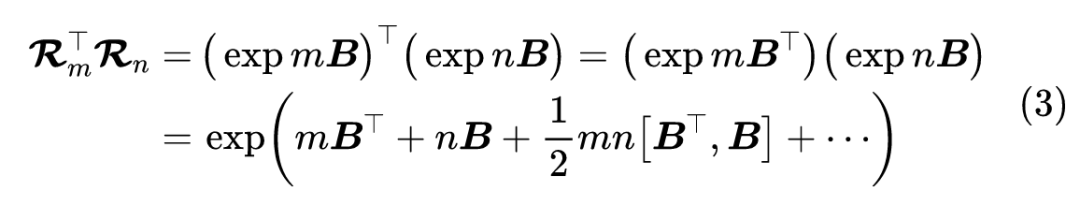
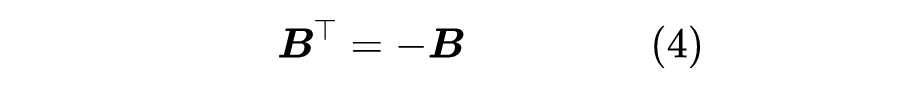
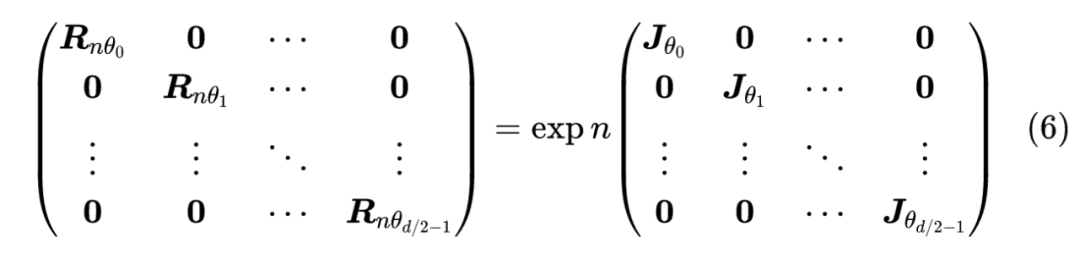
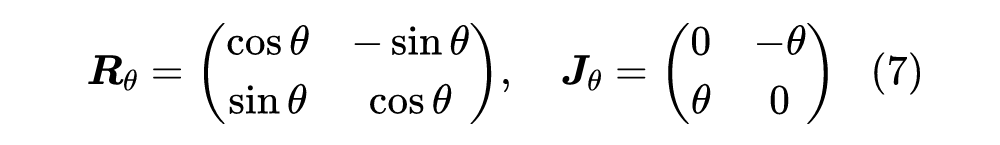
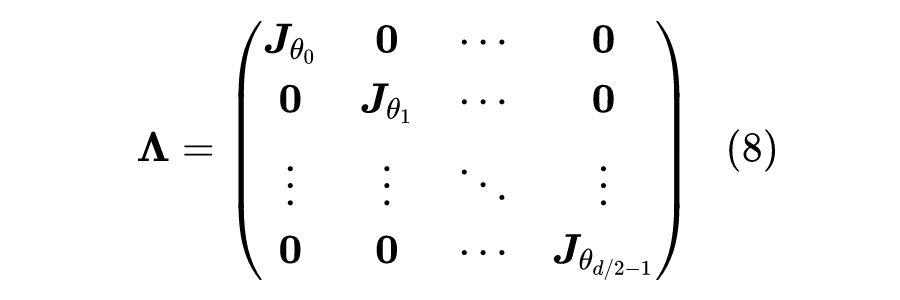
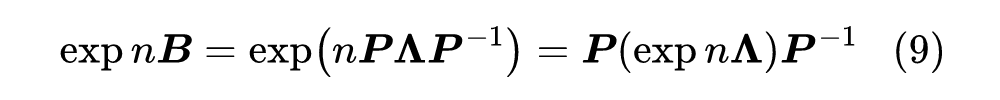
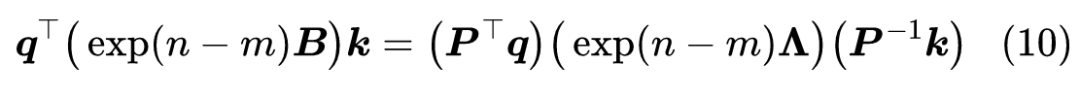
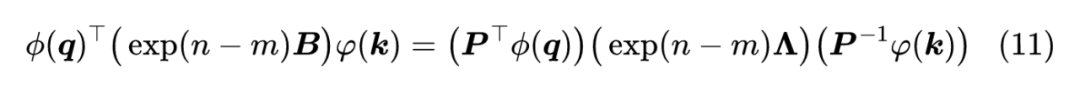



评论
沙发等你来抢