来自今天的爱可可AI前沿推介
[LG] Learning-Rate-Free Learning by D-Adaptation
A Defazio, K Mishchenko
[Meta AI & Samsung AI Center]
基于D-Adaptation的免学习率(非参数)学习
要点:
-
梯度下降的单环方法,不需要知道从初始点到解集的距离D,可渐近地实现凸 Lipschitz 函数复杂度类的最佳收敛率; -
式此类的第一个非参数方法,在收敛速率中没有额外的乘性对数因子; -
对该方法的 SGD 和 Adam 变体进行了广泛的实验,在十几个不同机器学习问题中能自动匹配手动微调的学习率,包括大规模视觉和语言问题。
一句话总结:
提出一种新的梯度下降方法,不需要知道到解集的距离 D,在不同机器学习问题中能匹配手动微调的学习率,每一步无需额外的函数值或梯度评估。
摘要:
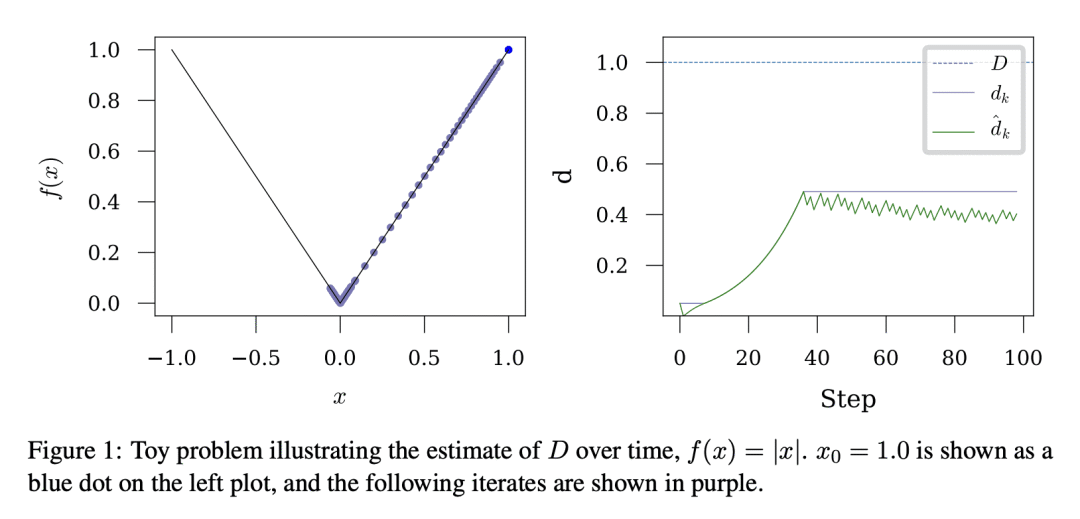
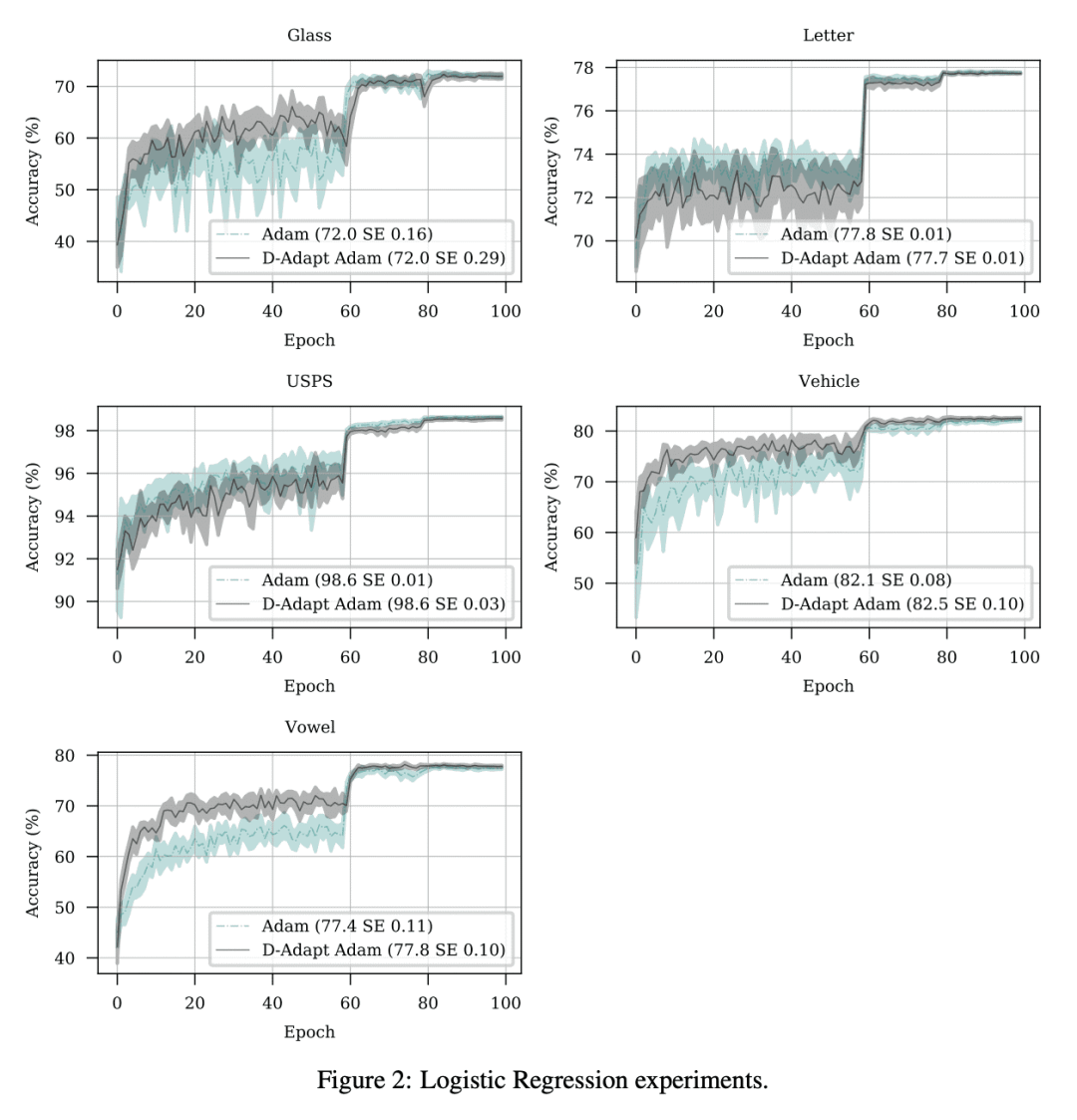
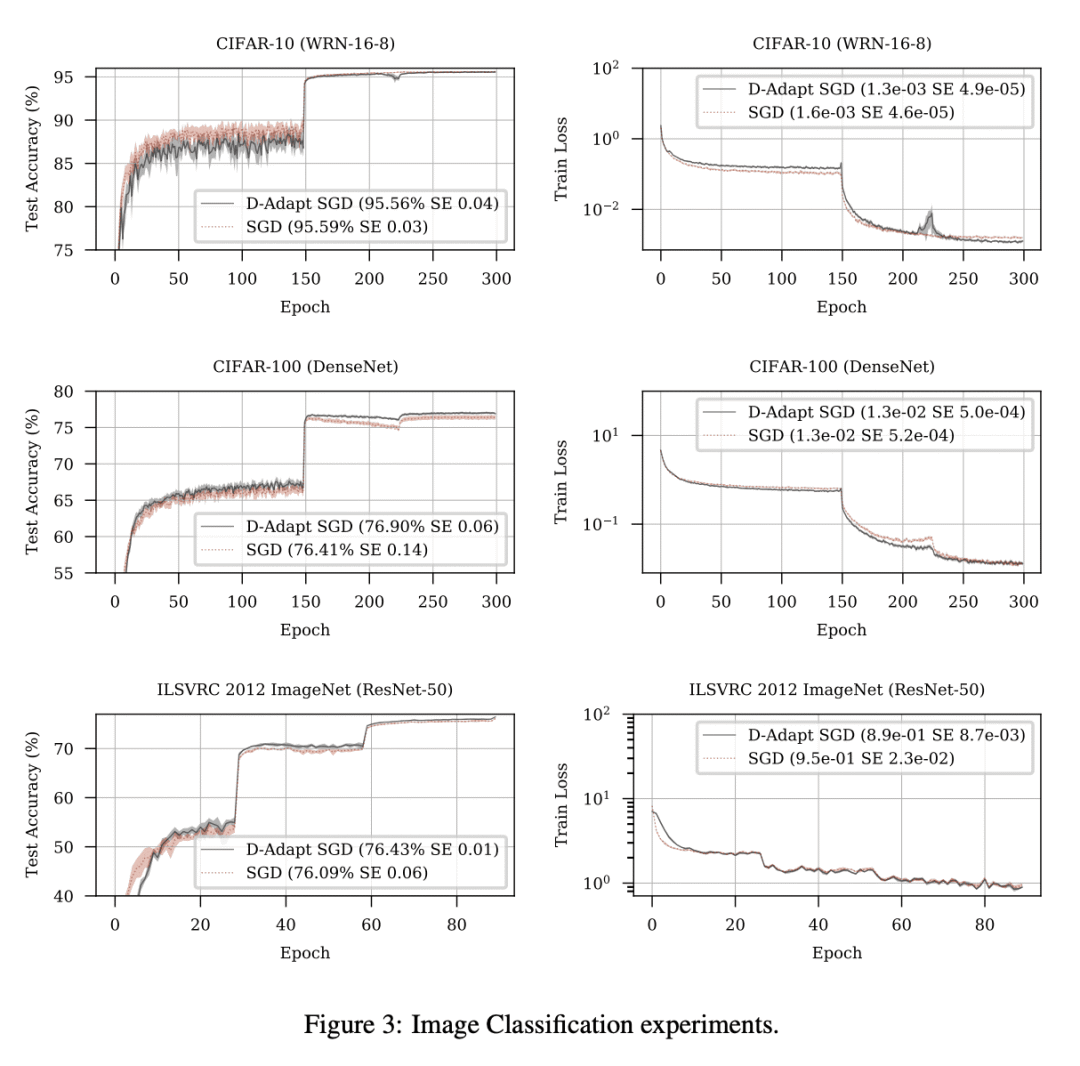
凸 Lipschitz 函数的梯度下降速度,在很大程度上取决于学习率的选择。设置学习率以实现最佳收敛率,需要知道从初始点到解集的距离D。本文描述了一种单循环方法,无需回溯或线搜索,不需要关于 D 的知识,但渐近地实现了凸 Lipschitz 函数复杂类的最佳收敛速度。该方法是此类的第一个无参数方法,在收敛速率中没有额外的乘性对数因子。对该方法的 SGD 和 Adam 变体进行了广泛的实验,在十几个不同的机器学习问题(包括大规模视觉和语言问题)中能自动匹配手动微调的学习率。该方法实用、高效,每一步不需要额外的函数值或梯度评估。
The speed of gradient descent for convex Lipschitz functions is highly dependent on the choice of learning rate. Setting the learning rate to achieve the optimal convergence rate requires knowing the distance D from the initial point to the solution set. In this work, we describe a single-loop method, with no back-tracking or line searches, which does not require knowledge of D yet asymptotically achieves the optimal rate of convergence for the complexity class of convex Lipschitz functions. Our approach is the first parameter-free method for this class without additional multiplicative log factors in the convergence rate. We present extensive experiments for SGD and Adam variants of our method, where the method automatically matches hand-tuned learning rates across more than a dozen diverse machine learning problems, including large-scale vision and language problems. Our method is practical, efficient and requires no additional function value or gradient evaluations each step.
论文链接:https://arxiv.org/abs/2301.07733
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢