【隐私计算笔谈】MPC系列专题（十一）：共享随机数和比特分享

本次科普主要介绍多方比较的实现方法。回忆一下，之前介绍过的Shamir(t,n)秘密分享协议可以实现秘密分享，Shamir(t,n)协议主要基于拉格朗日插值，也可以通俗地理解成𝑛个方程求解𝑛个未知数。

BGW协议可以实现单比特分享，本次要介绍另一个比特分享方式。利用比特分享的方式，可以对𝑙比特的一个数按比特进行多方分享，之后可以据此实现多方比较。多方比较则可以用来构造安全多方计算的基础模块，无论是隐私保护的机器学习还是隐私保护的DNA比较等，都需要用到多方比较模块。

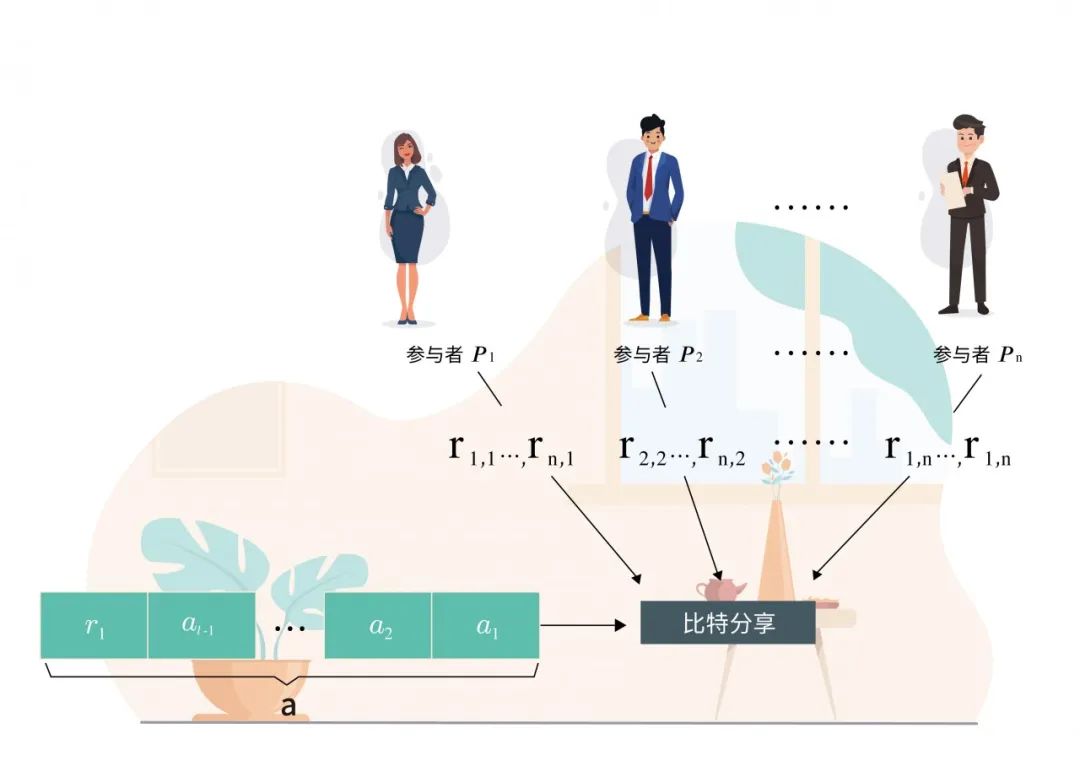
按比特分享

如有一个比特串𝑎 =𝑎_𝑙𝑎_𝑙-1…𝑎₁，𝑎₁到𝑎_𝑙分别是组成𝑎的各个比特，即𝑎的值为。对𝑎进行比特分享即对𝑎的各个比特进行分享，每个参与者拿到𝑎₁,…,𝑎_𝑙的𝑙个子秘密。将参与者𝑃_𝑖拿到的𝑎_𝑗的子秘密记为𝑎_𝑗,𝑖，则对𝑙比特长的𝑎进行比特分享后参与者𝑃_𝑖能够获得𝑎_1,𝑖,𝑎_2,𝑖,…,𝑎_𝑙,𝑖。 

首先简要介绍一个多个参与者共同产生同一个随机数的方式：假设有𝑛个参与者𝑃₁,…,𝑃_𝑛，每个参与者𝑃_𝑖都产生一个随机数𝑟_𝑖，并通过Shamir(t,n)秘密分享机制将𝑟_𝑖进行分享，记𝑟_𝑖,𝑗为参与者𝑃_𝑗获得的𝑟_𝑖的子秘密。因此当每个参与者都产生随机数并分享后，参与者𝑃_𝑖可以获得𝑟_1,𝑖,…,𝑟_𝑛,𝑖。

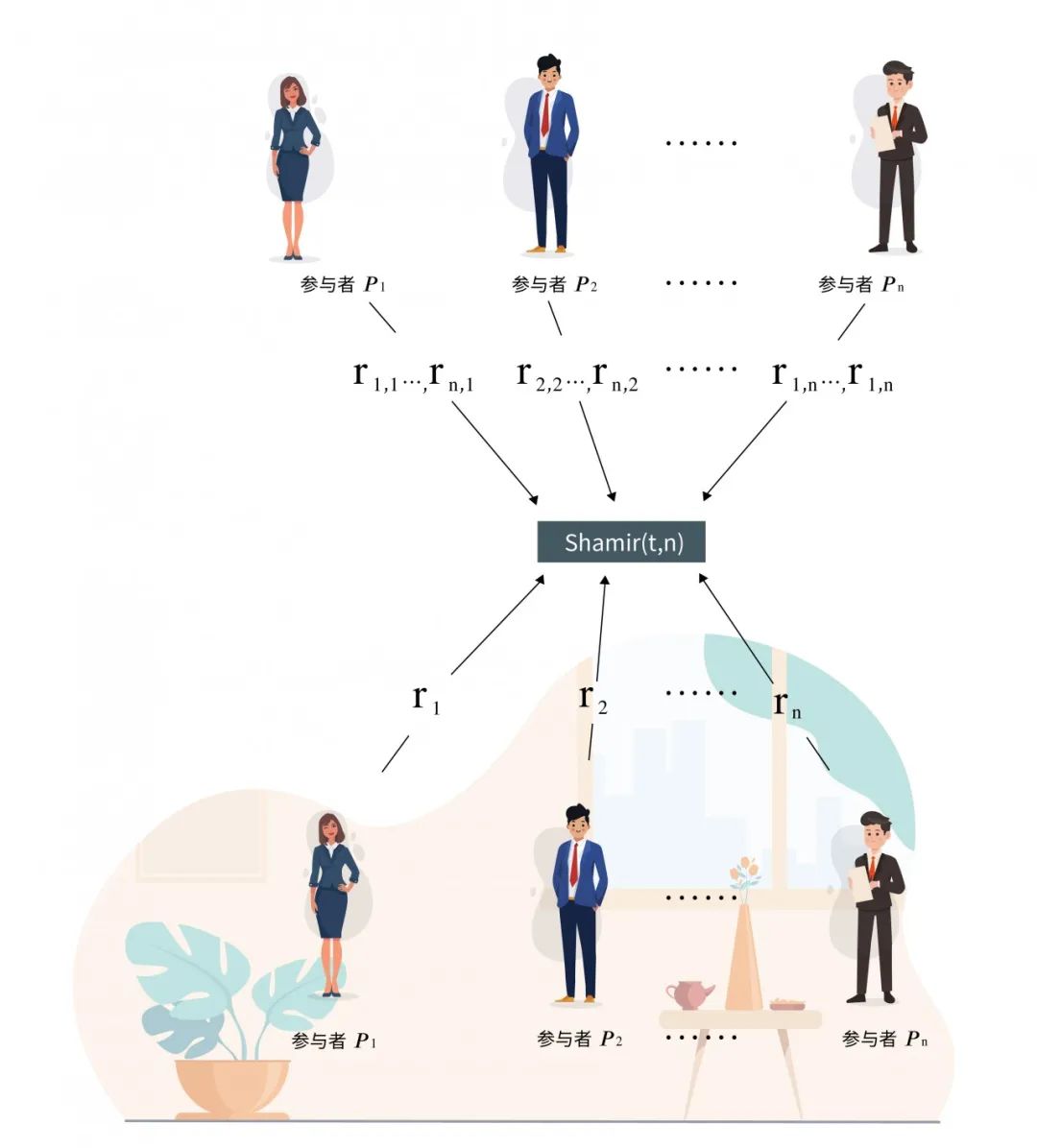
多方随机数生成

参与者𝑃_𝑖获得子秘密𝑟_1,𝑖,…,𝑟_𝑛,𝑖之后，将它们进行累加，将累加结果记为𝑟_𝑖'，。用符号𝑟表示𝑟₁,…,𝑟_𝑛之和，即，则𝑟_𝑖'就是𝑟的一个子秘密。因为𝑟_1,𝑖是𝑟₁的一个子秘密，𝑟_𝑗,𝑖是𝑟_𝑖的一个子秘密，由于Shamir(t,n)具有可加性（在第二次科普中介绍过）。假设参与者𝑃₁的𝑟₁的秘密分配函数是𝑓₁(𝑥) =𝑎_t-1𝑥^t-1+⋯+𝑎₁𝑥+𝑟₁，参与者𝑃₂的𝑟₂的秘密分配函数是𝑓₂(𝑥)=𝑏_t-1𝑥^t-1+⋯+𝑏₁𝑥+𝑟₂，则参与者𝑃₁和𝑃₂分配给参与者𝑃_𝑗的子秘密分别为𝑟_1,𝑗=𝑓₁(𝑗)和𝑟_2,𝑗=𝑓₂(𝑗)，二者相加为：𝑟_1,𝑗+𝑟_2,𝑗=𝑓₁(𝑗)+𝑓₂(𝑗)=(𝑎_t-1+𝑏_t-1)𝑗^t-1+⋯+(𝑎₁+𝑏₁)𝑗+𝑟₁+𝑟₂，即𝑟_1,𝑗+𝑟_2,𝑗也是𝑟₁+𝑟₂的一个子秘密，𝑟_1,1+𝑟_2,1,𝑟_1,2+ 𝑟_2,2,…,𝑟_1,𝑛+𝑟_2,𝑛也是𝑟₁+𝑟₂的子秘密。同理𝑟₁'=𝑟_1,1+⋯+𝑟_𝑛,1, 𝑟₂'=𝑟_1,2+⋯+𝑟_𝑛,2, 𝑟_𝑛'=𝑟_1,𝑛+⋯+𝑟_𝑛,𝑛是的子秘密。 

注意此时每个参与者𝑃_𝑖都不知道其他参与者产生的随机数𝑟_𝑗，因此参与者𝑃_𝑖也无法计算出𝑟的具体值，但是他通过计算可以计算出𝑟的一个子秘密𝑟_𝑖'。通过每个参与者都产生一个随机数并进行秘密共享，所有参与者共同协作产生了一个随机数，但是每个参与者𝑃_𝑖都不知道𝑟的具体值，都只掌握𝑟的一个子秘密𝑟_𝑖'。

在学习了多方共同产生随机数后，可以利用此来实现多方的随机单比特分享，每个参与者拿到一个随机比特的Share，在重构之前每个参与者都不知道该随机比特的具体值。首先所有参与者利用上节所讲述的共享随机数生成方式共同生成一个随机数，将其记为𝑟，将参与者𝑃_𝑖拿到的𝑟的子秘密记为𝑟_𝑖'（保持与上节的符号统一），用[𝑟]表示𝑟处于被分享成子秘密的状态，[𝑟]由𝑟₁',…,𝑟_𝑛'组成。

之后通过第二次科普介绍的Shamir多方乘法，计算[𝑟²]，参与者𝑃_𝑖能够计算出𝑟²的一个子秘密。之后所有参与者分享自己计算出的𝑟²的子秘密，即公开[𝑟²]，每个参与者通过公开的[𝑟²]都可使用拉格朗日插值法重构出𝑟²，若重构出的𝑟²=0则各方再重新生成随机数𝑟。

参与者𝑃_𝑖在计算出𝑟²后，计算𝑟= ，由于这些操作都是在有限域𝐹_𝑞内进行，因此0<𝑟<𝑞，此时能够计算出两个𝑟′′，𝑟′′=𝑞−𝑟或𝑟′′=𝑟。则(𝑟′′)^-1的逆乘上𝑟有两种结果，(𝑟′′)^-1𝑟=𝑞−1或者(𝑟′′)^-1𝑟=1。因为𝑟′′∙(𝑟′′)^-1=1，当𝑟′′=𝑟时，(𝑟′′)^-1𝑟=𝑟^-1𝑟=1；当𝑟′′=𝑞−𝑟时，(𝑟′′)^-1𝑟= (−𝑟)^-1𝑟 =(−1)∙𝑟^-1𝑟=𝑞−1。, 参与者可以约定选取0<𝑟′′<，那么所有参与者就可以计算出相同的𝑟′′，参与者𝑃_𝑖设置𝑟^-1=(𝑟′′)^-1

对于参与者𝑃_𝑖来说，𝑃_𝑖掌握𝑟的子秘密𝑟_𝑖'，𝑃_𝑖设置𝑎_𝑖=2^-1((𝑟^-1)𝑟_𝑖'+1)，𝑎_𝑖即为𝑃_𝑖获得的随机比特𝑎的一个子秘密。因为参与者𝑃_𝑖只知道𝑟，对于𝑃_𝑖来说𝑟依旧有两种可能，分别是± ，因此𝑃_𝑖无法确定𝑎的值是0还是1，只有所有参与者对𝑟进行重构才能确定𝑟的值，从而计算出𝑎。𝑟是所有参与者共同产生的随机数，因此𝑎的值也是随机的，且在重构之前每个参与者都只掌握随机比特𝑎的一个子秘密，不知道𝑎的具体值。