来自今天的爱可可AI前沿推介
[LG] A theory of continuous generative flow networks
S Lahlou, T Deleu, P Lemos, D Zhang, A Volokhova, A Hernández-García, L N Ezzine, Y Bengio, N Malkin
[Mila & Universite de Montreal & Ciela Institute]
连续生成流网络理论
要点:
-
提出一种包含离散和连续状态空间的广义生成流网络理论; -
流匹配、详细平衡和轨迹平衡条件的扩展; -
一个定理,证明当这些条件中的任何一个得到满足时,学到的前向核从目标分布中采样。
一句话总结:
提出一个广义生成流网络(GFlowNet)理论,涵盖了离散和连续/混合状态空间。
摘要:
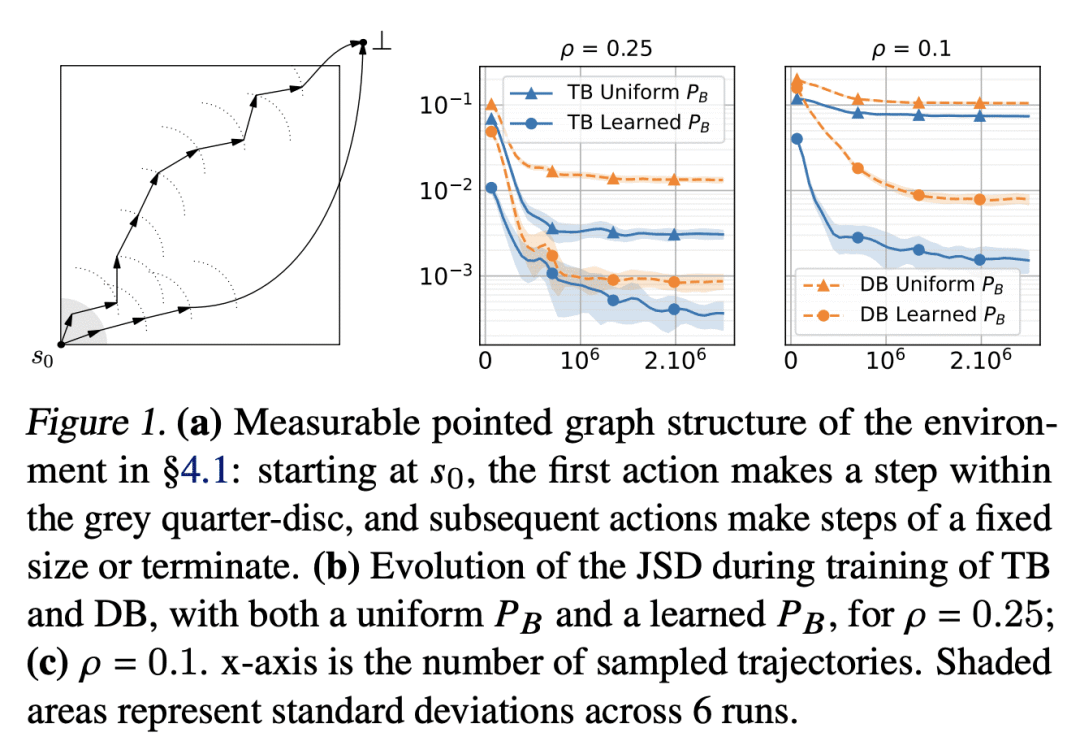
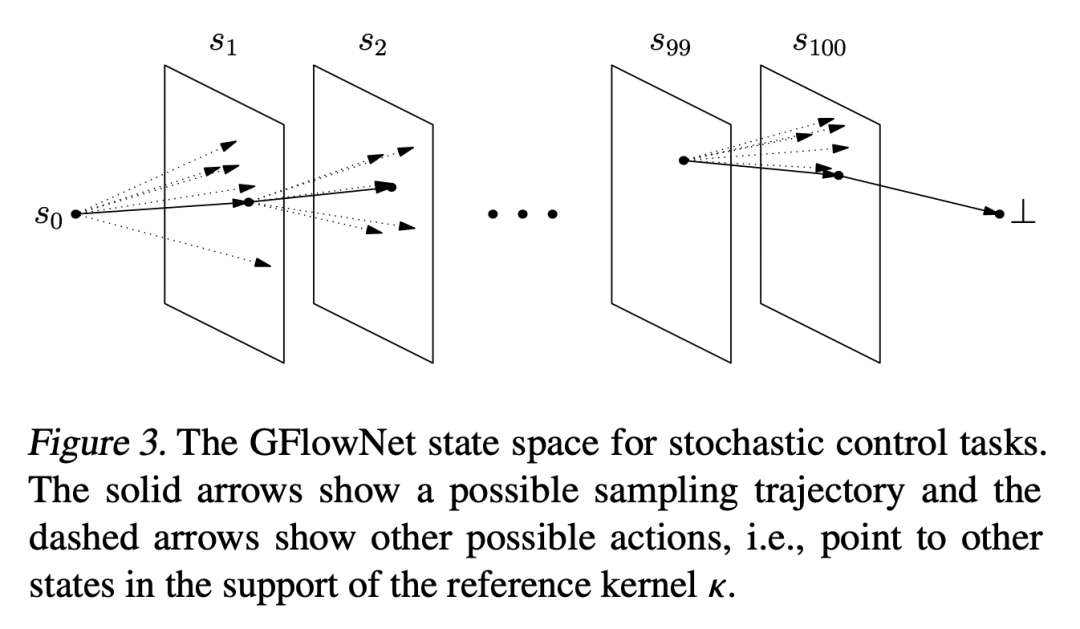
生成式流网络(GFlowNet)是一种摊销的变分推理算法,它被训练成从组成对象的非标准化目标分布中取样。到目前为止,GFlowNet 的一个关键局限,是被限制在离散空间。本文提出一个广义 GFlowNet 理论,其中包括现有的离散 GFlowNet 和具有连续或混合状态空间的 GFlowNet,并以两个目标进行了实验。说明了该理论的关键点和各种假设的重要性,从经验上证明了关于离散的 GFlowNet 的观察是如何迁移到连续的情况下的,并且在几个之前研究的任务上显示了与非 GFlowNet 基线相比的强大结果。本文工作大大拓宽了 GFlowNet 在概率推理和各种建模环境中的应用前景。
Generative flow networks (GFlowNets) are amortized variational inference algorithms that are trained to sample from unnormalized target distributions over compositional objects. A key limitation of GFlowNets until this time has been that they are restricted to discrete spaces. We present a theory for generalized GFlowNets, which encompasses both existing discrete GFlowNets and ones with continuous or hybrid state spaces, and perform experiments with two goals in mind. First, we illustrate critical points of the theory and the importance of various assumptions. Second, we empirically demonstrate how observations about discrete GFlowNets transfer to the continuous case and show strong results compared to non-GFlowNet baselines on several previously studied tasks. This work greatly widens the perspectives for the application of GFlowNets in probabilistic inference and various modeling settings.
论文链接:https://arxiv.org/abs/2301.12594

内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢