来自今天的爱可可AI前沿推介
[LG] Efficient Graph Field Integrators Meet Point Clouds
K Choromanski, A Sehanobish, H Lin, Y Zhao, E Berger…
[Google Research & Columbia University & Haifa University & Stanford University & …]
点云与高效图场积分器
要点:
-
提出两类新算法,SeparatorFactorization (SF) 和 RFDiffusion (RFD),用于在编码点云的图上进行有效的场积分; -
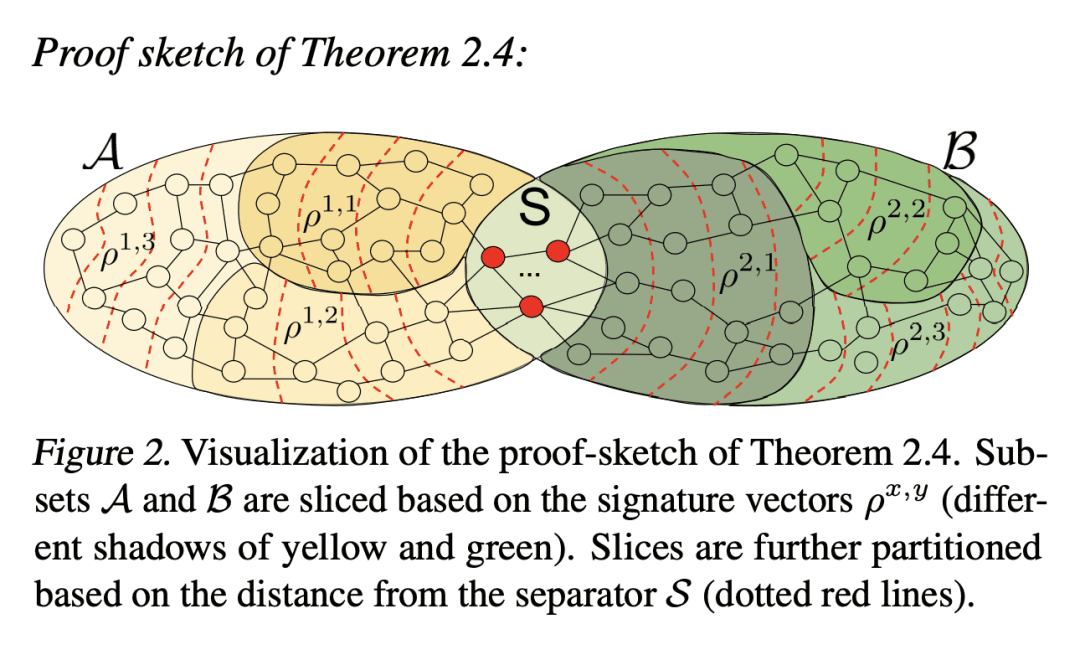
SF利用了点云网图的有界属性,对近似的图场积分具有 O(N log2(N)) 的时间复杂度,在某些特殊情况下有额外的计算收益; -
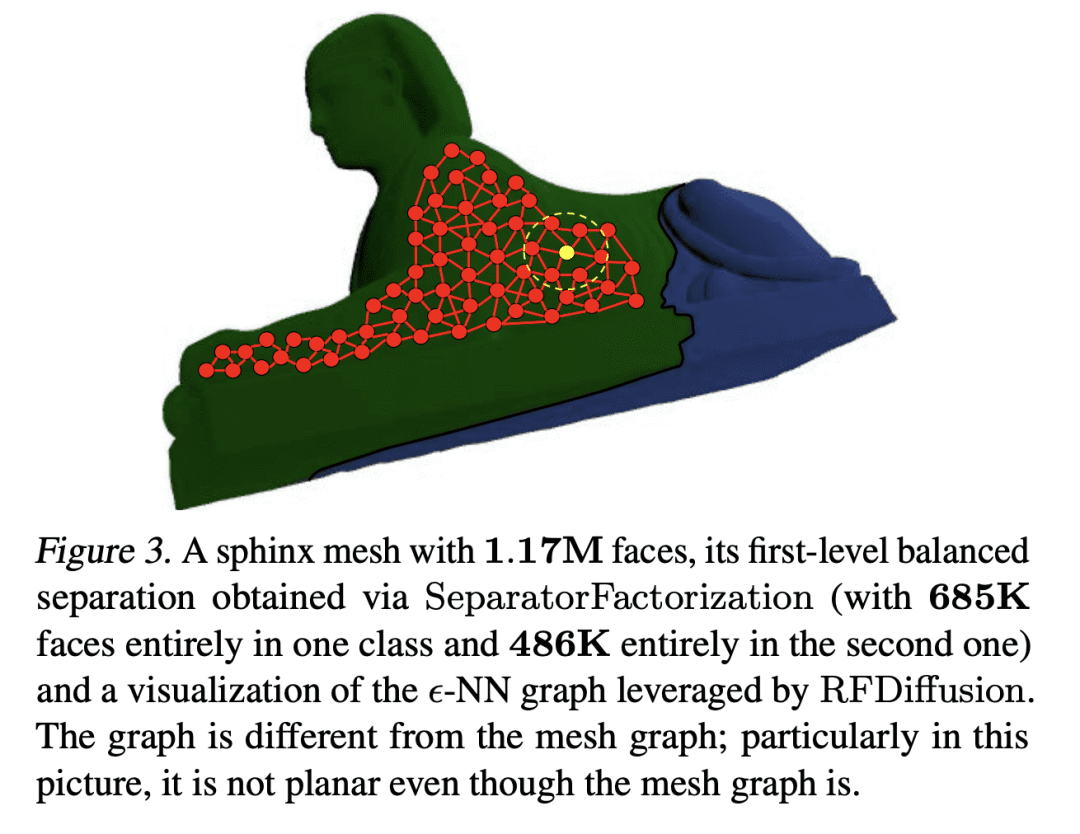
RFD 使用 epsilon-nearest-neighbor 图表示,对近似图场积分来说,具有 O(N) 的时间复杂度,利用了基于随机特征嵌入。
一句话总结:
提出两种在编码点云的图上进行高效场积分的算法,利用网图的有界性及epsilon-nearest-neighbor图表示,并对其有效性进行了广泛的理论分析和经验评估。
摘要:
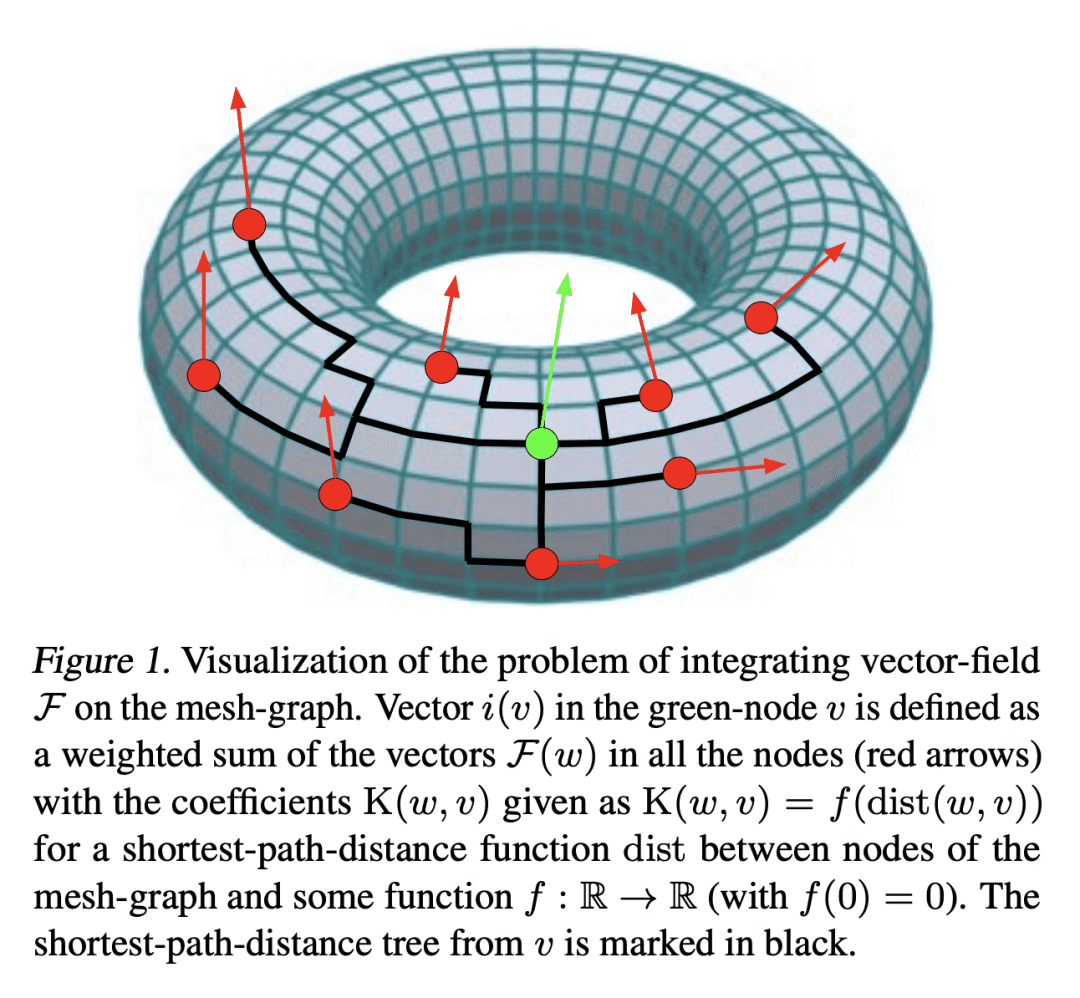
本文提出两类新的算法,用于在编码点云的图上进行有效的场积分。第一类,SeparatorFactorization(SF),利用点云网图的有界属性,第二类,RFDiffusion(RFD),用流行的 epsilon-nearest-neighbor 图来表示点云。两者都可以看作是提供了快速多极方法(FMM)的功能,这些方法对高效积分产生了巨大的影响,但是是对于非欧几里得空间而言。本文专注于由点与点之间的漫游长度分布(例如,最短路径距离)所引起的几何形状。对所提出的算法进行了广泛的理论分析,作为副产品获得了结构图论的新结果。本文还进行了详尽的经验评估,包括刚性和可变形物体的表面插值(特别是用于网格动力学建模),点云的 Wasserstein 距离计算,以及 Gromov-Wasserstein 变体。
We present two new classes of algorithms for efficient field integration on graphs encoding point clouds. The first class, SeparatorFactorization(SF), leverages the bounded genus of point cloud mesh graphs, while the second class, RFDiffusion(RFD), uses popular epsilon-nearest-neighbor graph representations for point clouds. Both can be viewed as providing the functionality of Fast Multipole Methods (FMMs), which have had a tremendous impact on efficient integration, but for non-Euclidean spaces. We focus on geometries induced by distributions of walk lengths between points (e.g., shortest-path distance). We provide an extensive theoretical analysis of our algorithms, obtaining new results in structural graph theory as a byproduct. We also perform exhaustive empirical evaluation, including on-surface interpolation for rigid and deformable objects (particularly for mesh-dynamics modeling), Wasserstein distance computations for point clouds, and the Gromov-Wasserstein variant.
论文链接:https://arxiv.org/abs/2302.00942
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢