【隐私计算笔谈】MPC系列专题（十二）：比特比较

上次的科普介绍了共享随机数和比特分享，通过共享随机数来实现比特分享，再通过比特分享来实现本次要介绍的比特串比较。

在介绍比特比较之前先简单介绍一下比特的或。比特异或的实现方法较为简单，利用之前介绍过的𝐹₂下Shamir共享机制的加法就能实现。而比特或则无法直接通过Shamir共享机制的加法或者乘法实现。

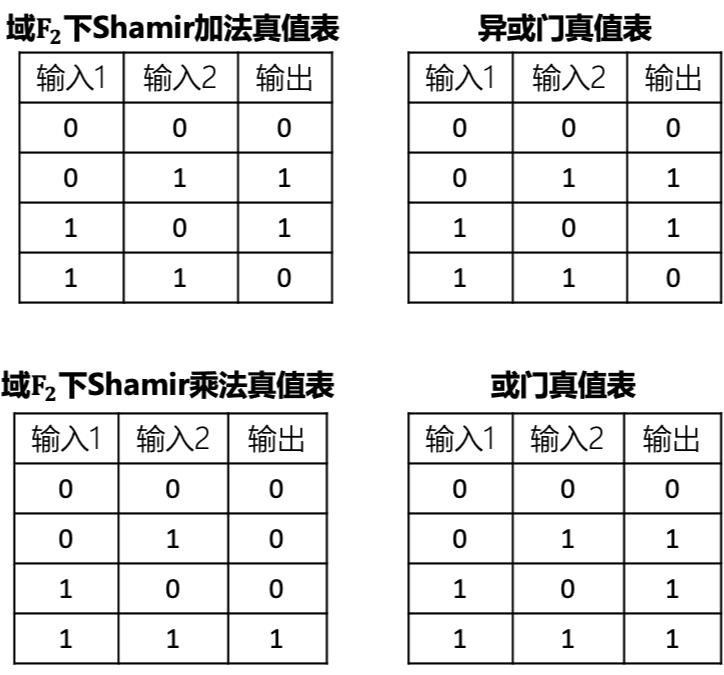
注意之前介绍过，在算数电路上实现乘法和加法即可实现任意函数，而在布尔电路上实现异或和与即可实现任意函数。安全多方计算就是为了在保护隐私信息下共同计算目标函数，如果把比特与通过使用加法和乘法的函数表示，那么即可通过加法和乘法实现与门的功能。 

思考一下与的特点，当多个比特相或时，其中只要有一个比特的值为1，或的结果就是1，因此可以统计出现1的个数，只要超过0次，最后的值就为1。可以设计出这样一个函数：若函数有个𝑙输入，分别为𝑥₁,…,𝑥_𝑙，则让，让实现与的函数为𝑓(𝑥₁,…,𝑥_𝑙)： 

将，是因为当时会泄露信息。回忆一下，在Shamir秘密分享机制中，当秘密分享函数的输入为0时，得到的就是秘密，因此需要避免输入为0。让可以使得函数𝑓(𝑔)的定义域从[0,𝑙]变为[1,𝑙+1]，从而避免出现输入𝑔为0的情况。𝑓(𝑔)的具体实现则可通过有𝑛个未知系数的方程，𝑛个方程解𝑛个未知数即可，即𝑓(1)=0,𝑓(2)=⋯=𝑓(𝑙+1)=1。把和𝑓(𝑔)映射到Shamir秘密共享机制上，加法和乘法对应Shamir中的加和乘，即可实现在共享的比特上的或计算。 

具体要介绍的比较为小于，即如果比特串𝑎<𝑏，则得到的结果为1，如果𝑎>𝑏，则得到的结果为0。假设有两个𝑙比特长的比特串𝑎和𝑏，分别为𝑎=𝑎₀𝑎₁⋯𝑎_𝑙-1和𝑏=𝑏₀𝑏₁⋯𝑏_𝑙-1，首先将比特串𝑎和𝑏按比特进行异或，得到比特串𝑐=𝑐₀⋯𝑐_𝑙-1，其中𝑐_𝑖=𝑎_𝑖⨁𝑏_𝑖,0≤𝑖≤𝑙−1。再计算比特串𝑑=𝑑₀⋯𝑑_𝑙-1，其中,0≤𝑗≤𝑙−1，即比特串𝑑的第𝑗位比特是比特串𝑐从高位起前𝑗位比特的或。

比如，如果比特串𝑎=100 101 ，比特串𝑏=101 011，比特串𝑐为比特串𝑎和𝑏按位异或的结果，比特串𝑐=001 110，比特串，可以得到比特串𝑑=001 111。比特串𝑑的第𝑗位比特是比特串𝑐从高位起前𝑗位比特的或，可以观察到当比特串𝑐中某个比特是整个比特串中第一位为1的时候，比特串𝑑从那位起之后都为1。如以上举的例子中，𝑐₃为比特串𝑐中第一个出现1的比特，则比特串𝑑的𝑑₃以及𝑑₃之后都为1，之前都为0。

再接着让𝑒_𝑗=𝑑_𝑗-1−𝑑_𝑗, 1≤𝑗≤𝑙−1, 𝑒₀=𝑑₀，因此可以得到比特串𝑒，在上面这个例子中，得到的比特串𝑒=001 000，即比特串𝑒会保留比特串𝑑中第一位出现1的那位，其余位均为0。

最后，计算即为最后的结果，在上面这个例子中结果为1，和比特串𝑎<𝑏相符合。

它所使用的原理是，如果比特串𝑏>𝑎，那么比特串𝑏中第一位1出现的一定比比特串𝑎中的第一位1要早，否则比特串𝑏就小于等于比特串𝑎。

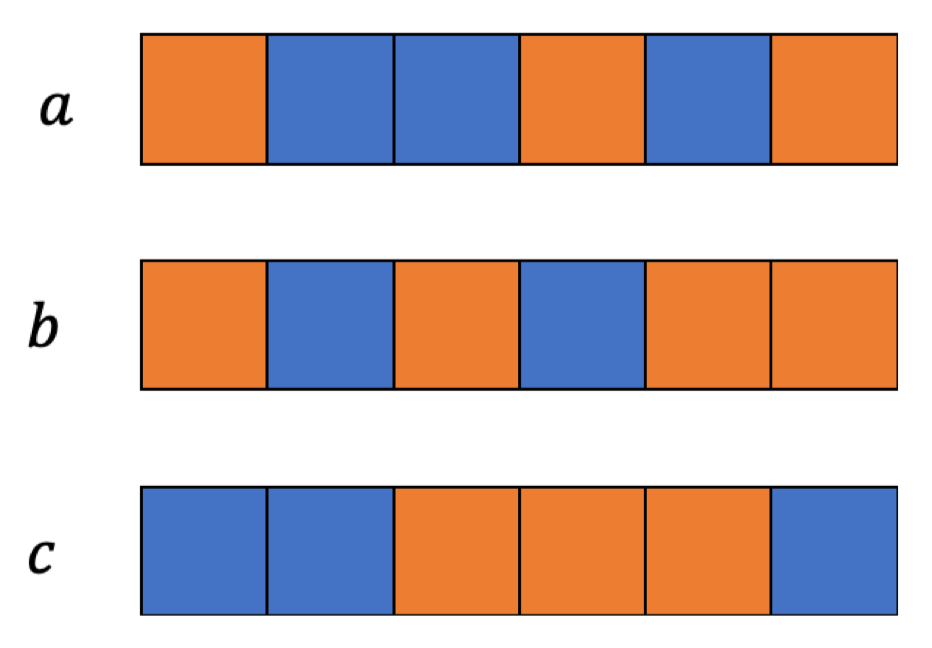
将比特串𝑎和𝑏按位进行异或得到𝑐后，比特串𝑐中第一位1出现的位置就是比特串𝑎和𝑏中最早的第一位1出现的位置。那么如果比特串𝑐中第一位1出现的位置和𝑏中最早的第一位1出现的位置相同，就说明𝑏>𝑎。而接下去做的步骤就是为了证明比特串𝑐中第一位1出现的位置和𝑏中最早的第一位1出现的位置是否相同。在上面的例子中，用橘色表示1，蓝色表示0，则𝑎、𝑏、𝑐为： 

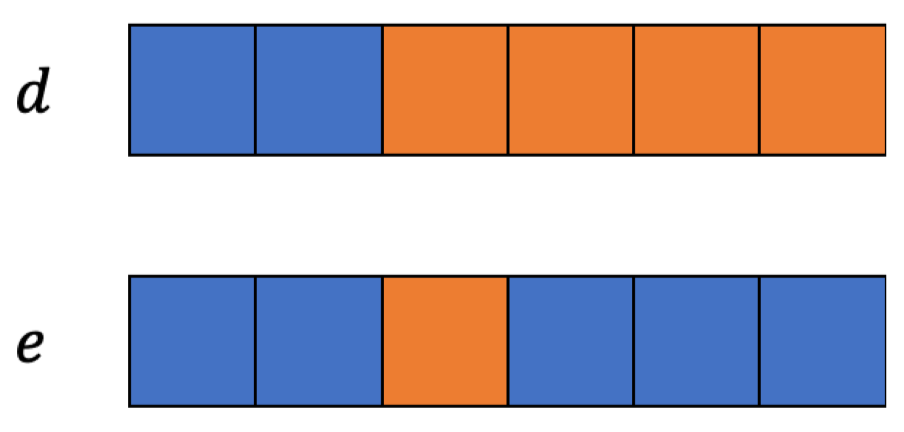
比特串𝑑是从𝑐第一位1出现起，之后都为1。比特串𝑒是除了𝑐第一位1出现的位置为1，其余位都为0。即成功将𝑐中第一位出现1的位置提取了出来。在上面的例子中，𝑑和𝑒用图形表示为：

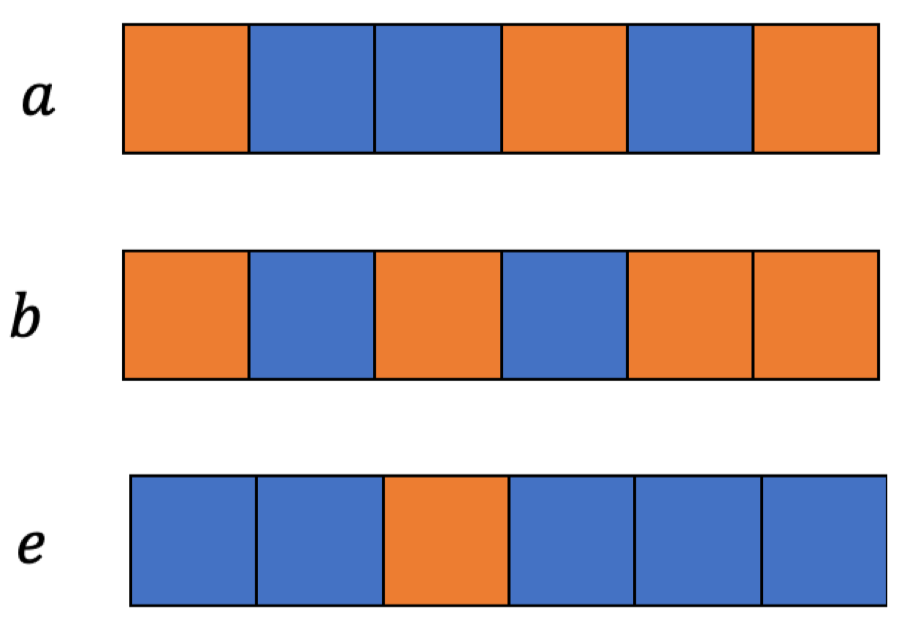
现在比特串𝑒中1的位置即为𝑐中第一位出现1的位置，将𝑐和𝑏进行按位与，如果𝑏第一位出现1的位置和𝑒中1的位置相同，那么该位按位与的结果就是1，其余位均为0，所有位相与结果之和就是1。反之，𝑏第一位出现1的位置和𝑒中1的位置不同，则为0。

将上述比较方式中的𝑎, 𝑏的各个比特都采用比特分享的方式进行分享，后续的「异或」以及「或」操作都采用我们之前介绍过的对子秘密的「比特异或」和「比特或」操作，即可实现对𝑎,𝑏的多方比较，且不向任何参与者泄露𝑎,𝑏的具体值。