来自今天的爱可可AI前沿推介
[LG] On a continuous time model of gradient descent dynamics and instability in deep learning
M Rosca, Y Wu, C Qin, B Dherin
[DeepMind & Google]
深度学习中梯度下降动力学和不稳定性的连续时间模型研究
要点:
-
提出关键流(PF),一种新的连续时间流,捕捉了深度学习中梯度下降动力学的行为; -
PF是第一个捕捉到梯度下降的发散和振荡行为的连续时间流,包括摆脱局部最小值和鞍点; -
通过对Hessian的特征分解的依赖,用PF来理解梯度下降的不稳定性。 -
提出一种学习率自适应方法,即漂移调整学习率(DAL),以控制深度学习中稳定性和性能之间的权衡。
一句话总结:
关键流(PF)是一种新的连续时间流,用来捕捉深度学习中的梯度下降动力学行为,提供了对不稳定性的洞察,并导致了控制稳定性和性能权衡的漂移调整学习率(DAL)的提出。
摘要:
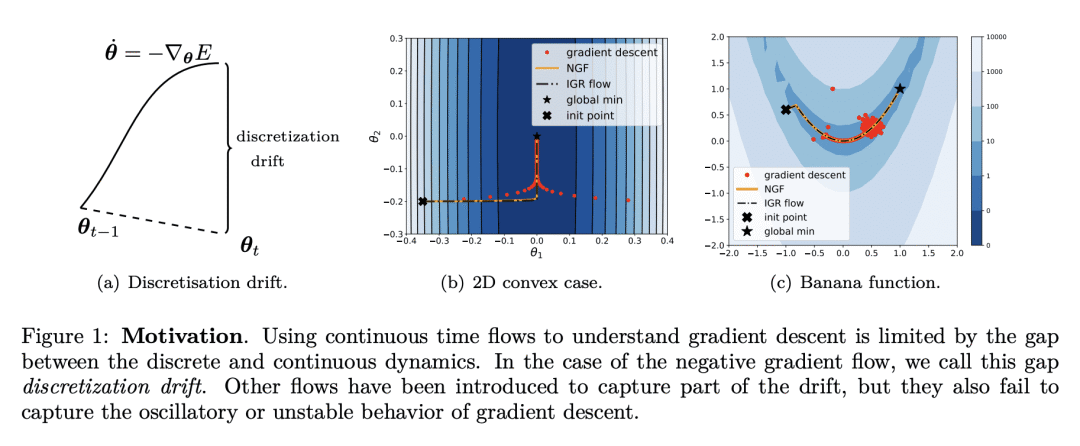
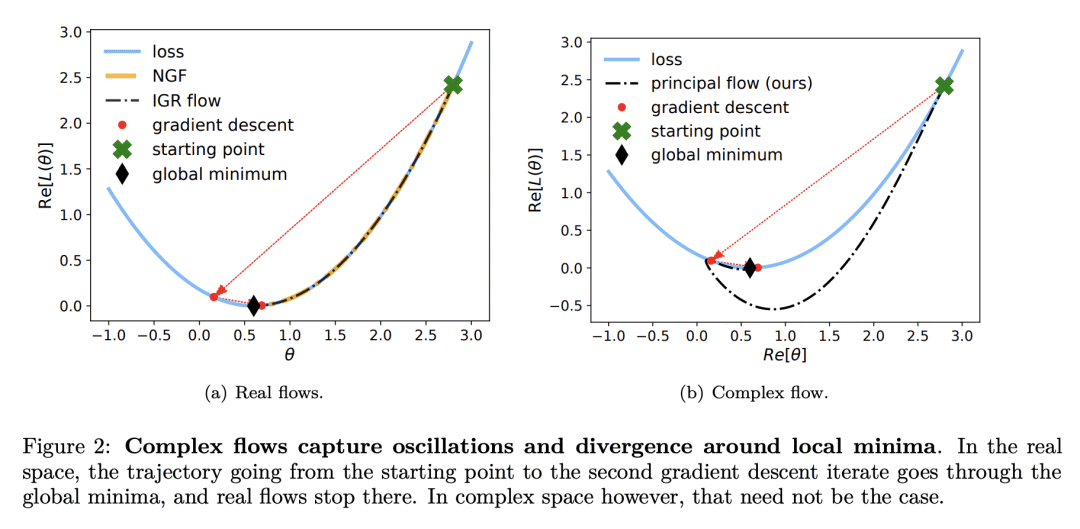
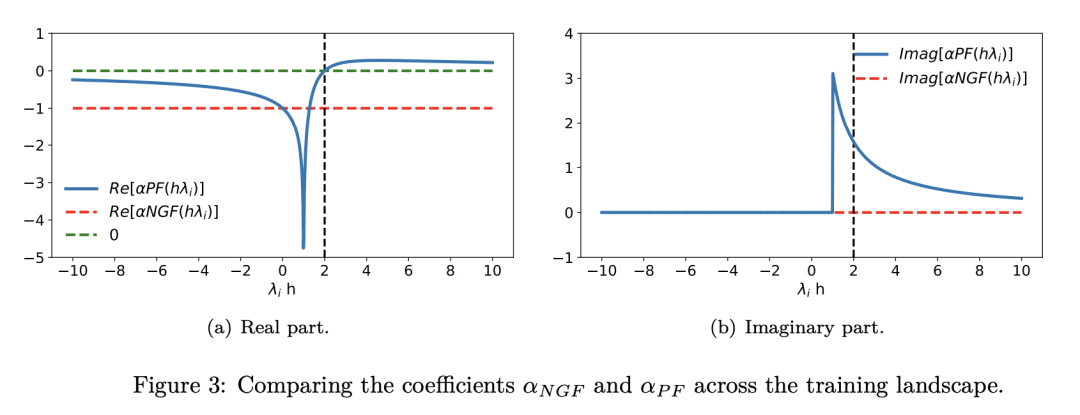
深度学习成功背后的秘诀是神经网络和基于梯度的优化的结合。然而,对梯度下降行为的理解,特别是其不稳定性,已经落后于其经验上的成功。为了增加研究梯度下降的理论工具,本文提出关键流(PF),一种接近梯度下降动力学的连续时间流。PF 是唯一能捕捉到梯度下降的发散和振荡行为的连续流,包括摆脱局部最小值和鞍点。通过它对Hessian的特征分解的依赖,PF 揭示了最近在深度学习中观察到的边缘稳定性现象。利用对不稳定性的新理解,本文提出一种学习率适应方法,使得能控制训练稳定性和测试集评估性能之间的权衡。
The recipe behind the success of deep learning has been the combination of neural networks and gradient-based optimization. Understanding the behavior of gradient descent however, and particularly its instability, has lagged behind its empirical success. To add to the theoretical tools available to study gradient descent we propose the principal flow (PF), a continuous time flow that approximates gradient descent dynamics. To our knowledge, the PF is the only continuous flow that captures the divergent and oscillatory behaviors of gradient descent, including escaping local minima and saddle points. Through its dependence on the eigendecomposition of the Hessian the PF sheds light on the recently observed edge of stability phenomena in deep learning. Using our new understanding of instability we propose a learning rate adaptation method which enables us to control the trade-off between training stability and test set evaluation performance.
论文链接:https://arxiv.org/abs/2302.01952
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢