来自今天的爱可可AI前沿推介
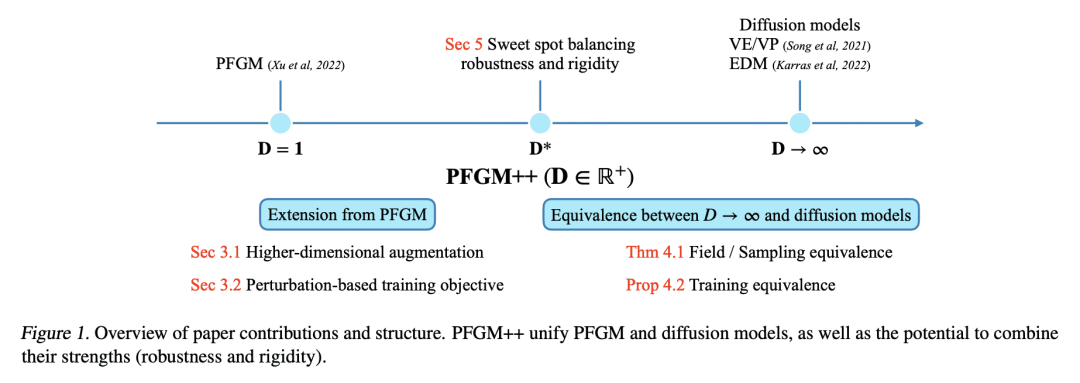
[LG] PFGM++: Unlocking the Potential of Physics-Inspired Generative Models
Y Xu, Z Liu, Y Tian, S Tong, M Tegmark, T Jaakkola
[MIT]
PFGM++: 释放物理学启发生成模型的潜力
要点:
-
提出 PFGM++,一个新的物理学启发的生成模型族,统一了扩散模型和泊松流生成模型(PFGM); -
一种基于扰动的目标,免除了任何有偏的大批量衍生电场目标,并允许无偏训练; -
通过改变D的值,证明了鲁棒性和刚性之间的权衡,经验结果表明,具有有限D的模型可以获得比扩散模型更好的性能,同时表现出更好的鲁棒性。
一句话总结:
提出一个新的物理学启发的生成模型族PFGM++,统一了扩散模型和泊松流生成模型,并证明它比之前最先进的扩散模型有更好的性能和鲁棒性。
摘要:
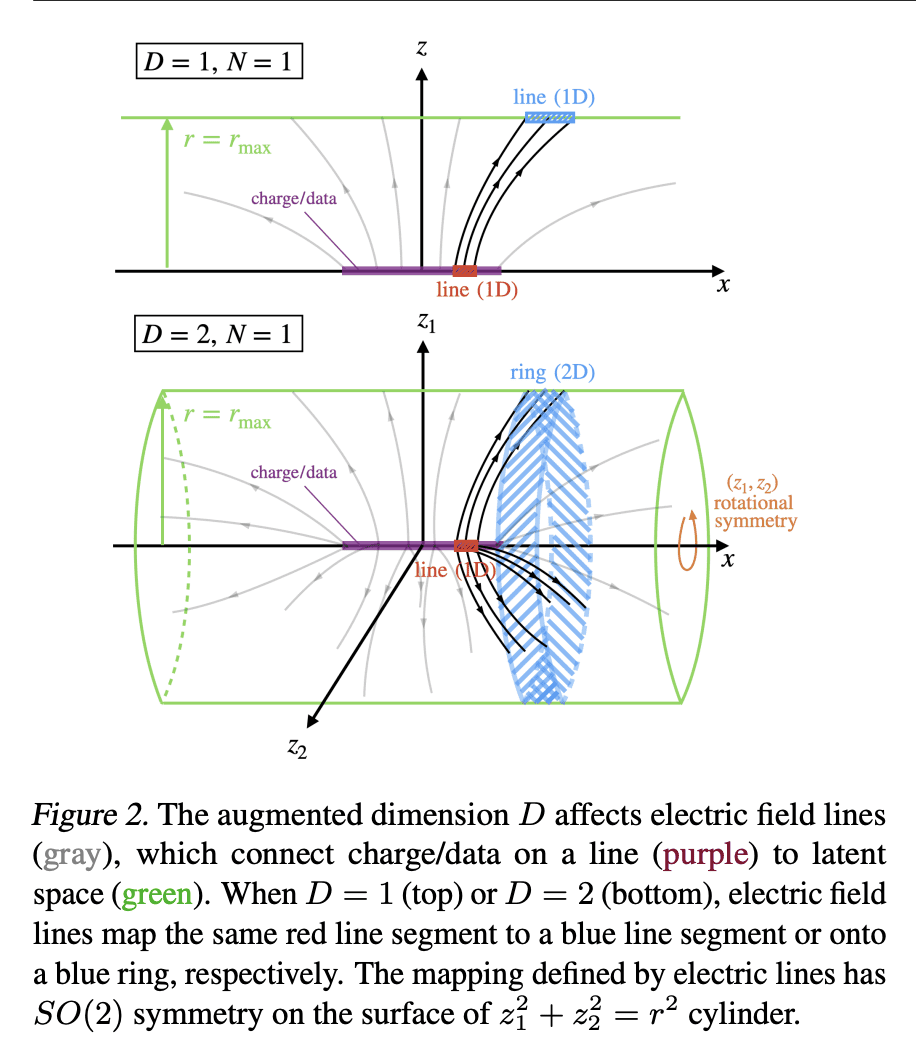
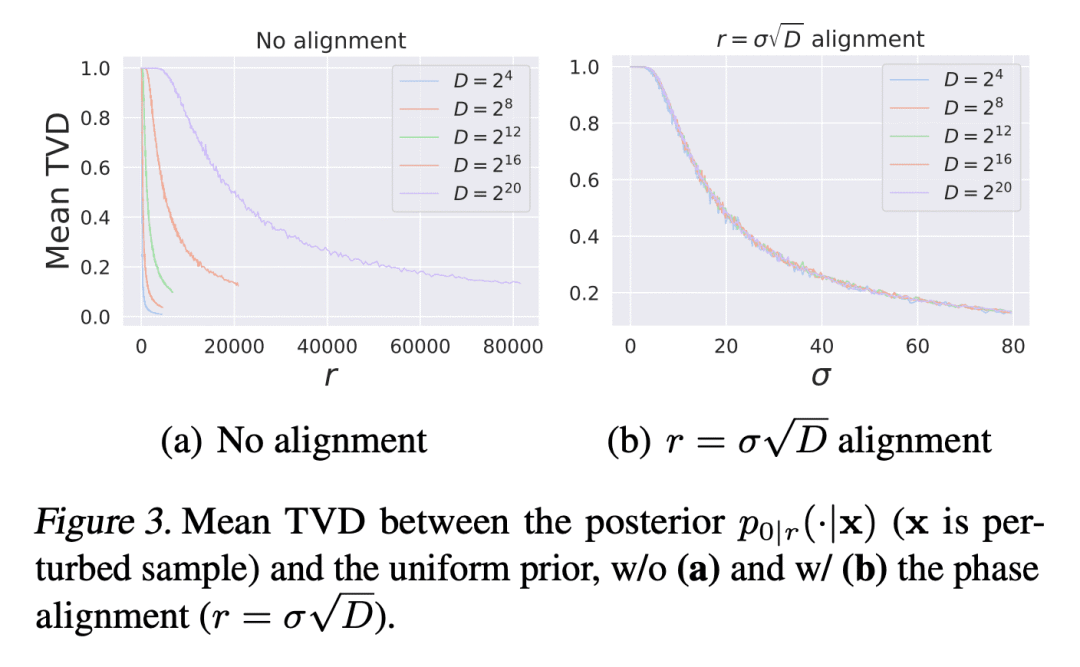
提出一个新的物理学启发的生成模型族——PFGM++,统一了扩散模型和泊松流生成模型(PFGM)。这些模型通过在 N+D 维空间中嵌入路径来实现 N 维数据的生成轨迹,同时仍然用 D 个额外变量的简单标量范数来控制进度。当 D=1 时,新模型还原为 PFGM,当 D→∞ 时还原为扩散模型。选择 D 的灵活性使得能权衡鲁棒性和刚性,因为增加 D 会使数据和附加变量准则之间的耦合更加集中。本文摒弃了 PFGM 中使用的有偏的大批量场目标,而是提供了一个类似于扩散模型的无偏的扰动目标。为了探索 D 的不同选择,本文提供了一种直接对齐的方法,将扩散模型(D→∞)的微调好的超参数迁移到任意有限的D值。实验表明,在 CIFAR-10/FFHQ 64×64 数据集上,有限D值的模型可以优于之前最先进的扩散模型,当 D=2048/128 时,FID 得分为 1.91/2.43。此外,本文证明了具有较小 D 的模型对建模错误表现出更好的鲁棒性。
We introduce a new family of physics-inspired generative models termed PFGM++ that unifies diffusion models and Poisson Flow Generative Models (PFGM). These models realize generative trajectories for N dimensional data by embedding paths in N+D dimensional space while still controlling the progression with a simple scalar norm of the D additional variables. The new models reduce to PFGM when D=1 and to diffusion models when D→∞. The flexibility of choosing D allows us to trade off robustness against rigidity as increasing D results in more concentrated coupling between the data and the additional variable norms. We dispense with the biased large batch field targets used in PFGM and instead provide an unbiased perturbation-based objective similar to diffusion models. To explore different choices of D, we provide a direct alignment method for transferring well-tuned hyperparameters from diffusion models (D→∞) to any finite D values. Our experiments show that models with finite D can be superior to previous state-of-the-art diffusion models on CIFAR-10/FFHQ 64×64 datasets, with FID scores of 1.91/2.43 when D=2048/128. In addition, we demonstrate that models with smaller D exhibit improved robustness against modeling errors. Code is available at this https URL
论文链接:https://arxiv.org/abs/2302.04265
 .
.
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢