【隐私计算笔谈】MPC系列专题（十三）：比特分解

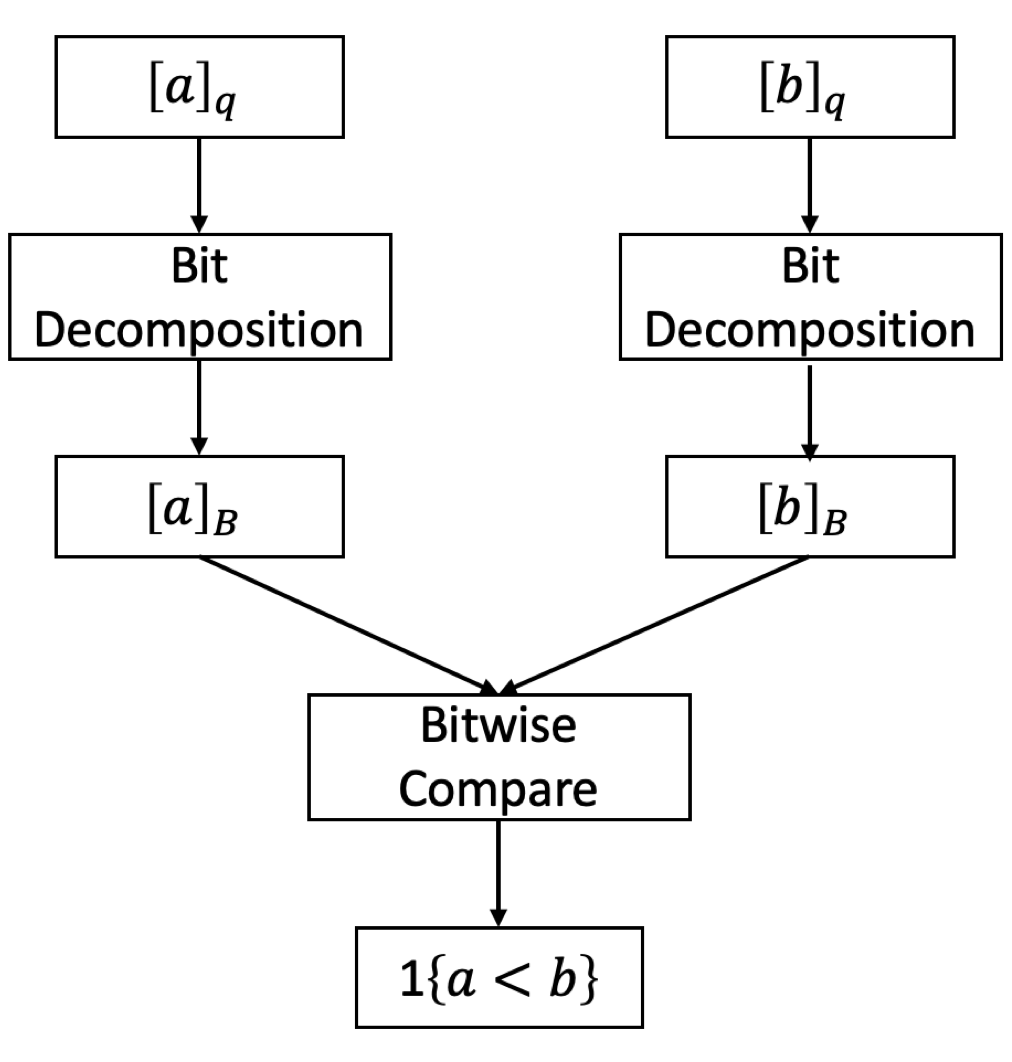
上一次科普介绍了比特比较(Bitwise Compare)，比特比较可以实现多方下的比较，不过其要求比较的输入是按比特分享的。回忆一下，在Shamir(t,n)秘密分享机制中所有被分享的秘密都是一个完整的比特串的形式，通过一个秘密多项式被分享成𝑛个在域𝐹_𝑞上的子秘密。

那么要想在Shamir(t,n)秘密分享机制中使用bitwise compare来实现多方比较，就需要将在域𝐹_𝑞上的子秘密以比特形式重新分享，将其记为[𝑎]_𝑝→[𝑎]_B，称为比特分解(Bit Decomposition)。

如果已经有了[𝑎]_B，将[𝑎]_B转换成[𝑎]_𝑝较为简单，因为[𝑎]_B={[𝑎₀]_B,…[𝑎_l-1]_B}，[𝑎_𝑖​]_B分别表示𝑎从高位数起按比特分享的第𝑖比特。由于

回忆一下Shamir(t, n)秘密共享机制的性质，所有对应的子秘密相加，等于主秘密相加；所有子秘密乘上同一个常数，等于主秘密乘上该常数。因此将[𝑎]_B→[𝑎]_𝑝只需计算。 

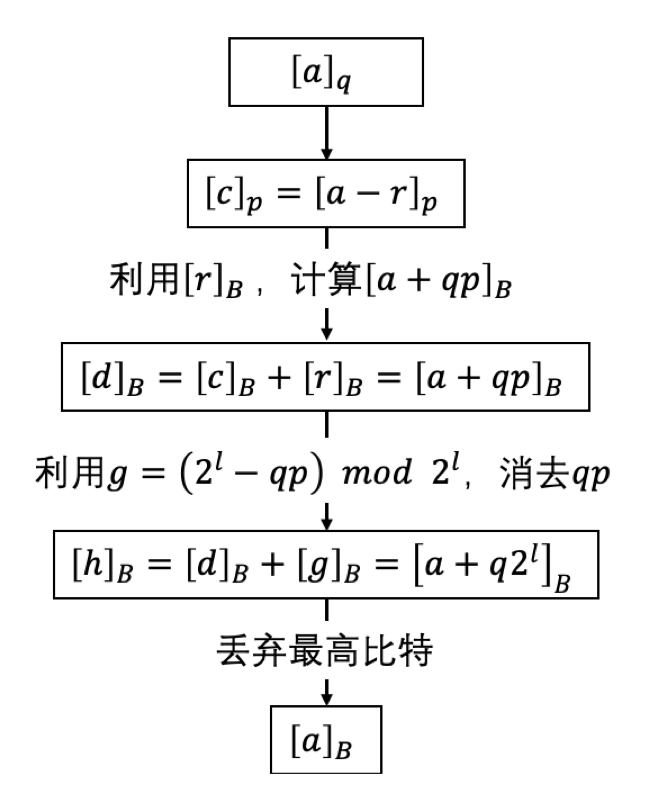
图:Bit Decomposition

比特分解(Bit Decomposition)[𝑎]_𝑝→[𝑎]_B的主要步骤为： 

1. 所有参与者共同产生一个随机数[𝑟]_B(上次科普介绍过如何共同产生随机数)，并计算对应的[𝑟]_𝑝。

2. 每个参与者都计算[𝑐]_𝑝=[𝑎]_𝑝−[𝑟]_𝑝，并将[𝑐]_𝑝进行公开。因此每个参与者都能获得𝑐=𝑎−𝑟 𝑚𝑜𝑑 𝑝。

3. 由于每个参与者都知道明文的𝑐，因此每个参与者都可计算 [𝑐]_B，之后 计算[𝑑]_B=[𝑟]_B+[𝑐]_B= {[𝑑₀]𝑝,…,[𝑑_𝑙]𝑝}。（注意这里用的加法是Bit-Add，[𝑑=𝑟+𝑐]_B，并不是直接按比特相加，同理下面用到的类似形式的实际都为，因为:

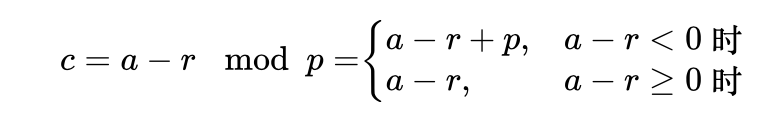
若此时对[𝑑]_B进行重构，获得的𝑑=𝑎+𝑞𝑝，𝑞∈ {0,1} ，因此[𝑑]_B的值其实是[𝑑]_B=[𝑎+𝑞𝑝]_B。现在需要想办法消去𝑞𝑝。𝑞的值可以使用上次科普介绍的比特比较（Bitwise Compare）协议，通过比较和得到，若𝑑<𝑝则𝑞=0，反之则𝑞=1。

4. 考虑=(2^𝑙−𝑞𝑝) 𝑚𝑜𝑑 2^𝑙，将它的按比特分享记为。将2^𝑙−𝑝的二进制表示记为𝑓₀⋯𝑓_𝑙-1，则

若将𝑞和2^𝑙−𝑝相乘后模上2^𝑙，可得到(2^𝑙−𝑝)𝑞 𝑚𝑜𝑑 2^𝑙=(2^𝑙𝑞−𝑝𝑞) 𝑚𝑜𝑑 2^𝑙=(2^𝑙−𝑝𝑞) 𝑚𝑜𝑑 2^𝑙=g。因此可以通过来计算。 

5. 现在有了和[𝑑]_B=[𝑎+𝑞𝑝]_B，可以通过将二者相加，获得。注意，𝑑是𝑙+1位的，而ℎ是𝑙位，二者相加后得到的最高位为，因此只要将最高位丢弃，那么留下的就是。有了比特分解之后，就可将[𝑎]_𝑝转换为[𝑎]_B，在通过上次科普介绍的Bitwise Compare(Less-Than)来进行多方比较。

​